Hostname: page-component-6bf8c574d5-vmclg Total loading time: 0 Render date: 2025-02-17T12:52:25.029Z Has data issue: false hasContentIssue false
  • English
  • Français

On the ergodicity of geodesic flows on surfaces without focal points

Part of: Ergodic theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  03 February 2023

WEISHENG WU ,
FEI LIU  and
FANG WANG
WEISHENG WU*
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen 361005, P. R. China
FEI LIU
Affiliation:
College of Mathematics and System Science, Shandong University of Science and Technology, Qingdao 266590, P. R. China (e-mail: [email protected])
FANG WANG
Affiliation:
School of Mathematical Sciences, Capital Normal University, Beijing 100048, China Beijing Center for Mathematics and Information Interdisciplinary Sciences (BCMIIS), Beijing 100048, P. R. China (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we study the ergodicity of the geodesic flows on surfaces with no focal points. Let M be a smooth connected and closed surface equipped with a 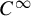$C^{\infty }$ Riemannian metric g, whose genus 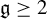$\mathfrak {g} \geq 2$. Suppose that 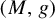$(M,g)$ has no focal points. We prove that the geodesic flow on the unit tangent bundle of M is ergodic with respect to the Liouville measure, under the assumption that the set of points on M with negative curvature has at most finitely many connected components.

Keywords

ergodicitygeodesic flowno focal pointsnon-uniform hyperbolicity

MSC classification

Primary: 37D40: Dynamical systems of geometric origin and hyperbolicity (geodesic and horocycle flows, etc.)
Secondary: 37A25: Ergodicity, mixing, rates of mixing 37D25: Nonuniformly hyperbolic systems (Lyapunov exponents, Pesin theory, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 12 , December 2023 , pp. 4226 - 4248
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anosov, D. V.. Geodesic flows on closed Riemannian manifolds with negative curvature. Proc. Steklov Inst. Math. 90 (1967), 1–235.Google Scholar
Anosov, D. V. and Sinai, Y. G.. Some smooth ergodic systems. Russian Math. Surveys 22(5) (1967), 103–168.CrossRefGoogle Scholar
Ballmann, W.. Lectures on Spaces of Nonpositive Curvature (DMV Seminar, 25). Birkhauser Verlag, Basel, 1995 (with an appendix by M. Brin).CrossRefGoogle Scholar
Ballmann, W., Brin, M. and Eberlein, P.. Structure of manifolds of nonpositive curvature. I. Ann. of Math. (2) 122 (1985), 171–203.CrossRefGoogle Scholar
Barreira, L. and Pesin, Y. B.. Nonuniform Hyperbolicity: Dynamics of Systems with Nonzero Lyapunov Exponents (Encyclopedia of Mathematics and Its Applications, 115). Cambridge University Press, Cambridge, 2007.CrossRefGoogle Scholar
Burago, D. and Ivanov, S.. Riemannian tori without conjugate points are flat. Geom. Funct. Anal. 4 (1994), 259–269.CrossRefGoogle Scholar
Burns, K. and Gelfert, K.. Lyapunov spectrum for geodesic flows of rank 1 surfaces. Discrete Contin. Dyn. Syst. 34 (2014), 1841–1872.10.3934/dcds.2014.34.1841CrossRefGoogle Scholar
Burns, K. and Matveev, V. S.. Open problems and questions about geodesics. Ergod. Th. & Dynam. Sys. 41(3) (2021), 641–684.CrossRefGoogle Scholar
Cao, J. and Xavier, F.. A closing lemma for flat strips in compact surfaces of non-positive curvature. Preprint, 2008.Google Scholar
Chen, D., Kao, L. and Park, K.. Unique equilibrium states for geodesic flows over surfaces without focal points. Nonlinearity 33(3) (2020), 1118–1155.CrossRefGoogle Scholar
Coudène, Y. and Schapira, B.. Generic measures for geodesic flows on nonpositively curved manifolds. J. Éc. polytech. Math. 1 (2014), 387–408.CrossRefGoogle Scholar
Eberlein, P.. When is a geodesic flow of Anosov type? I. J. Differential Geometry 8 (1973), 437–463.Google Scholar
Eberlein, P. and O’Neill, B.. Visibility manifolds. Pacific J. Math. 46(1) (1973), 45–109.CrossRefGoogle Scholar
Green, L. W.. Surfaces without conjugate points. Trans. Amer. Math. Soc. 76(3) (1954), 529–546.CrossRefGoogle Scholar
Gromov, M.. Manifolds of negative curvature. J. Differential Geometry 13 (1978), 223–230.CrossRefGoogle Scholar
Hopf, E.. Statistik der geodätischen Linien in Mannigfaltigkeiten negativer Krümmung. Ber. Verh. Sächs. Akad. Wiss. Leipzig 91 (1939), 261–304.Google Scholar
Hopf, E.. Statistik der Lösungen geodätischer Probleme vom unstabilen Typus. II. Math. Ann. 117 (1940), 590–608.CrossRefGoogle Scholar
Hopf, E.. Closed surfaces without conjugate points. Proc. Natl Acad. Sci. USA 34 (1948), 47–51.CrossRefGoogle ScholarPubMed
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and Its Applications, 54). Cambridge University Press, Cambridge, 1997.Google Scholar
Knieper, G.. The uniqueness of the measure of maximal entropy for geodesic flows on rank 1 manifolds. Ann. of Math. (2) 148 (1998), 291–314.CrossRefGoogle Scholar
O’Sullivan, J. J.. Riemannian manifolds without focal points. J. Differential Geom. 11 (1976), 321–333.Google Scholar
Rodriguez Hertz, F.. On the geodesic flow of surfaces of nonpositive curvature. Preprint, 2003, arXiv:math/0301010.Google Scholar
Ruggiero, R.. Flatness of Gaussian curvature and area of ideal triangles. Bull. Braz. Math. Soc. (N.S.) 28(1) (1997), 73–87.CrossRefGoogle Scholar
Watkins, J.. The higher rank rigidity theorem for manifolds with no focal points. Geom. Dedicata 164 (2013), 319–349.CrossRefGoogle Scholar
Wu, W.. On the ergodicity of geodesic flows on surfaces of nonpositive curvature. Ann. Fac. Sci. Toulouse Math. (6) 24(3) (2015), 625–639.CrossRefGoogle Scholar