Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T22:24:10.451Z Has data issue: false hasContentIssue false
  • English
  • Français

On the almost everywhere convergence of the ergodic averages†

Published online by Cambridge University Press:  19 September 2008

F. J. Martín-Reyes  and
A. De La Torre
F. J. Martín-Reyes
Affiliation:
Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, 29071-Málaga, Spain
A. De La Torre
Affiliation:
Análisis Matemático, Facultad de Ciencias, Universidad de Málaga, 29071-Málaga, Spain
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X, 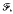ν) be a finite measure space and let T: X → X be a measurable transformation. In this paper we prove that the averages 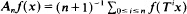converge a.e. for every f in Lp(dν), 1 < p < ∞, if and only if there exists a measure γ equivalent to ν such that the averages apply uniformly Lp(dν) into weak-Lp(dγ). As a corollary, we get that uniform boundedness of the averages in Lp(dν) implies a.e. convergence of the averages (a result recently obtained by Assani). In order to do this, we first study measures v equivalent to a finite invariant measure μ, and we prove that supn≥0An(dν/dμ)−1/(p−1) a.e. is a necessary and sufficient condition for the averages to converge a.e. for every f in Lp(dν).

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 10 , Issue 1 , March 1990 , pp. 141 - 149
Copyright
Copyright © Cambridge University Press 1990

References

REFERENCES

[1]Assani, I.. Quelques resultats sur les opérateurs positifs à moyennes bornées dan Lp. Ann. Scien. Clermont-Ferrand 85, Probabilités, Fasc. 3 (1985), 65–72.Google Scholar
[2]García-Cuerva, J. & Rubio de Francia, J. L.. Weighted Norm Inequalities and Related Topics. North Holland: Amsterdam, 1985.Google Scholar
[3]de Guzmán, M.. Real Variable Methods in Fourier Analysis. North-Holland: Amsterdam, 1981.Google Scholar
[4]Krengel, U.. Ergodic Theorems. Walter de Gruyter: 1985.CrossRefGoogle Scholar
[5]Martin-Reyes, F. J.. Inequalities for the maximal function and convergence of the averages in weighted Lp-spaces. Trans. Amer. Math. Soc. 296 (1986), 61–82.Google Scholar
[6]Martin-Reyes, F. J., Salvador, P. Ortega & de la Torre, A.. Weighted inequalities for one-sided maximal functions. To appear in T.A.M.S.Google Scholar
[7]Martin-Reyes, F. J. & de la Torre, A.. Weighted weak type inequalities for the ergodic maximal function and the pointwise ergodic theorem. Studia Math. 87 (1987), 33–46.Google Scholar
[8]Martin-Reyes, F. J. & de la Torre, A.. The dominated ergodic estimate for mean bounded, invertible, positive operators. Proc. Amer. Math. Soc. 104 (1988) 69–75.CrossRefGoogle Scholar
[9]Parry, W.. Topics in Ergodic Theory. Cambridge University Press: Cambridge, 1981.Google Scholar
[10]Sadosky, C.. Interpolation of Operators and Singular Integrals. Marcel Dekker: New York, 1979.Google Scholar
[11]Sato, R.. On a ratio ergodic theorem. Studia Math. 87 (1987), 47–52.CrossRefGoogle Scholar
[12]Sawyer, E.. Weighted inequalities for the one-sided Hardy Littlewood maximal functions. Trans. Amer. Math. Soc. 297 (1986), 53–61.CrossRefGoogle Scholar