Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T17:37:09.523Z Has data issue: false hasContentIssue false
  • English
  • Français

On preimage entropy, folding entropy and stable entropy

Part of: Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  14 January 2020

WEISHENG WU  and
YUJUN ZHU
WEISHENG WU
Affiliation:
Department of Applied Mathematics, Science College, China Agricultural University, Beijing100083, P.R. China email [email protected]
YUJUN ZHU
Affiliation:
School of Mathematical Sciences, Xiamen University, Xiamen361005, P.R. China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For non-invertible dynamical systems, we investigate how ‘non-invertible’ a system is and how the ‘non-invertibility’ contributes to the entropy from different viewpoints. For a continuous map on a compact metric space, we propose a notion of pointwise metric preimage entropy for invariant measures. For systems with uniform separation of preimages, we establish a variational principle between this version of pointwise metric preimage entropy and pointwise topological entropies introduced by Hurley [On topological entropy of maps. Ergod. Th. & Dynam. Sys.15 (1995), 557–568], which answers a question considered by Cheng and Newhouse [Pre-image entropy. Ergod. Th. & Dynam. Sys.25 (2005), 1091–1113]. Under the same condition, the notion coincides with folding entropy introduced by Ruelle [Positivity of entropy production in nonequilibrium statistical mechanics. J. Stat. Phys.85(1–2) (1996), 1–23]. For a 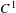$C^{1}$-partially hyperbolic (non-invertible and non-degenerate) endomorphism on a closed manifold, we introduce notions of stable topological and metric entropies, and establish a variational principle relating them. For 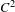$C^{2}$ systems, the stable metric entropy is expressed in terms of folding entropy (namely, pointwise metric preimage entropy) and negative Lyapunov exponents. Preimage entropy could be regarded as a special type of stable entropy when each stable manifold consists of a single point. Moreover, we also consider the upper semi-continuity for both of pointwise metric preimage entropy and stable entropy and give a version of the Shannon–McMillan–Breiman theorem for them.

Keywords

preimage entropyfolding entropystable entropyShannon–Breiman–McMillan theoremvariational principle

MSC classification

Primary: 37D35: Thermodynamic formalism, variational principles, equilibrium states
Secondary: 37D30: Partially hyperbolic systems and dominated splittings
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 4 , April 2021 , pp. 1217 - 1249
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bobok, J. and Nitecki, Z.. Topological entropy of m-fold maps. Ergod. Th. & Dynam. Sys. 25 (2005), 375–401.10.1017/S0143385704000574CrossRefGoogle Scholar
Cheng, W.-C. and Newhouse, S.. Pre-image entropy. Ergod. Th. & Dynam. Sys. 25 (2005), 1091–1113.10.1017/S0143385704000240CrossRefGoogle Scholar
Downarowicz, T.. Entropy in Dynamical Systems (New Mathematical Monographs, 18) . Cambridge University Press, Cambridge, 2011.10.1017/CBO9780511976155CrossRefGoogle Scholar
Fiebig, D., Fiebig, U. and Nitecki, Z.. Entropy and preimage sets. Ergod. Th. & Dynam. Sys. 23 (2003), 1785–1806.CrossRefGoogle Scholar
Hu, H., Hua, Y. and Wu, W.. Unstable entropies and variational principle for partially hyperbolic diffeomorphsims. Adv. Math. 321 (2017), 31–68.10.1016/j.aim.2017.09.039CrossRefGoogle Scholar
Hurley, M.. On topological entropy of maps. Ergod. Th. & Dynam. Sys. 15 (1995), 557–568.10.1017/S014338570000852XCrossRefGoogle Scholar
Langevin, R. and Przytycki, F.. Entropie de l’image inverse d’une application. Bull. Soc. Math. France 120 (1992), 237–250.10.24033/bsmf.2185CrossRefGoogle Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms: part I: Characterization of measures satisfying Pesin’s entropy formula. Ann. of Math. (2) 122 (1985), 509–539.Google Scholar
Ledrappier, F. and Young, L.-S.. The metric entropy of diffeomorphisms: part II: Relations between entropy, exponents and dimension. Ann. of Math. (2) 122 (1985), 540–574.Google Scholar
Liao, G. and Wang, S.. Ruelle inequality of folding type for C 1+𝛼 maps. Math. Z. 290(1–2) (2018), 509–519.CrossRefGoogle Scholar
Liu, P.-D.. Ruelle inequality relating entropy, folding entropy and negative Lyapunov exponents. Commun. Math. Phys. 240(3) (2003), 531–538.10.1007/s00220-003-0908-3CrossRefGoogle Scholar
Liu, P.-D.. Invariant measures satisfying an equality relating entropy, folding entropy and negative Lyapunov exponents. Commun. Math. Phys. 284(2) (2008), 391–406.CrossRefGoogle Scholar
Nitecki, Z. and Przytycki, F.. Preimage entropy for mappings. Internat. J. Bifur. Chaos 9 (1999), 1815–1843.10.1142/S0218127499001309CrossRefGoogle Scholar
Nitecki, Z.. Topological entropy and the preimage structure of maps. Real Anal. Exchange 29 (2003/2004), 7–39.Google Scholar
Qian, M., Xie, J.-S. and Zhu, S.. Smooth Ergodic Theory for Endomorphisms. Springer, Berlin, 2009.CrossRefGoogle Scholar
Rokhlin, V. A.. On the fundamental ideas of measure theory. Amer. Math. Soc. Transl. 1 (1962), 107–150.Google Scholar
Ruelle, D.. Positivity of entropy production in nonequilibrium statistical mechanics. J. Stat. Phys. 85(1–2) (1996), 1–23.CrossRefGoogle Scholar
Shu, L.. The metric entropy of endomorphisms. Commun. Math. Phys. 291(2) (2009), 491–512.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer, New York, 1982.10.1007/978-1-4612-5775-2CrossRefGoogle Scholar