Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T03:54:21.306Z Has data issue: false hasContentIssue false
  • English
  • Français

On nilspace systems and their morphisms

Part of: Connections with other structures, applications Topological dynamics

Published online by Cambridge University Press:  10 April 2019

PABLO CANDELA ,
DIEGO GONZÁLEZ-SÁNCHEZ  and
BALÁZS SZEGEDY
PABLO CANDELA
Affiliation:
Universidad Autónoma de Madrid and ICMAT, Ciudad Universitaria de Cantoblanco, Madrid28049, Spain email [email protected]
DIEGO GONZÁLEZ-SÁNCHEZ
Affiliation:
Universidad Autónoma de Madrid and ICMAT, Ciudad Universitaria de Cantoblanco, Madrid28049, Spain email [email protected]
BALÁZS SZEGEDY
Affiliation:
MTA Alfréd Rényi Institute of Mathematics, Reáltanoda utca 13–15, Budapest1053, Hungary email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A nilspace system is a generalization of a nilsystem, consisting of a compact nilspace 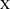$\text{X}$ equipped with a group of nilspace translations acting on 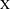$\text{X}$. Nilspace systems appear in different guises in several recent works and this motivates the study of these systems per se as well as their relation to more classical types of systems. In this paper we study morphisms of nilspace systems, i.e., nilspace morphisms with the additional property of being consistent with the actions of the given translations. A nilspace morphism does not necessarily have this property, but one of our main results shows that it factors through some other morphism which does have the property. As an application we obtain a strengthening of the inverse limit theorem for compact nilspaces, valid for nilspace systems. This is used in work of the first- and third-named authors to generalize the celebrated structure theorem of Host and Kra on characteristic factors.

Keywords

compact nilspacesnilspace systemsnilsystemsmorphisms

MSC classification

Primary: 37B99: None of the above, but in this section
Secondary: 54H20: Topological dynamics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 11 , November 2020 , pp. 3015 - 3029
Check for updates
Copyright
© Cambridge University Press, 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, L., Green, L. and Hahn, F.. Flows on Homogeneous Spaces (Annals of Mathematics Studies, 53) . Princeton University Press, Princeton, NJ, 1963.CrossRefGoogle Scholar
Camarena, O. A. and Szegedy, B.. Nilspaces, nilmanifolds and their morphisms. Preprint, 2010, arXiv:1009.3825.Google Scholar
Candela, P.. Notes on nilspaces: algebraic aspects. Discrete Analysis (2017), Paper No. 15, 59 pp.Google Scholar
Candela, P.. Notes on compact nilspaces. Discrete Analysis (2017), Paper No. 16, 57 pp.Google Scholar
Candela, P. and Szegedy, B.. Nilspace factors for general uniformity seminorms, cubic exchangeability and limits. Preprint, 2018, arXiv:1803.08758.Google Scholar
Furstenberg, H.. Strict ergodicity and transformation of the torus. Amer. J. Math. 83 (1961), 573–601.CrossRefGoogle Scholar
Glasner, E., Gutman, Y. and Ye, X.. Higher order regionally proximal equivalence relations for general minimal group actions. Adv. Math. 333 (2018), 1004–1041.CrossRefGoogle Scholar
Gutman, Y., Manners, F. and Varjú, P. P.. The structure theory of nilspaces I. J. Anal. Math. to appear.Google Scholar
Gutman, Y., Manners, F. and Varjú, P. P.. The structure theory of nilspaces II: representation as nilmanifolds. Trans. Amer. Math. Soc. (2018), published online 1 October 2018.CrossRefGoogle Scholar
Gutman, Y., Manners, F. and Varjú, P. P.. The structure theory of nilspaces III: inverse limit representations and topological dynamics. Preprint, 2016, arXiv:1605.08950.Google Scholar
Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 397–488.CrossRefGoogle Scholar
Host, B. and Kra, B.. Nilpotent Structures in Ergodic Theory (Mathematical Surveys and Monographs, 236) . American Mathematical Society, Providence, RI, 2018.CrossRefGoogle Scholar
Host, B., Kra, B. and Maass, A.. Nilsequences and a structure theorem for topological dynamical systems. Adv. Math. 224(1) (2010), 103–129.CrossRefGoogle Scholar
Mal’cev, A. I.. On a class of homogeneous spaces. Izv. Akad. Nauk SSSR Ser. Mat. 13 (1949), 9–32.Google Scholar
Munkres, J. R.. Topology, 2nd edn. Prentice Hall, Upper Saddle River, NJ, 2000.Google Scholar
Parry, W.. Ergodic properties of affine transformations and flows on nilmanifolds. Amer. J. Math. 91 (1969), 757–771.CrossRefGoogle Scholar
Ziegler, T.. Universal characteristic factors and Furstenberg averages. J. Amer. Math. Soc. 20(1) (2007), 53–97.CrossRefGoogle Scholar