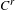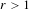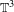Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Vásquez, Carlos H.
and
Andersson, Martin
2020.
Statistical stability of mostly expanding diffeomorphisms.
Annales de l'Institut Henri Poincaré C, Analyse non linéaire,
Vol. 37,
Issue. 6,
p.
1245.
Mi, Zeya
and
Cao, Yongluo
2021.
Statistical stability for diffeomorphisms with mostly expanding and mostly contracting centers.
Mathematische Zeitschrift,
Vol. 299,
Issue. 3-4,
p.
2519.
Gan, Shaobo
Yang, Fan
Yang, Jiagang
and
Zheng, Rusong
2021.
Statistical properties of physical-like measures*.
Nonlinearity,
Vol. 34,
Issue. 2,
p.
1014.
Gan, Shaobo
Li, Ming
Viana, Marcelo
and
Yang, Jiagang
2021.
Partially volume expanding diffeomorphisms.
Annales Henri Poincaré,
Vol. 22,
Issue. 1,
p.
331.
Yang, Jiagang
2021.
Entropy along expanding foliations.
Advances in Mathematics,
Vol. 389,
Issue. ,
p.
107893.
Mi, Zeya
2021.
Physical measures for partially hyperbolic flows with mostly contracting centre.
Dynamical Systems,
Vol. 36,
Issue. 3,
p.
427.
Rodriguez Hertz, Jana
Ures, Raúl
and
Yang, Jiagang
2022.
Robust minimality of strong foliations for DA diffeomorphisms: 𝑐𝑢-volume expansion and new examples.
Transactions of the American Mathematical Society,
Vol. 375,
Issue. 6,
p.
4333.
Yang, Jiagang
2023.
GEOMETRICAL AND MEASURE-THEORETIC STRUCTURES OF MAPS WITH A MOSTLY EXPANDING CENTER.
Journal of the Institute of Mathematics of Jussieu,
Vol. 22,
Issue. 2,
p.
919.
Mi, Zeya
2023.
Stochastic stability for partially hyperbolic diffeomorphisms with mostly expanding and mostly contracting centers.
Stochastics and Dynamics,
Vol. 23,
Issue. 04,
Cao, Yongluo
Mi, Zeya
and
Yang, Jiagang
2024.
Physical measures for partially hyperbolic diffeomorphisms with mixed hyperbolicity
*
.
Nonlinearity,
Vol. 37,
Issue. 7,
p.
075005.
Mi, Zeya
You, Biao
and
Zang, Yuntao
2024.
SRB Measures for Partially Hyperbolic Flows with Mostly Expanding Center.
Journal of Dynamics and Differential Equations,
Vol. 36,
Issue. 2,
p.
1153.
Mi, Zeya
Wang, Qiyuan
and
Cao, Yongluo
2024.
Physical measures under the hyperbolicity of pseudo-physical measures.
Journal of Differential Equations,
Vol. 400,
Issue. ,
p.
230.
Xiaobo, Hou
Wanshan, Lin
and
Xueting, Tian
2025.
Topological entropy of the set of points without physical-like behaviour and away from measures satisfying the entropy formula beyond uniform hyperbolicity.
SCIENTIA SINICA Mathematica,