Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T04:08:45.007Z Has data issue: false hasContentIssue false
  • English
  • Français

On minimal self-joinings in topological dynamics

Published online by Cambridge University Press:  19 September 2008

Andrés del Junco
Andrés del Junco
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Canada, M5S 1A1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If X is a compact metric space and T a homeomorphism of X we say (X, T) has almost minimal power joinings (AMPJ) if there is a dense GδX* in X such that for each finite set k, x∈(X*)k and l:k → ℤ−{0}, the orbit closure cl {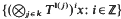} is a product of off-diagonals (POOD) on Xk. By an offdiagonal on Xk′, k′k we mean a set of the form (⊗,j∈k′Tm(j))Δ, Δ the diagonal in Xk′, m:k′→ℤ any function, and by a POOD on Xk we mean that k is split into subsets k′, on each Xk′ we put an off-diagonal and then we take the product of these.

We show that examples of AMPJ exist and that this definition leads to a theory completely analogous to Rudolph's theory of minimal self-joinings in ergodic theory. In particular if (X, T) has AMPJ the automorphism group of T is {Tn}, T has only almost 1-1 factors (other than the trivial one) and the automorphism group and factors of ⊕i ∊ kT, k finite or countably infinite, can be very explicitly described. We also discuss ℝ-actions.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 7 , Issue 2 , June 1987 , pp. 211 - 227
Copyright
Copyright © Cambridge University Press 1987

References

REFERENCES

[A, M]Auslander, J. & Markley, N.. Graphic minimal sets. Preprint.Google Scholar
[F, K, S]Furstenberg, H., Keynes, H. & Shapiro, L.. Prime flows in topological dynamics. Israel J. Math. 14 (1973), 26–38.CrossRefGoogle Scholar
[J]Junco, A. del. A family of counterexamples in ergodic theory. Israel J. Math. 44 (1983), 160–188.CrossRefGoogle Scholar
[J, K]Junco, A. del & Keane, M.. On generic points in the cartesian square of Chacón's transformation. To appear in Ergod. Th. & Dynam. Sys.Google Scholar
[J, P]Junco, A. del & Park, K.. An example of a measure-preserving flow with minimal self-joinings. J. d'Analyse Math. 42 (1983), 99–211.Google Scholar
[J, R]Junco, A. del & Rudolph, D.. On ergodic actions whose self-joinings are graphs. Preprint.Google Scholar
[J, R, S]Junco, A. del, Rahe, A. M. & Swanson, L.. Chacón's automorphism has minimal self-joinings. J. d'Analyse Math. 37 (1980), 276–284.CrossRefGoogle Scholar
[M]Markley, N.. Topological minimal self-joinings. Preprint.Google Scholar
[Ra]Ratner, M.. Joinings of horocycle flows. Preprint.Google Scholar
[Ru]Rudolph, D. R.. An example of a measure-preserving map with minimal self-joinings, and applications. J d'Analyse Math. 35 (1979), 97–122.CrossRefGoogle Scholar