Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-25T05:19:24.431Z Has data issue: false hasContentIssue false
  • English
  • Français

On factors of Gibbs measures for almost additive potentials

Published online by Cambridge University Press:  11 August 2014

YUKI YAYAMA
YUKI YAYAMA*
Affiliation:
Departamento de Ciencias Básicas, Universidad del Bío-Bío, Av. Andrés Bello, s/n Casilla 447 Chillán, Chile email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 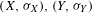$(X,{\it\sigma}_{X}),(Y,{\it\sigma}_{Y})$ be one-sided subshifts and 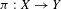${\it\pi}:X\rightarrow Y$ a factor map. Suppose that 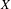$X$ has the specification property. Let 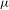${\it\mu}$ be a unique invariant Gibbs measure for a sequence of continuous functions 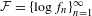${\mathcal{F}}=\{\log f_{n}\}_{n=1}^{\infty }$ on 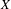$X$, which is an almost additive potential with bounded variation. We show that 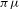${\it\pi}{\it\mu}$ is a unique invariant Gibbs measure for a sequence of continuous functions 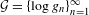${\mathcal{G}}=\{\log g_{n}\}_{n=1}^{\infty }$ on $Y$. When 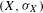$(X,{\it\sigma}_{X})$ is a full shift, we characterize 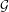${\mathcal{G}}$ and 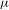${\it\mu}$ by using relative pressure. This 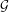${\mathcal{G}}$ is a generalization of a continuous function found by Pollicott and Kempton in their work on factors of Gibbs measures for continuous functions. We also consider the following question: given a unique invariant Gibbs measure ${\it\nu}$ for a sequence of continuous functions 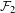${\mathcal{F}}_{2}$ on $Y$, can we find an invariant Gibbs measure 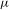${\it\mu}$ for a sequence of continuous functions 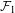${\mathcal{F}}_{1}$ on 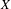$X$ such that 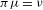${\it\pi}{\it\mu}={\it\nu}$? We show that such a measure exists under a certain condition. In particular, if 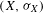$(X,{\it\sigma}_{X})$ is a full shift and ${\it\nu}$ is a unique invariant Gibbs measure for a function in the Bowen class, then there exists a preimage 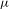${\it\mu}$ of ${\it\nu}$ which is a unique invariant Gibbs measure for a function in the Bowen class.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 1 , February 2016 , pp. 276 - 309
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allahbakhshi, M. and Quas, A.. Class degree and relative maximal entropy. Trans. Amer. Math. Soc. 365(3) (2013), 1347–1368.CrossRefGoogle Scholar
Barral, J. and Feng, D.-J.. Weighted thermodynamic formalism on subshifts and applications. Asian J. Math. 16(2) (2012), 319–352.CrossRefGoogle Scholar
Barreira, L.. Nonadditive thermodynamic formalism: equilibrium and Gibbs measures. Discrete Contin. Dyn. Syst. 16 (2006), 279–305.CrossRefGoogle Scholar
Bedford, T.. Crinkly curves, Markov partitions and box dimension in self-similar sets. PhD Thesis, University of Warwick, 1984.Google Scholar
Boyle, M. and Petersen, K.. Hidden Markov processes in the context of symbolic dynamics. Entropy of Hidden Markov Processes and Connections to Dynamical Systems (London Mathematical Society Lecture Note Series, 385). Eds. Marcus, B., Petersen, K. E. and Weissman, T.. Cambridge University Press, Cambridge, 2011, pp. 5–71.CrossRefGoogle Scholar
Boyle, M. and Tuncel, S.. Infinite-to-one codes and Markov measures. Trans. Amer. Math. Soc. 285 (1984), 657–684.CrossRefGoogle Scholar
Cao, Y.-L., Feng, D.-J. and Huang, W.. The thermodynamic formalism for sub-additive potentials. Discrete Contin. Dyn. Syst. 20 (2008), 639–657.CrossRefGoogle Scholar
Chazottes, J.-R. and Ugalde, E.. Projection of Markov measures may be Gibbsian. J. Stat. Phys. 111(5–6) (2003), 1245–1272.CrossRefGoogle Scholar
Chazottes, J.-R. and Ugalde, E.. On the preservation of Gibbsianness under symbol amalgamation. Entropy of Hidden Markov Processes and Connections to Dynamical Systems (London Mathematical Society Lecture Note Series, 385). Eds. Marcus, B., Petersen, K. E. and Weissman, T.. Cambridge University Press, Cambridge, 2011, pp. 72–97.CrossRefGoogle Scholar
van Enter, A.. Renormalization group, non-Gibbsian states, their relationship and further developments. Applications of Renormalization Group Methods in the Mathematical Sciences (RIMS Lecture Notes, 1482). Research Institute of Mathematical Sciences (RIMS), Kyoto University, Kyoto, Japan, 2006, pp. 49–64.Google Scholar
van Enter, A., Fernández, R. and Sokal, A.. Regularity properties and pathologies of position-space renormalization-group transformations: scope and limitations of Gibbsian theory. J. Stat. Phys. 72(5–6) (1993), 879–1167.CrossRefGoogle Scholar
Feng, D.-J.. Equilibrium states for factor maps between subshifts. Adv. Math. 226(3) (2011), 2470–2502.CrossRefGoogle Scholar
Feng, D.-J. and Huang, W.. Lyapunov spectrum of asymptotically sub-additive potentials. Comm. Math. Phys. 297(1) (2010), 1–43.CrossRefGoogle Scholar
Iommi, G. and Yayama, Y.. Almost-additive thermodynamic formalism for countable Markov shifts. Nonlinearity 25(1) (2012), 165–191.CrossRefGoogle Scholar
Kempton, T. M. W.. Factors of Gibbs measures for subshifts of finite type. Bull. Lond. Math. Soc. 43(4) (2011), 751–764.CrossRefGoogle Scholar
Kenyon, R. and Peres, Y.. Hausdorff dimensions of sofic affine-invariant sets. Israel J. Math. 94 (1996), 157–178.CrossRefGoogle Scholar
Kenyon, R. and Peres, Y.. Measures of full dimension on affine-invariant sets. Ergod. Th. & Dynam. Sys. 16 (1996), 307–323.CrossRefGoogle Scholar
Ledrappier, F. and Walters, P.. A relativised variational principle for continuous transformations. J. Lond. Math. Soc. (2) 16 (1977), 568–576.CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Maes, C., Redig, F. and van Moffaert, A.. Almost Gibbsian versus weakly Gibbsian measures. Stochastic Proccess. Appl. 79(1) (1999), 1–15.CrossRefGoogle Scholar
Marcus, B., Petersen, K. E. and Weissman, T.. Eds Entropy of Hidden Markov Processes and Connections to Dynamical Systems (London Mathematical Society Lecture Note Series, 385). Cambridge University Press, Cambridge, 2011.CrossRefGoogle Scholar
McMullen, C.. The Hausdorff dimension of general Sierpiński carpets. Nagoya Math. J. 96 (1984), 1–9.CrossRefGoogle Scholar
Mummert, A.. The thermodynamic formalism for almost-additive sequences. Discrete Contin. Dyn. Syst. 16 (2006), 435–454.CrossRefGoogle Scholar
Olivier, E.. Uniqueness of the measure with full dimension on sofic affine-invariant subsets of the 2-torus. Ergod. Th. & Dynam. Sys. 30(5) (2010), 1503–1528.CrossRefGoogle Scholar
Petersen, K., Quas, A. and Shin, S.. Measures of maximal relative entropy. Ergod. Th. & Dynam. Sys. 23 (2003), 207–223.CrossRefGoogle Scholar
Petersen, K. and Shin, S.. On the definition of relative pressure for factor maps on shifts of finite type. Bull. Lond. Math. Soc. 37 (2005), 601–612.CrossRefGoogle Scholar
Pollicott, M. and Kempton, T.. Factors of Gibbs measures for full shifts. Entropy of Hidden Markov Processes and Connections to Dynamical Systems (London Mathematical Society Lecture Note Series, 385). Eds. Marcus, B., Petersen, K. E. and Weissman, T.. Cambridge University Press, Cambridge, 2011, pp. 246–257.CrossRefGoogle Scholar
Verbitskiy, E.. On factors of g-measures. Indag. Math. (N.S.) 22(3–4) (2011), 315–329.CrossRefGoogle Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79). Springer-Verlag, New York, 1982.CrossRefGoogle Scholar
Walters, P.. Relative pressure, relative equilibrium states, compensation functions and many-to-one codes between subshifts. Trans. Amer. Math. Soc. 296 (1986), 1–31.CrossRefGoogle Scholar
Walters, P.. Regularity conditions and Bernoulli properties of equilibrium states and g-measures. J. Lond. Math. Soc. (2) 71 (2005), 379–396.CrossRefGoogle Scholar
Yayama, Y.. Dimensions of compact invariant sets of some expanding maps. Ergod. Th. & Dynam. Sys. 29(1) (2009), 281–315.CrossRefGoogle Scholar
Yayama, Y.. Existence of a measurable saturated compensation function between subshifts and its applications. Ergod. Th. & Dynam. Sys. 31(5) (2011), 1563–1589.CrossRefGoogle Scholar
Yayama, Y.. Applications of a relative variational principle to dimensions of nonconformal expanding maps. Stoch. Dyn. 11(4) (2011), 643–679.CrossRefGoogle Scholar
Yoo, J.. On factor maps that send Markov measures to Gibbs measures. J. Stat. Phys. 141(6) (2010), 1055–1070.CrossRefGoogle Scholar
Zhao, Y. and Cao, Y.. On the topological pressure of random bundle transformations in sub-additive case. J. Math. Anal. Appl. 342 (2008), 715–725.CrossRefGoogle Scholar
Zhao, Y. and Cao, Y.. Measure-theoretic pressure for subadditive potentials. Nonlinear Anal. 70(6) (2009), 2237–2247.CrossRefGoogle Scholar