Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
King, Jonathan L.
1988.
Joining-rank and the structure of finite rank mixing transformations.
Journal d'Analyse Mathématique,
Vol. 51,
Issue. 1,
p.
182.
Friedman, Nathaniel
Gabriel, Patrick
and
King, Jonathan
1988.
An invariant for rigid rank-1 transformations.
Ergodic Theory and Dynamical Systems,
Vol. 8,
Issue. 1,
p.
53.
Rudolph, Daniel J.
and
Silva, Cesar E.
1989.
Minimal self-joinings for nonsingular transformations.
Ergodic Theory and Dynamical Systems,
Vol. 9,
Issue. 4,
p.
759.
Lemańczyk, Mariusz
and
Mentzen, Mieczyslaw K.
1990.
Compact subgroups in the centralizer of natural factors of an ergodic group extension of a rotation determine all factors.
Ergodic Theory and Dynamical Systems,
Vol. 10,
Issue. 4,
p.
763.
Glasner, Eli
1990.
A topological version of a theorem of Veech and almost simple flows.
Ergodic Theory and Dynamical Systems,
Vol. 10,
Issue. 3,
p.
463.
Host, Bernard
1991.
Mixing of all orders and pairwise independent joinings of systems with singular spectrum.
Israel Journal of Mathematics,
Vol. 76,
Issue. 3,
p.
289.
Park, Kyewon K.
and
Robinson, E. Arthur
1991.
The joinings within a class of ℤ2 actions.
Journal d’Analyse Mathématique,
Vol. 57,
Issue. 1,
p.
1.
Ryzhikov, V. V.
1991.
Nonisomorphic full automorphism groups of nonseparable measure spaces.
Mathematical Notes of the Academy of Sciences of the USSR,
Vol. 50,
Issue. 4,
p.
1087.
King, Jonathan L.
and
Thouvenot, Jean-Paul
1991.
A canonical structure theorem for finite joining-rank maps.
Journal d'Analyse Mathématique,
Vol. 56,
Issue. 1,
p.
211.
Kwiatkowski, J.
Lemańczyk, M.
and
Rudolph, D.
1992.
Weak isomorphism of measure-preserving diffeomorphisms.
Israel Journal of Mathematics,
Vol. 80,
Issue. 1-2,
p.
33.
Glasner, E.
Host, B.
and
Rudolph, D.
1992.
Simple systems and their higher order self-joinings.
Israel Journal of Mathematics,
Vol. 78,
Issue. 1,
p.
131.
Park, Kyewon Koh
1992.
𝐺𝐿(2,𝑍) action on a two torus.
Proceedings of the American Mathematical Society,
Vol. 114,
Issue. 4,
p.
955.
King, Jonathan L.
1992.
Ergodic properties where order 4 implies infinite order.
Israel Journal of Mathematics,
Vol. 80,
Issue. 1-2,
p.
65.
Lemańczyk, Mariusz
Liardet, Pierre
and
Thouvenot, Jean-Paul
1992.
Coalescence of circle extensions of measure-preserving transformations.
Ergodic Theory and Dynamical Systems,
Vol. 12,
Issue. 4,
p.
769.
Ryzhikov, V. V.
1992.
Stochastic intertwinings and joinings of dynamic systems.
Mathematical Notes,
Vol. 52,
Issue. 3,
p.
971.
Ryzhikov, V. V.
1993.
Joinings and multiple mixing of finite rank actions.
Functional Analysis and Its Applications,
Vol. 27,
Issue. 2,
p.
128.
Fieldsteel, Adam
Del Junco, Andrés
and
Rudolph, Daniel J.
1994.
α-equivalence: a refinement of Kakutani equivalence.
Ergodic Theory and Dynamical Systems,
Vol. 14,
Issue. 1,
p.
69.
Goodson, Geoffrey R.
del Junco, Andrés
Lemańczyk, Mariusz
and
Rudolph, Daniel J.
1996.
Ergodic transformations conjugate to their inverses by involutions.
Ergodic Theory and Dynamical Systems,
Vol. 16,
Issue. 1,
p.
97.
Рыжиков, Валерий Валентинович
and
Ryzhikov, Valerii Valentinovich
1996.
Четная и нечетная простота динамических систем с инвариантной мерой.
Математические заметки,
Vol. 60,
Issue. 3,
p.
470.
Ryzhikov, V. V.
1996.
Stochastic intertwinings and multiple mixing of dynamical systems.
Journal of Dynamical and Control Systems,
Vol. 2,
Issue. 1,
p.
1.
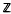 -action with minimal self-joinings are disjoint.
-action with minimal self-joinings are disjoint.

