Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-27T19:41:13.199Z Has data issue: false hasContentIssue false
  • English
  • Français

On embedding of repetitive Meyer multiple sets into model multiple sets

Published online by Cambridge University Press:  11 February 2015

JEAN-BAPTISTE AUJOGUE
JEAN-BAPTISTE AUJOGUE*
Affiliation:
Université de Lyon, CNRS UMR 5208, Université Lyon 1, Institut Camille Jordan, 43 blvd. du 11 novembre 1918, F-69622 Villeurbanne cedex, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Model sets are always Meyer sets but the converse is generally not true. In this work we show that for a repetitive Meyer multiple set of 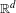$\mathbb{R}^{d}$ with associated dynamical system 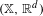$(\mathbb{X},\mathbb{R}^{d})$ , the property of being a model multiple set is equivalent to 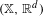$(\mathbb{X},\mathbb{R}^{d})$ being almost automorphic. We deduce this by showing that a repetitive Meyer multiple set can always be embedded into a repetitive model multiple set having a smaller group of topological eigenvalues.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 6 , September 2016 , pp. 1679 - 1702
Copyright
© Cambridge University Press, 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, J.. Minimal Flows and Their Extensions (Notas de Matemàtica, 153) . North-Holland Mathematics Studies, North-Holland, Amsterdam, 1988, http://books.google.fr/books?id=e3wFvPvpWvwC.Google Scholar
Baake, M., Hermisson, J. and Pleasant, P. A. B.. The torus parameterization of quasisperiodic LI-classes. J. Phys. A: Math. Gen. 30 (1997), 3029–3056.CrossRefGoogle Scholar
Baake, M. and Lenz, D.. Dynamical systems on translation bounded measures: pure point dynamical and diffraction spectra. Ergod. Th. & Dynam. Sys. 24(6) (2004), 1867–1893.Google Scholar
Baake, M., Lenz, D. and Moody, R. V.. Characterization of model sets by dynamical systems. Ergod. Th. & Dynam. Sys. 27(2) (2007), 341–382.Google Scholar
Baake, M., Lenz, D. and Richard, C.. Pure point diffraction implies zero entropy for Delone sets with uniform cluster frequencies. Lett. Math. Phys. 82(1) (2007), 61–77.Google Scholar
Baake, M. and Moody, R. V.. Weighted Dirac combs with pure point diffraction. J. Reine Angew. Math. 573 (2004), 61–94.Google Scholar
Baake, M., Moody, R. V. and Schlottmann, M.. Limit-(quasi) periodic point sets as quasicrystals with p-adic internal spaces. J. Phys. A: Math. Gen. 31(27) (1998), 5755.CrossRefGoogle Scholar
Barge, M. and Kellendonk, J.. Proximality and pure point spectrum for tiling dynamical systems. Michigan Math. J. 62(4) (2013), 793–822.Google Scholar
Berger, A., Siegmund, S. and Yi, Y.. On almost automorphic dynamics in symbolic lattices. Ergod. Th. & Dynam. Sys. 24 (2004), 677–696.Google Scholar
Bułatek, W. and Kwiatkowski, J.. Strictly ergodic Toeplitz flows with positive entropies and trivial centralizers. Studia Math. 103(2) (1992), 133–142.CrossRefGoogle Scholar
Downarowicz, T.. Survey on odometers and Toeplitz flows. Algebraic and Topological Dynamics (Contemporary Mathematics, 385) . Eds. Kolyada, S., Manin, Y. and Ward, T.. American Mathematical Society, Providence, RI, 2005, pp. 7–38.Google Scholar
Glasner, E.. On tame dynamical systems. Colloq. Math. 105 (2006), 283–295.Google Scholar
Glasner, E.. Enveloping semigroups in topological dynamics. Topology Appl. 154(11) (2007), 2344–2363.Google Scholar
Glasner, E.. The structure of tame dynamical systems. Ergod. Th. & Dynam. Sys. 27(6) (2007), 1819–1837.Google Scholar
Glasner, E. and Megrelishvili, M.. Hereditarily non-sensitive dynamical systems and linear representations. Colloq. Math. 104 (2006), 223–283.Google Scholar
Glasner, E., Megrelishvili, M. and Uspenskij, V.. On metrizable enveloping semigroups. Israel J. Math. 164 (2008), 317–332.CrossRefGoogle Scholar
Kellendonk, J. and Sadun, L.. Meyer sets, eigenvalues, and Cantor fiber bundles. J. Lond. Math. Soc. 89 (2014), 114–130.CrossRefGoogle Scholar
Lagarias, J.. Meyer’s concept of quasicrystals and quasiregular sets. Comm. Math. Phys. 179 (1996), 365–376.Google Scholar
Lee, J.-Y. and Moody, R. V.. A characterization of model multi-colour sets. Ann. Henri Poincaré 7(1) (2006), 125–143.Google Scholar
Markley, N. G. and Paul, M. E.. Almost automorphic symbolic minimal sets without unique ergodicity. Israel J. Math. 34(3) (1979), 259–272.Google Scholar
Moody, R. V.. Meyer sets and their duals. The Mathematics of Long-Range Aperiodic Order. Ed. Moody, R. V.. Kluwer, Dordrecht, 1997, pp. 403–442.Google Scholar
Moody, R. V.. Mathematical quasicrystals: a tale of two topologies. Proc. XIVth Int. Congress on Mathematical Physics (2003). Ed. Zambrini, J.-C.. World Scientific, Singapore, 2006.Google Scholar
Moody, R. V. and Strungaru, N.. Point sets and dynamical systems in the autocorrelation topology. Canad. Math. Bull. 47 (2004), 82–99.Google Scholar
Paul, M. E.. Construction of almost automorphic minimal flows. Appl. Gen. Topol. 6(1) (1976), 45–56.Google Scholar
Schlottmann, M.. Cut-and-project sets in locally compact Abelian groups. Quasicrystals and Discrete Geometry (Toronto, ON, 1995) (Fields Institute Monographs, 10) . American Mathematical Society, Providence, RI, 1998, pp. 247–264.Google Scholar
Veech, W. A.. Point distal flows. Amer. J. Math. 92(1) (1970), 205–242.CrossRefGoogle Scholar