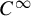On bifurcation of statistical properties of partially hyperbolic endomorphisms

Abstract

We give an example of a path-wise connected open set of $C^{\infty }$ partially hyperbolic endomorphisms on the $2$-torus, on which the (unique) Sinai–Ruelle–Bowen (SRB) measure exists for each system and varies smoothly depending on the system, while the sign of its central Lyapunov exponent changes.

1 Introduction

In this paper, we present an example of an open connected set of smooth maps on the $2$ -torus $\mathbb {T}^2$ for which the (unique) Sinai–Ruelle–Bowen (SRB) measure depends on the system smoothly while one of its Lyapunov exponents changes its sign. This implies that the statistical properties of smooth dynamical systems can be robust despite drastic changes of geometric structure.

Let us consider a dynamical system generated by a $C^\infty $ map $F:M\to M$ on a two-dimensional closed $C^\infty $ Riemann manifold M. We suppose that F is a local diffeomorphism and not injective. The Lyapunov exponent of F is defined by

$$ \begin{align*} \chi(v)=\limsup_{n\to \infty} \frac{1}{n} \log \lVert dF^n(v)\rVert \quad \text{for }v\in TM. \end{align*} $$

We write $\chi _1(x;F)\le \chi _2(x;F)$ for the values that $\chi (v)$ takes for $v\in T_xM\setminus \{0\}$ . These are important characteristics which describe the local geometric properties of the dynamics and play major roles in smooth ergodic theory (or Pesin theory). See [3, 13, 16] for instance.

To proceed, let us consider a one-parameter family $F_s:M\to M$ , $s\in [0,1]$ , of local diffeomorphisms as F above. Assume that, at the parameters $s=0$ and $s=1$ , the dynamical system $F_s$ admits an SRB measure, which is by definition an invariant probability measure $\mu _s$ such that

$$ \begin{align*} \frac{1}{n}\sum_{k=0}^{n-1}\delta_{F_s^k(x)} \to \mu_s \quad \text{weakly} \end{align*} $$

for almost every $x\in M$ with respect to the Riemann volume m on M. Assume also that, at the parameter $s=0$ and $s=1$ , the Lyapunov exponents $\chi _1(x;F_s)\le \chi _2(x;F_s)$ are constant and satisfy

$$ \begin{align*} \chi_1(x;F_0)<0< \chi_2(x;F_0) \quad\text{and}\quad 0<\chi_1(x;F_1)< \chi_2(x;F_1) \end{align*} $$

for almost every x with respect to m. These imply that the local geometric structure of the orbits of $F_0$ and $F_1$ are totally different. Indeed, most of points on M will have local stable manifold for $F_0$ but this will not be the case for $F_1$ . (See [3, 16].) It is then natural to expect drastic geometric (or topological) bifurcation phenomena of the dynamics of $F_s$ as the parameter s varies from $0$ to $1$ .

A general question we would like to pose is whether such geometric changes in the dynamics necessarily lead to some bifurcations of statistical properties of $F_s$ . Here, we present an open set of examples where we hardly observe such bifurcations. More precisely, we will show that there exists a path-wise connected open subset ${\mathcal {U}}$ in the space $C^\infty (\mathbb {T}^2)$ of $C^\infty $ mappings on the torus $\mathbb {T}^2$ such that the SRB measure $\mu _F$ depends on F smoothly and there exist $F_+$ and $F_-$ in ${\mathcal {U}}$ such that

$$ \begin{align*} \chi_1(x;F_-)<0<\chi_2(x;F_-), \quad 0<\chi_1(x;F_+)<\chi_2(x;F_+) \end{align*} $$

for almost every point $x\in M$ . Then any $C^\infty $ one-parameter family that connects $F_-$ and $F_+$ in ${\mathcal {U}}$ will be of the kind that we mentioned.

The idea behind the construction of the open subset ${\mathcal {U}}$ as above can be explained as follows. Let us consider a skew product map on the $2$ -torus

(1) $$ \begin{align} F:\mathbb{T}^2\to \mathbb{T}^2,\quad F(x,y)=(mx, g_x(y)). \end{align} $$

Its iteration is written

$$ \begin{align*} F^n(x)=(m^n x, g^{(n)}_x(y))\quad\text{where } g^{(n)}_x(y)= g_{m^{n-1}x}\circ \cdots \circ g_{mx}\circ g_x(y). \end{align*} $$

In the x-component, the dynamics is an angle-multiplying map and is strongly chaotic. In the y-component, the coordinate $g^{(n)}_x(y)$ is the composition of maps $g_z$ for the points z along the orbit of the dynamics in the x-component and hence we may regard it as a ‘random dynamical system’ driven by the strongly chaotic dynamics in the x-component. We refer to [2, 14] for the general theory of random dynamical systems.

For random dynamical systems, under some mild assumptions on the transition density, a unique invariant density exists and depends on the system smoothly. So bifurcations of the original (non-random) system do not necessarily lead to that of the randomized system. See [7, 8] for more detailed arguments relevant to the result of this paper. From the comparison mentioned in the last paragraph, it is then not surprising that the SBR measure of the map F in equation (1) can depend on F smoothly even at the parameter where the Lyapunov exponent of the SRB measure in the y-direction changes its sign.

To proceed along the idea explained above and to construct the open subset ${\mathcal {U}}\subset C^\infty (\mathbb {T}^2)$ , it is convenient to consider in the framework of a partially hyperbolic dynamical system. Partially hyperbolic dynamical systems have been studied extensively from many aspects since the works of Brin, Pesin, Grayson, Pugh, and Shub. (See [1, 4, 5, 10, 19].) For recent works relevant to the argument in this paper, we refer to [6, 11, 15, 17, 20] and the references therein. Note that there are a few slight variations in the definition of partial hyperbolicity. For definiteness, let us recall a definition of partially hyperbolic endomorphism in the two-dimensional non-invertible setting given in [17].

Definition. A $C^{\infty }$ map $F:M\to M$ on a surface M is said to be partially hyperbolic if there are positive constants $\unicode{x3bb} $ and c and a continuous decomposition of the tangent bundle $TM=E^c\oplus E^u$ with $\dim E^c=\dim E^u=1$ such that:

1. (a) $\lVert DF^n|_{E^u(z)}\rVert>\exp (\unicode{x3bb} n-c)$ ;

2. (b) $\lVert DF^n|_{E^c(z)}\rVert <\exp (-\unicode{x3bb} n+c)\lVert DF^n|_{E^u(z)}\rVert $

for all $z\in M$ and $n\ge 0$ .

Remark 1. In the definition above, the decomposition $TM=E^c\oplus E^u$ is not necessarily invariant nor smooth. However, the component $E^c$ turns out to be invariant as a consequence of the conditions (a) and (b).

The subset of partially hyperbolic endomorphisms is $C^1$ open in the space of $C^\infty $ self mappings on M. A primitive idea in the study of a partially hyperbolic dynamical system is that the dynamics in the direction of the unstable subbundle $E^u$ is uniformly expanding and, under some generic conditions, it induces some ‘randomness’ in the dynamics in the transversal direction in the manner explained above in the case of the skew product in equation (1). And, with this idea in mind, it is not surprising that the analogy of the skew product map in equation (1) with random dynamical systems extends, at least, to some open subset of partially hyperbolic dynamical systems.

Still, we would like to emphasize that not much is known about what can happen exactly at the parameter where the Lyapunov exponent of the SRB measure in the central direction $E^c$ changes its sign. As we wrote in the beginning, since a switch of the sign of the Lyapunov exponent implies drastic changes of the geometric structure of the dynamics, it is not easy to convince oneself that the statistical properties of smooth dynamical systems can be robust under such changes. And our example shows that there are such cases indeed. To illustrate what the dynamics and their bifurcations in our examples look like, we give a few results of numerical computations in §6.

2 Result

We write $\mathbb {T}={\mathbb {R}}/\mathbb {Z}$ for the unit circle and $\mathbb {T}^2$ for the two-dimensional torus. We consider the iteration of a $C^\infty $ local diffeomorphism $F:\mathbb {T}^2\to \mathbb {T}^2$ as a discrete dynamical system. The Perron–Frobenius operator

(2) $$ \begin{align} {\mathcal{P}}:C^r(\mathbb{T}^2)\to C^r(\mathbb{T}^2), \quad {\mathcal{P}} u(p)= \sum_{p'\in \mathbb{T}^2: F(p')=(p)}\frac{u(p')}{\lvert \det DF(p')\rvert} \end{align} $$

expresses the action of F on the space of densities, where $C^r(\mathbb {T}^2)$ denotes the space of $C^r$ functions on $\mathbb {T}^2$ .

An invariant Borel probability measure $\mu $ is said to be an SRB measure if almost every point on $\mathbb {T}^2$ with respect to the Lebesgue measure is generic for $\mu $ . We consider a partially hyperbolic endomorphism F on $\mathbb {T}^2$ and suppose that F admits an ergodic SRB measure $\mu _F$ . Then the Lyapunov exponents take constant values

$$ \begin{align*} \chi^c(\mu_F) < \chi^u(\mu_F)\quad\text{with } \chi^u(\mu_F)>0 \end{align*} $$

at almost every point with respect to $\mu _F$ and also with respect to the Lebesgue measure.

Our main result is stated as follows.

Theorem 1. For any $r>0$ , there exists a path-wise connected $C^\infty $ open subset $\mathcal {U}$ of $C^\infty (\mathbb {T}^2,\mathbb {T}^2)$ that consists of partially hyperbolic local diffeomorphisms, a Hilbert space

(3) $$ \begin{align} C^\infty(\mathbb{T}^2)\subset \mathcal{H}\subset C^r(\mathbb{T}^2), \end{align} $$

and a constant $0<\rho <1$ such that the following hold.

1. (a) The Perron–Frobenius operator $\mathcal {P}_F$ for $F\in \mathcal {U}$ restricts to a bounded operator

   (4) $$ \begin{align} {\mathcal{P}}_F:\mathcal{H}\to \mathcal{H}. \end{align} $$

2. (b) The restriction in equation (4) has a simple eigenvalue $1$ and the rest of its spectral set is contained in the disk $\lvert z\rvert < \rho < 1$ .

3. (c) $F\in \mathcal {U}$ admits a unique SRB measure $\mu _F=\rho _F \mathrm {Leb}$ where $\rho _F\in \mathcal {H}$ is the eigenfunction of ${\mathcal {P}}_F$ for the simple eigenvalue $1$ .

4. (d) The SRB measure $\mu _F$ depends on $F\in \mathcal {U}$ smoothly in the sense that, for any $C^\infty $ one-parameter family $G_t$ of maps in $\mathcal {U}$ and $\psi \in C^\infty (\mathbb {T}^2)$ , the correspondence $t\mapsto \int \psi \,d\mu _{G_t}$ is a $C^r$ function.

5. (e) There are $F_{\sigma }\in \mathcal {U}$ for $\sigma \in \{+,-\}$ such that the central Lyapunov exponent $\chi ^c(\mu _{F_\sigma })$ has the same sign as $\sigma $ .

The claims of the theorem above imply that, if we take any $C^\infty $ one-parameter family $G_t$ that connects $F_-$ and $F_+$ in $\mathcal {U}$ , we observe that the SRB measure $\mu _{G_t}$ varies smoothly with respect to t while the central Lyapunov exponent will change its sign at some parameter.

Remark 2. The conclusions of Theorem 1 imply more about the statistical properties of $F\in {\mathcal {U}}$ and their smooth dependence on F. For instance, the central limit theorem for smooth observables holds for $F\in {\mathcal {U}}$ and, for each fixed observable, the variance of the normal distribution in the limit depends on F smoothly. See [12].

3 Circle endomorphisms

We first consider the doubling map on the circle $\mathbb {T}$ :

$$ \begin{align*} f_0:\mathbb{T}\to \mathbb{T}, \quad f_0(y)=2y \ \mod\mathbb{Z}. \end{align*} $$

Below, we deform the map $f_0$ to make a neutral fixed point in a small neighborhood of $0\in \mathbb {T}$ .

Let $\varphi :{\mathbb {R}}\to {\mathbb {R}}$ be a $C^\infty $ map with the following properties:

1. (i) $0\le \varphi (y)\le 1$ and $\lvert \varphi '(y)\rvert \le 4/3$ for $y\in {\mathbb {R}}$ ;

2. (ii) $\varphi (y)=0$ for $y\notin [1/10,1]$ ;

3. (iii) $\varphi (1/2)=1/2$ , $\varphi '(1/2)=1$ , $\varphi "(1/2)<0$ ; and

4. (iv) $\varphi (y)<y$ for $y\in (0,1)\setminus \{1/2\}$ .

For a small real number $\varepsilon>0$ , we define

$$ \begin{align*} f_{\varepsilon}:\mathbb{T}\to \mathbb{T}, \quad f_\varepsilon(y)= \begin{cases} f_0(y)-\varepsilon \cdot \varphi(\varepsilon^{-1}y)&\quad \text{if } y\in [0,\varepsilon];\\ f_0(y)&\quad\text{otherwise.} \end{cases} \end{align*} $$

For the dynamics of $f_\varepsilon $ , we observe that there are only two fixed points $0$ and $P=\varepsilon /2$ : $0$ is a hyperbolic repelling fixed point and $P=\varepsilon /2$ is a one-sided attracting neutral fixed point with immediate basin $(0,P]$ . See Figure 1 for the graph of $f_\varepsilon $ .

Figure 1 The graph of the function $f_\varepsilon $ .

We henceforth suppose that the parameter $\varepsilon>0$ is sufficiently small, say $0<\varepsilon <1/100$ . Then, for $a\in {\mathbb {R}}$ , we set

(5) $$ \begin{align} f_{\varepsilon,a}:\mathbb{T}\to \mathbb{T}, \quad f_{\varepsilon,a}(y)=f_{\varepsilon}(y)+a\varepsilon. \end{align} $$

From assumption (iv) on $\varphi $ , we have

$$ \begin{align*} \frac{2}{3}\le f'_{\varepsilon,a}(y)\le \frac{10}{3}\quad \text{for any }y\in \mathbb{T}. \end{align*} $$

Hence, if $a\ge 1$ , we have that $f_{\varepsilon ,a}^{-1}([0,\varepsilon ])\cap (0,\varepsilon )=\emptyset $ and hence

(6) $$ \begin{align} (f_{\varepsilon,a}^2)'(y)\ge 2\cdot \frac{2}{3}=\frac{4}{3}>1\quad \text{for any }y\in \mathbb{T}. \end{align} $$

The family $a\mapsto f_{\varepsilon ,a}$ exhibits the saddle-node bifurcation of the fixed point $0$ at the parameter $a=0$ . It is not difficult to check that $f_{\varepsilon ,a}$ is uniformly expanding if $0<a\le 2$ . If $a<0$ and $\lvert a\rvert $ is sufficiently small, then $f_{\varepsilon ,a}$ admits three fixed points

$$ \begin{align*} 0<P_0=-a\varepsilon <P_-<P_+ \end{align*} $$

in a small neighborhood of $0$ , where $P_0$ and $P_+$ are hyperbolic repelling while $P_-$ is hyperbolic attracting. The immediate basin of the hyperbolic attracting fixed point $P_-$ is the interval $B=(P_0,P_+)$ and we have

$$ \begin{align*} \lim_{a\to -0} P_0=0,\quad \lim_{a\to -0} P_-=\lim_{a\to -0} P_+=\frac{\varepsilon}{2}. \end{align*} $$

4 Skew products over angle-multiplying maps

We consider the dynamics of perturbations of the skew product

$$ \begin{align*} F_{\varepsilon,a,\delta,m}:\mathbb{T}^2\to \mathbb{T}^2,\quad F_{\varepsilon,a,\delta,m}(x,y)=(mx, f_{\varepsilon,a}(y)+ \delta \varepsilon \cos 2\pi x), \end{align*} $$

where m is a positive integer and $\delta>0$ is a positive real parameter. In the following, we suppose that $r>0$ is a given integer. We suppose that the constants $\varepsilon>0$ and $\delta>0$ are small, say $\varepsilon ,\delta \in (0,1/100)$ . We will also fix m as a large constant so that the conclusion of Theorem 2 below holds true. Since we regard $F_{\varepsilon ,a,\delta ,m}$ as a one-parameter family with parameter $a\in [-2\delta ,2]$ , we henceforth write $F_a$ for $F_{\varepsilon ,a,\delta ,m}$ .

4.1 Quasi-compactness of $\mathcal {P}$

We adapt the argument in [20] to get the next theorem. Since the situation is only a little different from that in [20], we give a brief account on its proof in §5.

Theorem 2. Let $0<\rho _0<1$ be a given real number. If we let m be sufficiently large depending on the parameters r, $\varepsilon $ , $\delta $ , and $\rho _0$ , the following hold true.

There exist a $C^\infty $ neighborhood $\mathcal {U}\subset C^\infty (\mathbb {T}^2,\mathbb {T}^2)$ of the family $\mathcal {F}=\{F_a=F_{\varepsilon ,a,\delta ,m}, a\in [-2\delta ,2]\}$ and a Hilbert space $\mathcal {H}$ satisfying equation (3) such that, for any $F\in \mathcal {U}$ , the Perron–Frobenius operator ${\mathcal {P}}_F:\mathcal {H}\to \mathcal {H}$ is bounded and its essential spectral radius is bounded by $\rho _0$ , which is strictly smaller than its spectral radius $1$ .

Further, if $1$ is a simple eigenvalue of ${\mathcal {P}}_F:\mathcal {H}\to \mathcal {H}$ for every $F\in \mathcal {F}$ , then, by letting the neighborhood $\mathcal {U}$ be smaller, we may suppose that the same is true for all $F\in \mathcal {U}$ and the positive eigenfunction $\rho _F\in \mathcal {H}$ for the simple eigenvalue $1$ , normalized by the condition $\int \rho _F \,d\mathrm {Leb} =1$ , depends on F smoothly in the following sense: for any $C^\infty $ one-parameter family $G_t$ of maps in $\mathcal {U}$ and $\psi \in C^\infty (\mathbb {T}^2)$ , the correspondence $t\mapsto \int \psi \,d\mu _{G_t}=\int \psi \rho _{G_t}\, d\mathrm {Leb}$ is a $C^r$ function.

Remark 3. We cannot let $r=\infty $ in our construction because it is essential to take m large enough depending on r.

4.2 Simplicity of the eigenvalue $1$

We show the following theorem for the family $\mathcal {F}=\{F_a=F_{\varepsilon ,a,\delta ,m}\mid a\in [-2\delta ,2]\}$ .

Theorem 3. For any $a\in [-2\delta ,2]$ , the principal eigenvalue $1$ of ${\mathcal {P}}_F:\mathcal {H}\to \mathcal {H}$ is simple and there is no other eigenvalue on the unit circle. The eigenfunction $\rho _a\in \mathcal {H}$ for the simple eigenvalue $1$ satisfying $\int \rho _a\, d\mathrm {Leb}=1$ is the density of the SRB measure $\mu _{a}$ with respect to the Riemann volume m on $\mathbb {T}^2$ .

Proof. We consider the following two cases for $a\in [-2\delta ,2]$ separately:

$$ \begin{align*} \textrm{(i)}\; a+\delta>0;\quad \textrm{(ii)}\; a+\delta\le 0. \end{align*} $$

Case (i). First we prove the following lemma.

Lemma 4. In Case (i), we have $U_\infty :=\bigcup _{n\ge 0}F_a^n(U)=\mathbb {T}^2$ for any non-empty open subset U on $\mathbb {T}^2$ .

Proof. Since $F_a$ is expanding in the horizontal (or x-) direction, we have that $U_\infty \cap (\{0\}\times \mathbb {T})\neq \emptyset $ . The map $F_{a}$ restricted to $\{0\}\times \mathbb {T}$ can be identified with $f_{\varepsilon ,a+\delta }$ . From the assumption, we have $a+\delta>0$ and hence $f_{\varepsilon ,a+\delta }$ is uniformly expanding, provided that $\delta>0$ is sufficiently small.

Remark 4. The last claim is not completely obvious but easy to check. Let $f=f_{\varepsilon ,a}$ . To show that f is uniformly expanding, it is enough to show that there exists $n>0$ for any $x\in \mathbb {T}$ such that $(f^n)'(x)>1$ . This holds obviously with $n=1$ for x on the outside of $(0,\varepsilon )$ . For a point $x\in (0,\varepsilon )$ , we let k be the smallest integer such that $f^{k}(x)\notin (0,\varepsilon )$ . By the elementary estimates on an intermittent one-dimensional map, we see that $(f^{k})'(x)>h>0$ for some constant $h>0$ independent of $a>0$ and $\varepsilon>0$ (as far as they are sufficiently small). By letting $\varepsilon>0$ be sufficiently small, we may suppose that the orbit starting from $f^{k}(x)$ will not return to $(0,\varepsilon )$ for arbitrarily long time and therefore we can find $n>k$ such that $(f^{n})'(x)>1$ .

Hence, we have $U_\infty \supset \{0\}\times \mathbb {T}$ . Again, using the fact that $F_a$ is expanding in the horizontal direction, we obtain the claim $U_\infty =\mathbb {T}^2$ .

Suppose that $\rho \in \mathcal {H}$ is an eigenfunction for an eigenvalue on the unit circle. Then we have $\lvert \mathcal {P}^n\rho \rvert = \lvert \rho \rvert =\mathcal {P}^n\lvert \rho \rvert $ for $n\ge 1$ . From the last lemma, this holds only if $\rho =e^{i\theta } \lvert \rho \rvert $ for some $\theta \in [0,2\pi )$ and therefore we may suppose $\rho \ge 0$ . This implies that there is no eigenvalue on the unit circle other than $1$ . For the same reason, the geometric multiplicity of the eigenvalue $1$ should be $1$ . Further, since $\mathcal {P}$ preserves the integral of functions with respect to the Lebesgue measure, we conclude that the algebraic multiplicity is not greater than $1$ .

Let $\rho _{F_a}\in \mathcal {H}\subset C^r(\mathbb {T}^2)$ be the eigenfunction of ${\mathcal {P}}_{F_a}$ for the simple eigenvalue $1$ . We may and do suppose that $\rho _{F_a}$ is non-negative and $\int \rho _{F_a} \,d\mathrm {Leb}=1$ . Then the measure $\nu _{F_a}:=\rho _{F_a} \,\mathrm {Leb}$ is ergodic since $\mathcal {P}^n u$ converges to a constant multiple of $\rho _{F_a}$ for any $u\in \mathcal {H}$ . Since $\rho _{F_a}\in C^r(\mathbb {T})$ , there is an open subset $U\subset \mathbb {T}^2$ on which $\rho _{F_a}>0$ and therefore almost every point in U is generic for $\mu _{F_a}$ . As $F_a$ is a local diffeomorphism, almost every point on $F_a^n(U)$ with $n\ge 0$ is generic for $\mu _{F_a}$ . Since $\bigcup _{n\ge 0}F_a^n(U)=\mathbb {T}^2$ , as we showed in Lemma 4, we conclude that almost every point on $\mathbb {T}^2$ is generic for $\mu _{F_a}$ . This finishes the proof of the theorem in Case (i).

Case (ii). Note that $a\le -\delta <0$ in this case. The region

$$ \begin{align*} W=\mathbb{T}\times ((\delta-a)\varepsilon, \varepsilon/2) \end{align*} $$

satisfies $F_a(W)\subset W$ and the iteration of $F_a$ is (non-uniformly) contracting on the fibers $\{x\}\times ((\delta -a)\varepsilon , \varepsilon /2)$ for $x\in \mathbb {T}$ .

Remark 5. The choice of the interval $(\delta -a)\varepsilon ,\varepsilon /2)$ in the definition of W is made as follows. The left end point $y_-=(\delta -a)\varepsilon $ is the unique point in $(0,\varepsilon /10)$ satisfying $ f_{\varepsilon ,a-\delta }(y_-)=y_-$ . (Recall condition (ii) in the definition of the function $\varphi $ .) The right end point $y_+=\varepsilon /2$ is the neutral fixed point of $f_{\varepsilon ,0}$ , which satisfies $f_{\varepsilon ,a+\delta }(y_+)\le y_+$ when $a+\delta \le 0$ .

Hence, there exists a unique mixing $F_a$ -invariant measure $\mu _{F_a}$ supported in W such that Lebesgue almost every point on W is generic for $\mu _{F_a}$ .

Writing $\pi _2:{\mathbb {R}}^2\to {\mathbb {R}}$ for the projection to the second component, we have $\pi _2\partial _y (F_{a}\circ F_{a})(p)>1$ on the complement of $F_a^{-1}(W)$ , with only one exception $p=(0,\varepsilon /2)$ when $a+\delta =0$ . Hence, the intersection of the complement

$$ \begin{align*} C=\mathbb{T}^2\setminus \bigcup_{n\ge 0} F_{a}^{-n}(W) \end{align*} $$

with any fiber $\{x\}\times \mathbb {T}$ cannot contain any non-trivial interval.

We next show that the complement C is of null Lebesgue measure. Suppose that C has positive Lebesgue measure and write $\mathbf {1}_{C}$ for the characteristic function of it. Then we can find a weak limit point $\rho $ of the sequence $(1/n)\sum _{k=0}^{n-1}\mathcal {P}^k\mathbf {1}_{C}$ . By approximating $\mathbf {1}_{C}$ by the $C^\infty $ function in an $L^1$ sense and using the spectral property of ${\mathcal {P}}$ in Theorem 2, we see that $\rho $ belongs to $\mathcal {H}\subset C^r(\mathbb {T}^2)$ and is supported on C. However, this is impossible because C has no interior point.

Since the complement C is of null Lebesgue measure, almost every point on $\mathbb {T}^2$ is generic for the mixing measure $\mu _F$ . This implies the conclusion of the theorem.□

Finally, we prove the following theorem on the central Lyapunov exponent of the SRB measure $\mu _{F_a}$ for $F_a$ with $a\in [-2\delta ,2]$ . Note that we always assume that $\varepsilon>0$ and $\delta>0$ are small.

Theorem 5

1. (a) If $a+\delta <0$ , the central Lyapunov exponent $\chi ^c(\mu _{F_a})$ is negative.

2. (b) If $a\ge 1$ , the central Lyapunov exponent $\chi ^c(\mu _{F_a})$ is positive.

Proof. (a) As we observed in the proof of Theorem 3 in Case (ii), there is a unique SRB measure $\mu _{F_a}$ whose support is contained in W and its central Lyapunov exponent is negative.

(b) By equation (6), the map $F_{a}$ is expanding along the fibers in this case and therefore the central Lyapunov exponent of the SRB measure is positive, provided that $\delta>0$ is sufficiently small.

We can now deduce Theorem 1 from Theorems 2, 3, and 5.

5 The proof of Theorem 2

We can obtain the proof of Theorem 2 by following the argument in [20] with slight modifications. Below, we explain briefly how we modify the argument in [20].

First, we check a kind of transversality condition. We consider the constant cones in the tangent bundle

$$ \begin{align*} \mathbf{C}=\bigcup_{p\in \mathbb{T}^2} \mathbf{C}_p =\{(p,v)=((x,y),(v_x,v_y))\in T\mathbb{T}^2\mid \lvert v_y\rvert\le C_0\delta\varepsilon \lvert v_x\rvert\}, \end{align*} $$

where we fix a large constant $C_0$ so that $DF(\mathbf {C})\subset \mathbf {C}$ . For given $p\in \mathbb {T}^2$ and $q,q'\in \mathbb {T}^2$ , we write $q\pitchfork q'$ if

$$ \begin{align*} DF_q(\mathbf{C})\cap DF_{q'}(\mathbf{C})=\{0\}. \end{align*} $$

We define

$$ \begin{align*} \mathbf{m}(F)=\frac{1}{(2/3)\cdot m}\cdot \sup_{p\in \mathbb{T}^2}\sup_{q\in F^{-1}(p)} \#\{q'\in F^{-1}(p)\mid q'\pitchfork q\}, \end{align*} $$

where $(2/3)\cdot m$ stands for a lower bound of $\det dF$ . We can check the following lemma by crude estimates. (We can actually prove $\mathbf {m}(F)<const.\; m^{-1/2}$ . One can find a relevant computation in [18, Appendix].)

Lemma 6. The quantity $\mathbf {m}(F)$ converges to $0$ when we let m go to infinity and the convergence is uniform for sufficiently small $\varepsilon>0$ , $\delta>0$ , and any $a\in [-2,2]$ .

We then follow the argument in [20] almost literally, noting that $\mathbf {m}(F)$ corresponds to $m(f,1)$ defined in [20, §3] and that we just consider the first iteration (or the case $n=1$ there). Note also that we consider nonlinear endomorphisms in equation (5) on the fibers though the corresponding maps are rigid rotations in [20]. However, since we just consider the first iteration, if we take sufficiently fine local charts and a $C^\infty $ partition of unity subordinate to them in the argument in [20, §4], it is direct to get a parallel argument in our setting. Then the claim corresponding to [20, Proposition 3] and Hennion’s theorem give the former part of Theorem 2 on the essential spectral radius of $\mathcal {P}_F$ . We can deduce the latter part using the abstract perturbation theorem in [9, §8] about perturbation of transfer operators. For this, we again follow the argument in [20, §4.4].

6 Some numerical experiments

We present some results of numerical experiments related to the claim of the main theorem. For simplicity of computation, we consider a similar but slightly different setting from that in the previous sections. We consider a $C^\infty $ map $f:\mathbb {T}\to \mathbb {T}$ defined by

$$ \begin{align*} f(y)=2y - \frac{\sin(2\pi y)+\cos(2\pi x)-1}{2\pi} \ \mod \mathbb{Z}. \end{align*} $$

It has a neutral fixed point at $0$ and its dynamics is very similar to that of $f_\varepsilon $ in §3. (The graph of the function f is depicted in Figure 2.)

Figure 2 The graph of the function f.

Then we consider a family of dynamical systems $F_a:\mathbb {T}^2\to \mathbb {T}^2$ defined by

$$ \begin{align*} F_a(x,y)= (7x, f(y)+\delta \cdot \cos(2\pi x)+a)\quad \text{for } a\in [-2\delta,2\delta], \end{align*} $$

where we set $\delta =10^{-2}$ . In Figure 3, we compute the approximate central Lyapunov exponent at a randomly chosen point by iterating F for $10^6$ times and plot it against the parameters $-0.02\le a\le 0.02$ (respectively $-0.004\le a\le 0.004$ ) with step $10^{-3}$ (respectively $10^{-4}$ ). We observe that the (central) Lyapunov exponent varies smoothly and changes its sign at a parameter $-0.001<a_0<0$ .

Figure 3 The central Lyapunov exponent of the SRB measure as a function of the parameters a close to $0$ . We draw the graph with the domain $[-0.02,0.02]$ and $[-0.004,0.004]$ respectively on the left and right pictures.

We also plot an orbit of randomly chosen initial point at the parameters $a=-0.02, -0.006,-0.003, -0.002$ . (We draw the orbit from time $10^3$ to time $10^6$ .) At the parameter $a=-0.02$ , we observe that the orbits are trapped by a horizontal zonal region. When the parameter a crosses the value $-\delta =-0.01$ , we expect that the orbits start to spread over the whole space $\mathbb {T}^2$ and, as the parameter a gets large, the density of the orbits becomes more uniform. However, when the value of a is close to $-0.01$ , it is difficult to detect this phenomenon because only a very small portion of orbits go out of (the ruin of) the attracting region and return to it again soon. (See the picture for the parameter $a=-0.006$ in Figure 4.)

Figure 4 Plots of orbits of $F_a$ at a few values of the parameter a.