Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T05:01:55.297Z Has data issue: false hasContentIssue false
  • English
  • Français

On an extension of Mycielski’s theorem and invariant scrambled sets

Published online by Cambridge University Press:  10 November 2014

FENG TAN
FENG TAN*
Affiliation:
School of the Mathematical Science, South China Normal University, Guangzhou Guangdong 510631, PR China email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $(X,f)$ be a dynamical system, where 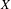$X$ is a perfect Polish space and 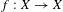$f:X\rightarrow X$ is a continuous map. In this paper we study the invariant dependent sets of a given relation string 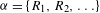${\it\alpha}=\{R_{1},R_{2},\ldots \}$ on 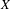$X$. To do so, we need the relation string ${\it\alpha}$ to satisfy some dynamical properties, and we say that ${\it\alpha}$ is 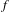$f$-invariant (see Definition 3.1). We show that if 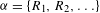${\it\alpha}=\{R_{1},R_{2},\ldots \}$ is an $f$-invariant relation string and 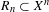$R_{n}\subset X^{n}$ is a residual subset for each 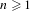$n\geq 1$, then there exists a dense Mycielski subset 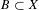$B\subset X$ such that the invariant subset 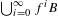$\bigcup _{i=0}^{\infty }f^{i}B$ is a dependent set of 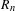$R_{n}$ for each 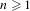$n\geq 1$ (see Theorems 5.4 and 5.5). This result extends Mycielski’s theorem (see Theorem A) when 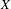$X$ is a perfect Polish space (see Corollary 5.6). Furthermore, in two applications of the main results, we simplify the proofs of known results on chaotic sets in an elegant way.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 2 , April 2016 , pp. 632 - 648
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akin, E.. Lectures on Cantor and Mycielski sets for dynamical systems. Chapel Hill Ergodic Theory Workshops (Contemporary Mathematics, 356). American Mathematical Society, Providence, RI, 2004, pp. 21–79.CrossRefGoogle Scholar
Akin, E., Glasner, E., Huang, W., Shao, S. and Ye, X.. Sufficient conditions under which a transitive system is chaotic. Ergod. Th. & Dynam. Sys. 30 (2010), 1277–1310.CrossRefGoogle Scholar
Balibrea, F., Smítal, J. and Stefankova, M.. The three versions of distribution chaos. Chaos Solitons Fractals 23 (2005), 1581–1583.Google Scholar
Blanchard, F., Glasner, E., Kolyada, S. and Maass, A.. On Li-Yorke pairs. J. Reine Angew. Math. 547 (2002), 51–68.Google Scholar
Blanchard, F., Huang, W. and Snoha, L.. Topological size of scrambled sets. Colloq. Math. 110 (2008), 293–361.CrossRefGoogle Scholar
Bowen, R.. Topological entropy and axiom A. Global Analysis (Proceedings of Symposia in Pure Mathematics, 14). American Mathematical Society, Providence, RI, 1970, pp. 23–41.CrossRefGoogle Scholar
Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527). Springer, Berlin, 1976.CrossRefGoogle Scholar
Foryś, M., Opricha, P. and Wilczyński, P.. Factor maps and invariant distributional chaos. J. Differential Equations 256 (2014), 475–502.CrossRefGoogle Scholar
Huang, W. and Ye, X.. Devaney’s chaos or 2-scattering implies Li-Yorke’s chaos. Topology Appl. 117 (2002), 259–272.CrossRefGoogle Scholar
Illanes, A. and Nadler, S. B. Jr. Hyperspaces: Fundamentals and Recent Advances (Monographs and Textbooks in Pure and Applied Mathematics, 216). Marcel Dekker, New York, 1999.Google Scholar
Iwanik, A.. Independence and scrambled sets for chaotic mappings. The Mathematical Heritage of C. F. Gauss. World Scientific, River Edge, NJ, 1991, pp. 372–378.CrossRefGoogle Scholar
Kato, H.. On scrambled sets and a theorem of Kuratowski on independent sets. Proc. Amer. Math. Soc. 126 (1998), 2151–2157.CrossRefGoogle Scholar
Kechris, A. S.. Classical Descriptive Set Theory. Springer, New York, 1995.CrossRefGoogle Scholar
Kuratowski, K.. Applications of the Baire-category method to the problem of independent sets, Collection of articles dedicated to Andrzej Mostowski on the occasion of his sixtieth birthday. Fund. Math. 81 (1973), 65–72.CrossRefGoogle Scholar
Mycielski, J.. Independent sets in topological algebras. Fund. Math. 55 (1964), 139–147.CrossRefGoogle Scholar
Oprocha, P.. Coherent lists and chaotic sets. Discrete Contin. Dyn. Syst. 31(3) (2011), 797–825.CrossRefGoogle Scholar
Schweizer, B. and Smítal, J.. Measures of chaos and a spectral decomposition of dynamical systems on the interval. Trans. Amer. Math. Soc. 344 (1994), 737–754.CrossRefGoogle Scholar
Xiong, J.. Chaos in a topologically transitive system. Sci. China 48(7) (2005), 929–939.CrossRefGoogle Scholar
Xiong, J., Tan, F. and Lü, J.. Dependent sets of a family of relations with full measure on a probability space. Sci. China 37(2) (2007), 220–228.Google Scholar
Yuan, D. and Lü, J.. Invariant scrambled sets in transitive systems. Adv. Math. 38(3) (2009), 302–308.Google Scholar