Hostname: page-component-745bb68f8f-f46jp Total loading time: 0 Render date: 2025-01-14T12:38:11.436Z Has data issue: false hasContentIssue false
  • English
  • Français

Odd and even Maass cusp forms for Hecke triangle groups, and the billiard flow

Published online by Cambridge University Press:  04 August 2014

ANKE D. POHL
ANKE D. POHL*
Affiliation:
Mathematisches Institut, Georg-August-Universität Göttingen, Bunsenstraße 3–5, 37073 Göttingen, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

By a transfer operator approach to Maass cusp forms and the Selberg zeta function for cofinite Hecke triangle groups, Möller and the present author found a factorization of the Selberg zeta function into a product of Fredholm determinants of transfer-operator-like families: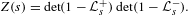

$$\begin{eqnarray}Z(s)=\det (1-{\mathcal{L}}_{s}^{+})\det (1-{\mathcal{L}}_{s}^{-}).\end{eqnarray}$$
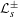In this article we show that the operator families ${\mathcal{L}}_{s}^{\pm }$ arise as families of transfer operators for the triangle groups underlying the Hecke triangle groups, and that for 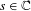$s\in \mathbb{C}$, 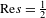$\text{Re}s={\textstyle \frac{1}{2}}$, the operator 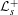${\mathcal{L}}_{s}^{+}$ (respectively 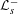${\mathcal{L}}_{s}^{-}$) has a 1-eigenfunction if and only if there exists an even (respectively odd) Maass cusp form with eigenvalue 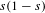$s(1-s)$. For non-arithmetic Hecke triangle groups, this result provides a new formulation of the Phillips–Sarnak conjecture on non-existence of even Maass cusp forms.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 36 , Issue 1 , February 2016 , pp. 142 - 172
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bruggeman, R., Lewis, J. and Zagier, D.. Period functions for Maass forms and cohomology. Memoirs of the AMS (2013), to appear.Google Scholar
Chang, C.-H. and Mayer, D.. The Transfer Operator Approach to Selberg’s Zeta Function and Modular and Maass Wave Forms for PSL(2, Z) (IMA Volumes in Mathematics and its Applications, 109). Springer, Berlin, 1999, pp. 73–141.Google Scholar
Chang, C.-H. and Mayer, D.. Eigenfunctions of the Transfer Operators and the Period Functions for Modular Groups (Contemporary Mathematics, 290). American Mathematical Society, Providence, RI, 2001, pp. 1–40.Google Scholar
Chang, C.-H. and Mayer, D.. An extension of the thermodynamic formalism approach to Selberg’s zeta function for general modular groups. Ergodic Theory, Analysis, and Efficient Simulation of Dynamical Systems. Springer, Berlin, 2001, pp. 523–562.CrossRefGoogle Scholar
Deitmar, A. and Hilgert, J.. A Lewis correspondence for submodular groups. Forum Math. 19(6) (2007), 1075–1099.CrossRefGoogle Scholar
Efrat, I.. Dynamics of the continued fraction map and the spectral theory of SL(2, Z). Invent. Math. 114(1) (1993), 207–218.CrossRefGoogle Scholar
Hejhal, D.. The Selberg Trace Formula for PSL(2, R), Vol. 2 (Lecture Notes in Mathematics, 1001). Springer, Berlin, 1983.CrossRefGoogle Scholar
Hilgert, J. and Pohl, A.. Symbolic dynamics for the geodesic flow on locally symmetric orbifolds of rank one. Proceedings of the Fourth German–Japanese Symposium on Infinite Dimensional Harmonic Analysis IV. On The Interplay Between Representation Theory, Random Matrices, Special Functions, and Probability. World Scientific, Singapore, 2009, pp. 97–111.Google Scholar
Judge, C.. On the existence of Maass cusp forms on hyperbolic surfaces with cone points. J. Amer. Math. Soc. 8(3) (1995), 715–759.CrossRefGoogle Scholar
Lewis, J.. Spaces of holomorphic functions equivalent to the even Maass cusp forms. Invent. Math. 127 (1997), 271–306.CrossRefGoogle Scholar
Lewis, J. and Zagier, D.. Period functions for Maass wave forms. I. Ann. of Math. (2) 153(1) (2001), 191–258.CrossRefGoogle Scholar
Mayer, D. H.. On the thermodynamic formalism for the Gauss map. Comm. Math. Phys. 130(2) (1990), 311–333.CrossRefGoogle Scholar
Mayer, D.. The thermodynamic formalism approach to Selberg’s zeta function for PSL(2, Z). Bull. Amer. Math. Soc. (N.S.) 25(1) (1991), 55–60.CrossRefGoogle Scholar
Mayer, D., Mühlenbruch, T. and Strömberg, F.. The transfer operator for the Hecke triangle groups. Discrete Contin. Dyn. Syst. Ser. A 32(7) (2012), 2453–2484.CrossRefGoogle Scholar
Morita, T.. Markov systems and transfer operators associated with cofinite Fuchsian groups. Ergod. Th. & Dynam. Sys. 17(5) (1997), 1147–1181.CrossRefGoogle Scholar
Möller, M. and Pohl, A.. Period functions for Hecke triangle groups, and the Selberg zeta function as a Fredholm determinant. Ergod. Th. & Dynam. Sys. 33(1) (2013), 247–283.CrossRefGoogle Scholar
Pohl, A.. Symbolic dynamics for the geodesic flow on locally symmetric good orbifolds of rank one, Dissertation Thesis, University of Paderborn, 2009, http://d-nb.info/gnd/137984863.Google Scholar
Pohl, A.. A dynamical approach to Maass cusp forms. J. Mod. Dyn. 6(4) (2012), 563–596.CrossRefGoogle Scholar
Pohl, A.. Period functions for Maass cusp forms for Γ0(p): A transfer operator approach. Int. Math. Res. Not. 14 (2013), 3250–3273.CrossRefGoogle Scholar
Pohl, A.. Symbolic dynamics for the geodesic flow on two-dimensional hyperbolic good orbifolds. Discrete Contin. Dyn. Syst. Ser. A 34(5) (2014), 2173–2241.CrossRefGoogle Scholar
Pohl, A.. A thermodynamic formalism approach to the Selberg zeta function for Hecke triangle surfaces of infinite area, Preprint, 2014, arXiv:1404.3934.CrossRefGoogle Scholar
Pollicott, M.. Some applications of thermodynamic formalism to manifolds with constant negative curvature. Adv. Math. 85 (1991), 161–192.CrossRefGoogle Scholar
Phillips, R. S. and Sarnak, P.. On cusp forms for co-finite subgroups of PSL (2, R). Invent. Math. 80(2) (1985), 339–364.CrossRefGoogle Scholar
Phillips, R. S. and Sarnak, P.. The Weyl theorem and the deformation of discrete groups. Comm. Pure Appl. Math. 38(6) (1985), 853–866.CrossRefGoogle Scholar
Rölcke, W.. Über die Wellengleichung bei Grenzkreisgruppen erster Art. Sitzungsber. Heidelberger Akad. Wiss., Math.-Naturw. Kl. 1953/1955(4) (1956).Google Scholar
Ruelle, D.. Zeta-functions for expanding maps and Anosov flows. Invent. Math. 34(3) (1976), 231–242.CrossRefGoogle Scholar
Selberg, A.. Göttingen lectures, unpublished.Google Scholar
Venkov, A.. Spectral theory of automorphic functions. Proc. Steklov Inst. Math. 4(153) (1982), A translation of Tr. Mat. Inst. Steklova 1 53 (1981).Google Scholar