Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T04:02:08.406Z Has data issue: false hasContentIssue false
  • English
  • Français

The nub of an automorphism of a totally disconnected, locally compact group

Published online by Cambridge University Press:  23 January 2013

GEORGE A. WILLIS
GEORGE A. WILLIS*
Affiliation:
Mathematical and Physical Sciences, University of Newcastle, Callaghan, NSW 2308, Australia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

To any automorphism, $\alpha $, of a totally disconnected, locally compact group, 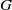$G$, there is associated a compact, $\alpha $-stable subgroup of 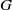$G$, here called the nub of $\alpha $, on which the action of $\alpha $ is ergodic. Ergodic actions of automorphisms of compact groups have been studied extensively in topological dynamics and results obtained transfer, via the nub, to the study of automorphisms of general locally compact groups. A new proof that the contraction group of $\alpha $ is dense in the nub is given, but it is seen that the two-sided contraction group need not be dense. It is also shown that each pair 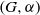$(G, \alpha )$, with 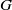$G$ compact and $\alpha $ ergodic, is an inverse limit of pairs that have ‘finite depth’ and that analogues of the Schreier refinement and Jordan–Hölder theorems hold for pairs with finite depth.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 4 , August 2014 , pp. 1365 - 1394
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aoki, N.. Dense orbits of automorphisms and compactness of groups. Topology Appl. 20 (1985), 1–15.Google Scholar
Baumgartner, U. and Willis, G. A.. Contraction groups and scales of automorphisms of totally disconnected locally compact groups. Israel J. Math. 142 (2004), 221–248.Google Scholar
Caprace, P.-E. and de Medts, T.. Simple locally compact groups acting on trees and their germs of automorphisms. Transform. Groups 16 (2) (2011), 375–411.Google Scholar
Dani, S. G., Shah, N. and Willis, G. A.. Locally compact groups with dense orbits under ${ \mathbb{Z} }^{d} $-actions by automorphisms. Ergod. Th. & Dynam. Sys. 26 (2006), 1443–1465.Google Scholar
van Dantzig, D.. Studien over topologische algebra. Dissertation, Amsterdam, 1931.Google Scholar
Fagnani, F.. Some results on the classification of expansive automorphisms of compact abelian groups. Ergod. Th. & Dynam. Sys. 16 (1996), 45–50.Google Scholar
Glöckner, H.. Contraction groups for tidy automorphisms of totally disconnected groups. Glasgow Math. J. 47 (2005), 329–333.Google Scholar
Glöckner, H. and Willis, G. A.. Classification of the simple factors appearing in composition series of totally disconnected contraction groups. J. Reine Angew. Math. 643 (2010), 141–169.Google Scholar
Haglund, F. and Paulin, F.. Simplicité de Groupes D’automorphismes D’espaces à Courbure Négative (Geometry & Topology Monographs, 1). Geometry and Topology Publishing, Coventry, 1998, pp. 181–48; The Epstein birthday schrift (electronic).Google Scholar
Halmos, P. R.. Lectures on Ergodic Theory. The Mathematical Society of Japan, Tokyo, 1956.Google Scholar
Hazod, W. and Siebert, E.. Automorphisms on a Lie group contracting modulo a compact subgroup and applications to semistable convolution semigroups. J. Theoret. Probab. 1 (1988), 211–225.Google Scholar
Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis I (Grundlehren der Mathematischen Wissenschaften, 115). Springer, Berlin, 1963.Google Scholar
Jaworski, W.. On contraction groups of automorphisms of totally disconnected locally compact groups. Israel J. Math. 172 (2009), 1–8.CrossRefGoogle Scholar
Jaworski, W.. Contraction groups, ergodicity, and distal properties of automorphisms of compact groups. Illinois J. Math., to appear.Google Scholar
Jaworski, W., Rosenblatt, J. M. and Willis, G. A.. Concentration functions in locally compact groups. Math. Ann. 305 (1996), 673–691.Google Scholar
Kaufman, R. and Rajagopalan, M.. On automorphisms of a locally compact group. Michigan Math. J. 13 (1966), 373–374.CrossRefGoogle Scholar
Kitchens, B.. Expansive dynamics of zero-dimensional groups. Ergod. Th. & Dynam. Sys. 7 (1987), 249–261.Google Scholar
Kitchens, B. and Schmidt, K.. Automorphisms of compact groups. Ergod. Th. & Dynam. Sys. 9 (1989), 691–735.Google Scholar
Kitchens, B. and Schmidt, K.. Isomorphism rigidity of irreducible ${ \mathbb{Z} }^{d} $-actions. Invent. Math. 142 (2000), 559–577.Google Scholar
Lang, S.. Algebra (Graduate Texts in Mathematics, 211), revised 3rd edn. Springer, New York, 2002.Google Scholar
Lind, D. and Schmidt, K.. Homoclinic points of algebraic ${ \mathbb{Z} }^{d} $-actions. J. Amer. Math. Soc. 12 (1999), 953–980.CrossRefGoogle Scholar
Montgomery, D. and Zippin, L.. Topological Transformation Groups. Interscience Publishers, New York, 1955.Google Scholar
Moore, C. C.. The Mautner phenomenon for general unitary representations. Pacific J. Math. 86 (1980), 155–169.CrossRefGoogle Scholar
Previts, W. H. and Wu, T.-S.. Dense orbits and compactness of groups. Bull. Austral. Math. Soc. 68 (1) (2003), 155–159.Google Scholar
Raja, C. R. E.. On the existence of ergodic automorphisms in ergodic ${ \mathbb{Z} }^{d} $-actions on compact groups. Ergod. Th. & Dynam. Sys. 30 (2010), 1803–1816.Google Scholar
Schmidt, K.. Dynamical Systems of Algebraic Origin (Progress in Mathematics, 128). Birkhäuser, Basel, 1995.Google Scholar
Siebert, E.. Contractive automorphisms on locally compact groups. Math. Z. 191 (1986), 73–90.Google Scholar
Tits, J.. Sur le groupe d’automorphismes d’un arbre. Essays on Topology and Related Topics (Memoires dédiés à Georges de Rham). Eds. Haeflinger, A. and Narisimhan, R.. Springer, New York, 1970, pp. 188–211.Google Scholar
Wang, J. S. P.. The Mautner phenomenon for $p$-adic Lie groups. Math. Z. 185 (1984), 403–412.Google Scholar
Willis, G. A.. The structure of totally disconnected, locally compact groups. Math. Ann. 300 (1994), 341–363.Google Scholar
Willis, G. A.. Totally disconnected groups and proofs of conjectures of Hofmann and Mukherjea. Bull. Austral. Math. Soc. 51 (1995), 489–494.Google Scholar
Willis, G. A.. Further properties of the scale function on a totally disconnected group. J. Algebra 237 (2001), 142–164.Google Scholar
Willis, G. A.. Tidy subgroups for commuting automorphisms of totally disconnected groups: an analogue of simultaneous triangularisation of matrices. New York J. Math. 10 (2004), 1–35; available at http://nyjm.albany.edu:8000/j/2004/Vol10.htm.Google Scholar
Willis, G. A.. A canonical form for automorphisms of totally disconnected locally compact groups. Random Walks and Geometry. Walter de Gruyter, Berlin, 2004, pp. 295–316.Google Scholar