Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-29T01:37:21.879Z Has data issue: false hasContentIssue false
  • English
  • Français

Normalisation holomorphe de structures de Poisson

Published online by Cambridge University Press:  17 July 2009

PHILIPP LOHRMANN
PHILIPP LOHRMANN*
Affiliation:
Institut für Mathematik, Universität Zürich, Winterthurerstrasse 190, 8057 Zürich, Switzerland (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that a Poisson structure whose linear part vanishes can be holomorphically normalized in a neighbourhood of its singular point 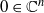if, on the one hand, a Diophantine condition on a Lie algebra associated to the quadratic part is satisfied and, on the other hand, the normal form satisfies some formal conditions.

Résumé

Nous montrons qu’une structure de Poisson à 1-jet nul est holomorphiquement conjuguée vers une forme normale au sens de Dufour–Wade, au voisinage de son point singulier 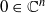, si sont vérifiées d’une part une condition diophantienne sur une algèbre de Lie associée à la partie quadratique, d’autre part certaines conditions sur la forme normale formelle.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 30 , Issue 4 , August 2010 , pp. 1165 - 1199
Copyright
Copyright © Cambridge University Press 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Arnol’d, V. I.. Mathematical Methods of Classical Mechanics, 2nd edn.(Graduate Texts in Mathematics, 60). Springer, Berlin, 1989.Google Scholar
[2]Bruno, A. D.. The analytical form of differential equations. Trans. Moscow Soc. 25 (1971), 131–288; 26 (1972), 199–239.Google Scholar
[3]Conn, J.. Normal forms for analytic Poisson structures. Ann. of Math. (2) 119 (1984), 577–601.Google Scholar
[4]Conn, J.. Correction to “Normal forms for analytic Poisson structures”. Ann. of Math. (2) 121 (1985), 433–436.Google Scholar
[5]Dufour, J. P. and Haraki, A.. Rotationnels et structures de Poisson quadratiques. C. R. Acad. Sci. Paris Sér. I 312 (1991), 137–140.Google Scholar
[6]Dufour, J. P. and Wade, A.. Formes normales de structures de Poisson ayant un 1-jet nul en un point. J. Geom. Phys. 26 (1998), 79–96.Google Scholar
[7]Dufour, J. P. and Zung, N. T.. Poisson Structures and their Normal Forms (Progress in Mathematics, 242). Birkhäuser, Basel, 2005.Google Scholar
[8]Stolovitch, L.. Singular complete integrability. Publ. Math. Inst. Hautes. Études. Sci. 91 (2000), 133–210.Google Scholar
[9]Stolovitch, L.. Sur les structures de Poisson singulières. Ergod. Th. & Dynam. Sys. 24(5) (2004), 1833–1863.Google Scholar
[10]Weinstein, A.. The local structure of Poisson manifolds. J. Differential Geom. 18 (1983), 523–557.CrossRefGoogle Scholar
[11]Wade, A.. Normalisation de structures de Poisson. PhD Thesis, Université Montpellier, 1996.Google Scholar