Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T04:20:33.927Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-standard smooth realizations of Liouville rotations

Published online by Cambridge University Press:  01 December 2007

B. R. FAYAD ,
M. SAPRYKINA  and
A. WINDSOR
B. R. FAYAD
Affiliation:
LAGA, UMR 7539, Université Paris 13, 93430 Villetaneuse, France (email: [email protected])
M. SAPRYKINA
Affiliation:
Department of Mathematics and Statistics, Jeffery Hall, University Avenue, Kingston, ON Canada, K7L 3N6 (email: [email protected])
A. WINDSOR
Affiliation:
Department of Mathematics, University of Texas at Austin, 1 University Station, C1200, Austin, TX 78712-0257, USA (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

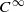We augment the conjugation approximation method with explicit estimates on the conjugacy map. This allows us to construct ergodic volume-preserving diffeomorphisms measure-theoretically isomorphic to any a priori given Liouville rotation on a variety of manifolds. In the special case of tori the maps can be made uniquely ergodic.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 27 , Issue 6 , December 2007 , pp. 1803 - 1818
Copyright
Copyright © Cambridge University Press 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Anosov, D. V. and Katok, A. B.. New examples in smooth ergodic theory. Ergodic diffeomorphisms. Tr. Mosk. Mat. Ob. 23 (1970), 3–36.Google Scholar
[2]Fayad, B. and Katok, A.. Constructions in elliptic dynamics. Ergod. Th. & Dynam. Sys. 24(5) (2004), 1477–1520.CrossRefGoogle Scholar
[3]Fayad, B. and Saprykina, M.. Weak mixing disc and annulus diffeomorphisms with arbitrary Liouville rotation number on the boundary. Ann. Sci. École Norm. Sup. (4) 38(3) (2005), 339–364.CrossRefGoogle Scholar
[4]Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia of Mathematics and its Applications, 54). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
[5]Saprykina, M.. Analytic nonlinearizable uniquely ergodic diffeomorphisms on . Ergod. Th. & Dynam. Sys. 23(3) (2003), 935–955.Google Scholar
[6]Windsor, A.. Minimal but not uniquely ergodic diffeomorphisms. Smooth Ergodic Theory and its Applications (Seattle, WA, 1999) (Proceedings Symposia in Pure Mathematics, 69). American Mathematical Society, Providence, RI, 2001, pp. 809–824.Google Scholar