No CrossRef data available.
Article contents
Non-singular 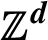 $\mathbb {Z}^d$-actions: an ergodic theorem over rectangles with application to the critical dimensions
$\mathbb {Z}^d$-actions: an ergodic theorem over rectangles with application to the critical dimensions
Published online by Cambridge University Press: 02 December 2020
Abstract
We adapt techniques developed by Hochman to prove a non-singular ergodic theorem for
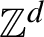 $\mathbb {Z}^d$
-actions where the sums are over rectangles with side lengths increasing at arbitrary rates, and in particular are not necessarily balls of a norm. This result is applied to show that the critical dimensions with respect to sequences of such rectangles are invariants of metric isomorphism. These invariants are calculated for the natural action of
$\mathbb {Z}^d$
-actions where the sums are over rectangles with side lengths increasing at arbitrary rates, and in particular are not necessarily balls of a norm. This result is applied to show that the critical dimensions with respect to sequences of such rectangles are invariants of metric isomorphism. These invariants are calculated for the natural action of
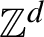 $\mathbb {Z}^d$
on a product of d measure spaces.
$\mathbb {Z}^d$
on a product of d measure spaces.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press



