A new mean ergodic theorem for tori and recurrences

Abstract

Let 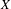$X$ be a finite-dimensional connected compact abelian group equipped with the normalized Haar measure $\unicode[STIX]{x1D707}$. We obtain the following mean ergodic theorem over ‘thin’ phase sets. Fix 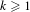$k\geq 1$ and, for every 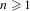$n\geq 1$, let 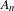$A_{n}$ be a subset of 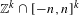$\mathbb{Z}^{k}\cap [-n,n]^{k}$. Assume that 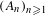$(A_{n})_{n\geq 1}$ has 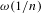$\unicode[STIX]{x1D714}(1/n)$ density in the sense that 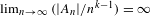$\lim _{n\rightarrow \infty }(|A_{n}|/n^{k-1})=\infty$. Let $T_{1},\ldots ,T_{k}$ be ergodic automorphisms of 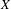$X$. We have

$$\begin{eqnarray}\frac{1}{|A_{n}|}\mathop{\sum }_{(n_{1},\ldots ,n_{k})\in A_{n}}f_{1}(T_{1}^{n_{1}}(x))\cdots f_{k}(T_{k}^{n_{k}}(x))\stackrel{L_{\unicode[STIX]{x1D707}}^{2}}{\longrightarrow }\int f_{1}\,d\unicode[STIX]{x1D707}\cdots \int f_{k}\,d\unicode[STIX]{x1D707},\end{eqnarray}$$

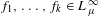for any $f_{1},\ldots ,f_{k}\in L_{\unicode[STIX]{x1D707}}^{\infty }$. When the 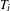$T_{i}$ are ergodic epimorphisms, the same conclusion holds under the further assumption that 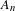$A_{n}$ is a subset of 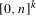$[0,n]^{k}$ for every $n$. The density assumption on the 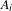$A_{i}$ is necessary. Immediate applications include certain Poincaré style recurrence results.