Hostname: page-component-6bf8c574d5-qdpjg Total loading time: 0 Render date: 2025-02-17T14:45:10.313Z Has data issue: false hasContentIssue false
  • English
  • Français

New examples of Bernoulli algebraic actions

Part of: Ergodic theory Topological dynamics

Published online by Cambridge University Press:  17 May 2021

DOUGLAS LIND Open the ORCID record for DOUGLAS LIND [Opens in a new window]  and
KLAUS SCHMIDT
DOUGLAS LIND*
Affiliation:
Department of Mathematics, University of Washington, Seattle, Washington98195, USA
KLAUS SCHMIDT
Affiliation:
Mathematics Institute, University of Vienna, Nordbergstrasse 15, A-1090Vienna, Austria (e-mail: [email protected])
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give an example of a principal algebraic action of the non-commutative free group 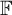${\mathbb {F}}$ of rank two by automorphisms of a connected compact abelian group for which there is an explicit measurable isomorphism with the full Bernoulli 3-shift action of ${\mathbb {F}}$ . The isomorphism is defined using homoclinic points, a method that has been used to construct symbolic covers of algebraic actions. To our knowledge, this is the first example of a Bernoulli algebraic action of 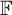${\mathbb {F}}$ without an obvious independent generator. Our methods can be generalized to a large class of acting groups.

Keywords

Bernoulli actionhomoclinic pointsymbolic coversofic group

MSC classification

Primary: 37A15: General groups of measure-preserving transformations 37A35: Entropy and other invariants, isomorphism, classification
Secondary: 37B10: Symbolic dynamics 37A20: Orbit equivalence, cocycles, ergodic equivalence relations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 9 , September 2022 , pp. 2923 - 2934
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution and reproduction, provided the original article is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press

References

Bowen, L.. Measure conjugacy invariants for actions of countable sofic groups. J. Amer. Math. Soc. 23 (2010), 217–245.CrossRefGoogle Scholar
Bowen, L.. Entropy for expansive algebraic actions of residually finite groups. Ergod. Th. & Dynam. Sys. 31 (2011), 703–718.CrossRefGoogle Scholar
Bowen, L.. Examples in the entropy theory of countable groups actions. Ergod. Th. & Dynam. Sys. 40 (2020), 2593–2680.Google Scholar
Chung, N.-P. and Li, H.. Homoclinic groups, IE groups, and expansive algebraic actions. Invent. Math. 199(3) (2015), 805–858.CrossRefGoogle Scholar
Deninger, C.. Fuglede-Kadison determinants and entropy for actions of discrete amenable groups. J. Amer. Math. Soc. 19(3) (2006), 737–758.CrossRefGoogle Scholar
Deninger, C. and Schmidt, K.. Expansive algebraic actions of discrete residually finite amenable groups and their entropy. Ergod. Th. & Dynam. Sys. 27(3) (2007), 769–786.CrossRefGoogle Scholar
Einsiedler, M. and Schmidt, K.. Markov partitions and homoclinic points of algebraic ${\mathbb{Z}}^d$ -actions. Tr. Mat. Inst. Steklova 216 (Din. Sist. i Smezhnye Vopr.) (1997), 265–284; Eng. transl. Proc. Steklov Inst. Math. 1(216) (1997), 259–279.Google Scholar
Halmos, P. R.. On automorphisms of compact groups. Bull. Amer. Math. Soc. 49 (1943), 619–624.CrossRefGoogle Scholar
Hayes, B.. Fuglede-Kadison determinants and sofic entropy. Geom. Funct. Anal. 26(2) (2016), 520–606.CrossRefGoogle Scholar
Hayes, B.. Max-min theorems for weak containment, square summable homoclinic points, and completely positive entropy. Preprint, 2019, arXiv:1902:06600v3.Google Scholar
Hayes, B.. Harmonic models and Bernoullicity. Preprint, 2020, arXiv:1904.03528v2.Google Scholar
Kerr, D.. Bernoulli actions of sofic groups have completely positive entropy. Israel J. Math. 202(1) (2014), 461–474.CrossRefGoogle Scholar
Kerr, D. and Li, H.. Ergodic Theory. Independence and Dichotomies (Springer Monographs in Mathematics). Springer, Cham, 2016.CrossRefGoogle Scholar
Kitchens, B. and Schmidt, K.. Automorphisms of compact groups. Ergod. Th. & Dynam. Sys. 9(4) (1989), 691–735.CrossRefGoogle Scholar
Lind, D. and Schmidt, K.. Homoclinic points of algebraic ${\mathbb{Z}}^d$ -actions. J. Amer. Math. Soc. 12(4) (1999), 953–980.CrossRefGoogle Scholar
Lind, D. and Schmidt, K.. A survey of algebraic actions of the discrete Heisenberg group. Uspekhi Mat. Nauk 70(4(424)) (2015), 77–142 (in Russian, with Russian summary); Eng. transl. Russian Math. Surveys 70(4) (2015), 57–714.Google Scholar
Lind, D., Schmidt, K. and Ward, T.. Mahler measure and entropy for commuting automorphisms of compact groups. Invent. Math. 101(3) (1990), 593–629.CrossRefGoogle Scholar
Lind, D. A.. The structure of skew products with ergodic group automorphisms. Israel J. Math. 28(3) (1977), 205–248.CrossRefGoogle Scholar
Miles, G. and Thomas, R. K.. Generalized torus automorphisms are Bernoullian. Studies in Probability and Ergodic Theory (Advances in Mathematics Supplementary Studies, 2). Academic Press, New York, 1978, pp. 231–249.Google Scholar
Ornstein, D. S. and Weiss, B.. Entropy and isomorphism theorems for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.CrossRefGoogle Scholar
Popa, S.. Some computations of 1-cohomology groups and construction of non-orbit-equivalent actions. J. Inst. Math. Jussieu 5(2) (2006), 309–332.CrossRefGoogle Scholar
Popa, S. and Sasyk, R.. On the cohomology of Bernoulli actions. Ergod. Th. & Dynam. Sys. 27(1) (2007), 241–251.CrossRefGoogle Scholar
Rudolph, D. J. and Schmidt, K.. Almost block independence and Bernoullicity of ${\mathbb{Z}}^d$ -actions by automorphisms of compact abelian groups. Invent. Math. 120(3) (1995), 455–488.CrossRefGoogle Scholar
Schmidt, K.. Dynamical Systems of Algebraic Origin (Progress in Mathematics, 128). Birkhäuser Verlag, Basel, 1995.Google Scholar