Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T05:43:40.694Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary and sufficient conditions for stable synchronization in random dynamical systems

Published online by Cambridge University Press:  24 January 2017

JULIAN NEWMAN Open the ORCID record for JULIAN NEWMAN [Opens in a new window]
JULIAN NEWMAN*
Affiliation:
Department of Mathematics, Imperial College London, South Kensington, London SW7 2AZ, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

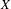For a composition of independent and identically distributed random maps or a memoryless stochastic flow on a compact space $X$, we find conditions under which the presence of locally asymptotically stable trajectories (e.g. as given by negative Lyapunov exponents) implies almost-sure mutual convergence of any given pair of trajectories (‘synchronization’). Namely, we find that synchronization occurs and is ‘stable’ if and only if the system exhibits the following properties: (i) there is a smallest non-empty invariant set 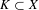$K\subset X$; (ii) any two points in 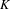$K$ are capable of being moved closer together; and (iii) 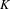$K$ admits asymptotically stable trajectories.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 5 , August 2018 , pp. 1857 - 1875
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonov, V. A.. Modeling of processes of cyclic evolution type. Synchronization by a random signal. Vestn. Leningr. Univ. Ser. Mat. Mekh. Astron. 2 (1984), 67–76.Google Scholar
Arnold, L.. Random Dynamical Systems (Springer Monographs in Mathematics) . Springer, Berlin, 1998.CrossRefGoogle Scholar
Baxendale, P. H.. Statistical equilibrium and two-point motion for a stochastic flow of diffeomorphisms. Spatial Stochastic Processes (Progress in Probability, 19) . Birkhäuser, Boston, 1991, pp. 189–218.Google Scholar
Baxendale, P. H. and Stroock, D. W.. Large deviations and stochastic flows of diffeomorphisms. Probab. Theory Related Fields 80(2) (1988), 169–215.Google Scholar
Carverhill, A.. Flows of stochastic dynamical systems: ergodic theory. Stochastics 14(4) (1985), 273–317.Google Scholar
Caraballo, T., Chueshov, I. and Kloeden, P.. Synchronization of a stochastic reaction-diffusion system on a thin two-layer domain. SIAM J. Math. Anal. 38(5) (2007), 1489–1507.Google Scholar
Crauel, H. and Flandoli, F.. Additive noise destroys a pitchfork bifurcation. J. Dynam. Differential Equations 10(2) (1998), 259–274.CrossRefGoogle Scholar
Crauel, H.. Invariant measures for random dynamical systems on the circle. Arch. Math. (Basel) 78(2) (2002), 145–154.CrossRefGoogle Scholar
Chueshov, I. and Scheutzow, M.. On the structure of attractors and invariant measures for a class of monotone random systems. Dyn. Syst. 19(2) (2004), 127–144.Google Scholar
Flandoli, F., Gess, B. and Scheutzow, M.. Synchronization by noise. Probab. Theory Related Fields (published online 3 May 2016), doi:10.1007/s00440-016-0716-2.Google Scholar
Flandoli, F., Gess, B. and Scheutzow, M.. Synchronization by noise for order-preserving random dynamical systems. Preprint, 2016, arXiv:1503.08737v2 [math.PR].Google Scholar
Homburg, A. J.. Synchronization in iterated function systems. Preprint, 2013, arXiv:1303.6054v1 [math.DS].Google Scholar
Kaijser, T.. On stochastic perturbations of iterations of circle maps. Phys. D 68(2) (1993), 201–231.Google Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems. Cambridge University Press, Cambridge, 1995.Google Scholar
Kifer, Y.. Ergodic Theory of Random Transformations. Birkhäuser, Boston, 1986.Google Scholar
Kleptsyn, V. A. and Nalskii, N. B.. Contraction of orbits in random dynamical systems on the circle. Funct. Anal. Appl. 38(4) (2004), 267–282.Google Scholar
Le Jan, Y.. Équilibre statistique pour les produits de difféomorphismes aléatoires indépendants. Ann. Inst. Henri Poincaré Probab. Stat. 23(1) (1987), 111–120.Google Scholar
Malicet, D.. Random walks on $\text{Homeo}(S^{1})$ . Preprint, 2014, arXiv:1412.8618v1 [math.DS].Google Scholar
Mohammed, S.-E. and Schuetzow, M.. The stable manifold theorem for stochastic differential equations. Ann. Probab. 27(2) (1999), 615–652.Google Scholar
Newman, J.. Ergodic theory for semigroups of Markov Kernels (5th July 2015). Seminar Notes, 2015, http://wwwf.imperial.ac.uk/∼jmn07/Ergodic_Theory_for_Semigroups_of_Markov_Kernels.pdf .Google Scholar
Ohno, T.. Asymptotic behaviors of dynamical systems with random parameters. Publ. Res. Inst. Math. Sci. 19(1) (1983), 83–98.Google Scholar
Pikovskii, A. S.. Synchronization and stochastization of array of self-excited oscillators by external noise. Radiophys. Quantum Electron. 27(5) (1984), 390–395.CrossRefGoogle Scholar
Toral, R., Mirasso, C. R., Hernandes-Garcia, E. and Piro, O.. Analytical and numerical studies of noise-induced synchronization of chaotic systems. Chaos 11(3) (2001), 665–673.CrossRefGoogle ScholarPubMed