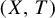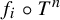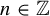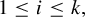1 Introduction
The multiplicity of an invertible bounded operator
![]() $U:E\circlearrowleft $
on a normed vector space E is the minimal cardinality of subsets
$U:E\circlearrowleft $
on a normed vector space E is the minimal cardinality of subsets
![]() $ F\subset E$
, whose cyclic space (that is, the vector space spanned by
$ F\subset E$
, whose cyclic space (that is, the vector space spanned by
![]() $U^kx$
,
$U^kx$
,
![]() $k\in {\mathbb {Z}}$
,
$k\in {\mathbb {Z}}$
,
![]() $x\in F$
) is dense in E.
$x\in F$
) is dense in E.
For an ergodic measure-preserving system
![]() $(X,f,{\mathcal B},\mu )$
, the multiplicity
$(X,f,{\mathcal B},\mu )$
, the multiplicity
![]() $\mathrm {Mult}(\mu )$
of the Koopman operator, which is the operator of composition by f on the Hilbert space
$\mathrm {Mult}(\mu )$
of the Koopman operator, which is the operator of composition by f on the Hilbert space
![]() $L^2(\mu )$
, is a dynamical invariant, which has been investigated in many works (see e.g. [Reference DanilenkoDan13] and the references therein).
$L^2(\mu )$
, is a dynamical invariant, which has been investigated in many works (see e.g. [Reference DanilenkoDan13] and the references therein).
Cyclicity, which corresponds to simple multiplicity (that is, there is an element whose cyclic space is dense in the whole vector space), has been also established for operators of composition on the Hardy space
![]() $H^2(D)$
[Reference Bourdon and ShapiroBS97]. In this context, a pioneering work of Birkhoff [Reference BirkhoffBir29] states that there is an entire function
$H^2(D)$
[Reference Bourdon and ShapiroBS97]. In this context, a pioneering work of Birkhoff [Reference BirkhoffBir29] states that there is an entire function
![]() $\phi $
in the complex plane such that the set
$\phi $
in the complex plane such that the set
![]() $\{\phi (\cdot +n), n\in \mathbb N\}$
is dense itself in the set of entire functions endowed with the uniform topology on compact subsets, that is, the operator of translation by
$\{\phi (\cdot +n), n\in \mathbb N\}$
is dense itself in the set of entire functions endowed with the uniform topology on compact subsets, that is, the operator of translation by
![]() $1$
is hypercyclic.
$1$
is hypercyclic.
Quite surprisingly, the corresponding topological invariant has not been studied in full generality. More precisely, we consider here topological dynamical systems
![]() $(X,T)$
, where X is a compact metrizable space and
$(X,T)$
, where X is a compact metrizable space and
![]() $T:X\circlearrowleft $
is a homeomorphism, and we study the operator of composition by T on the Banach space
$T:X\circlearrowleft $
is a homeomorphism, and we study the operator of composition by T on the Banach space
![]() $C(X)$
of real continuous functions endowed with the uniform topology. We call the topological multiplicity of
$C(X)$
of real continuous functions endowed with the uniform topology. We call the topological multiplicity of
![]() $(X,T)$
the associated multiplicity and we denote it by
$(X,T)$
the associated multiplicity and we denote it by
![]() $\mathrm {Mult}(T)$
. We remark that our definitions and results can be extended to the non-invertible continuous map
$\mathrm {Mult}(T)$
. We remark that our definitions and results can be extended to the non-invertible continuous map
![]() $T:X\circlearrowleft $
. However, for sake of simplicity, we focus on homeomorphisms
$T:X\circlearrowleft $
. However, for sake of simplicity, we focus on homeomorphisms
![]() $T:X\circlearrowleft $
.
$T:X\circlearrowleft $
.
In this paper, we mostly focus on topological systems with finite multiplicity. We first show the following properties for such systems.
Theorem. Let
![]() $(X,T)$
be a topological system with finite multiplicity. Then the following properties are satisfied:
$(X,T)$
be a topological system with finite multiplicity. Then the following properties are satisfied:
-
(1)
 $(X,T)$
has zero topological entropy;
$(X,T)$
has zero topological entropy; -
(2)
 $(X,T)$
has finitely many ergodic measures.
$(X,T)$
has finitely many ergodic measures.
These properties are the main content of §2. Property (1) is proven in Proposition 3.5 in two ways: one uses the variational principal of topological entropy; the other is purely topological. Property (2) is proven in Lemma 2.6 and Corollary 2.8. In fact, we show more precisely that the number of ergodic measures is equal to the multiplicity of the operator induced on the quotient of
![]() $C(X)$
by the closure of coboundaries.
$C(X)$
by the closure of coboundaries.
In §3, we relate the topological multiplicity with the dimension of cubical shifts, in which the action
![]() $T_*:{\mathcal M}(X)\circlearrowleft $
induced by T on the set
$T_*:{\mathcal M}(X)\circlearrowleft $
induced by T on the set
![]() ${\mathcal M}(X)$
of Borel probability measures on X may be affinely embedded. In Theorem 3.3, we show a necessary and sufficient condition for the existence of the affinely embedding of
${\mathcal M}(X)$
of Borel probability measures on X may be affinely embedded. In Theorem 3.3, we show a necessary and sufficient condition for the existence of the affinely embedding of
![]() $({\mathcal M}(X), T_*)$
to the shift on
$({\mathcal M}(X), T_*)$
to the shift on
![]() $([0,1]^d)^{\mathbb {Z}}$
. Furthermore, we compare our result to the Lindenstrauss–Tsukamoto conjecture for dynamical embedding (Corollary 3.4).
$([0,1]^d)^{\mathbb {Z}}$
. Furthermore, we compare our result to the Lindenstrauss–Tsukamoto conjecture for dynamical embedding (Corollary 3.4).
In §4, we state a generalized Banach version of a lemma due to Baxter [Reference BaxterBax71] which is a classical criterion of simplicity for ergodic transformations. The generalized Baxter lemma (Lemma 4.1) will play an important role in estimating the topological multiplicity in the next sections.
For minimal Cantor systems, a topological analogue of the rank of a measure-preserving system has been defined and studied (see [Reference Durand and PerrinDP22]). In §5, under this setting, we compare the topological multiplicity with the topological rank (Theorem 5.1).
In §6, we study some examples and estimate their topological multiplicity: minimal rotations on compact groups, Sturmian and Thue–Morse subshifts, homeomorphisms of the interval, etc. Among them, we show in Theorem 6.7 that even though the Thue–Morse subshift is a minimal uniquely ergodic system with simple mixed spectrum, its topological multiplicity is one.
Theorem. The Thue–Morse subshift has simple topological spectrum.
In §6, we estimate the topological multiplicity of subshifts with linear growth complexity, that is, subshifts X such that the cardinality
![]() $p_X(n)$
of n-words in X satisfies
$p_X(n)$
of n-words in X satisfies
![]() $\liminf _{n\to \infty }({p_X(n)}/{n})<+\infty $
. Such subshifts have aroused a great deal of interest, especially recently [Reference BoshernitzanBos92, Reference Cyr and KraCK19, Reference Creutz and PavlovCP23, Reference Donoso, Durand, Maass and PetiteDDMP21]. In [Reference BoshernitzanBos92], it is proved that an aperiodic subshift X has at most k ergodic measures if
$\liminf _{n\to \infty }({p_X(n)}/{n})<+\infty $
. Such subshifts have aroused a great deal of interest, especially recently [Reference BoshernitzanBos92, Reference Cyr and KraCK19, Reference Creutz and PavlovCP23, Reference Donoso, Durand, Maass and PetiteDDMP21]. In [Reference BoshernitzanBos92], it is proved that an aperiodic subshift X has at most k ergodic measures if
![]() $\liminf _n({p_X(n)}/{n})\leq k\in \mathbb N$
. Our main related result is stated as follows (Theorems 7.1 and 7.6).
$\liminf _n({p_X(n)}/{n})\leq k\in \mathbb N$
. Our main related result is stated as follows (Theorems 7.1 and 7.6).
Theorem. Let X be an aperiodic subshift with
![]() $\liminf _{n\to \infty }({p_X(n)}/{n})\leq k\in \mathbb N$
. Then
$\liminf _{n\to \infty }({p_X(n)}/{n})\leq k\in \mathbb N$
. Then
 $$ \begin{align*}\mathrm{Mult}(T)\leq 2k \quad\text{and}\quad\sum_{\mu \ \mathrm{ergodic}} \mathrm{ Mult}(\mu)\leq 2k.\end{align*} $$
$$ \begin{align*}\mathrm{Mult}(T)\leq 2k \quad\text{and}\quad\sum_{\mu \ \mathrm{ergodic}} \mathrm{ Mult}(\mu)\leq 2k.\end{align*} $$
As well as the results on multiplicity that we investigate, we propose several questions in the current paper.
2 Topological multiplicity, definition, and first properties
2.1 Multiplicity of a linear operator
Let
![]() $(E,\|\cdot \|)$
be a normed vector space over
$(E,\|\cdot \|)$
be a normed vector space over
![]() $\mathbb R$
. We consider a linear invertible bounded operator
$\mathbb R$
. We consider a linear invertible bounded operator
![]() $U:E\circlearrowleft $
. A subset F of E is called a generating family of U when the vector space spanned by
$U:E\circlearrowleft $
. A subset F of E is called a generating family of U when the vector space spanned by
![]() $U^kx$
,
$U^kx$
,
![]() $k\in {\mathbb {Z}}$
,
$k\in {\mathbb {Z}}$
,
![]() $x\in F$
, is dense in E. In the following, we denote by
$x\in F$
, is dense in E. In the following, we denote by
![]() $\text {span}(G)$
(respectively
$\text {span}(G)$
(respectively
![]() $\overline {\text {span}}(G)$
) the vector space spanned by a subset G of E (respectively its closure) and we then let
$\overline {\text {span}}(G)$
) the vector space spanned by a subset G of E (respectively its closure) and we then let
![]() $V^U_F:=\overline {\text {span}}\{ U^k x: k \in \mathbb {Z}, x\in F \}$
. Sometimes, we write
$V^U_F:=\overline {\text {span}}\{ U^k x: k \in \mathbb {Z}, x\in F \}$
. Sometimes, we write
![]() $V_F$
instead of
$V_F$
instead of
![]() $V^U_F$
whenever the operator is fixed. The multiplicity
$V^U_F$
whenever the operator is fixed. The multiplicity
![]() $\mathrm {Mult}(U)\in \mathbb N\cup \{\infty \}$
of U is then the smallest cardinality of generating families of U. By convention, we let
$\mathrm {Mult}(U)\in \mathbb N\cup \{\infty \}$
of U is then the smallest cardinality of generating families of U. By convention, we let
![]() $\mathrm {Mult}(U)=0$
when E is reduced to
$\mathrm {Mult}(U)=0$
when E is reduced to
![]() $\{0\}$
. A linear operator with multiplicity one is called cyclic.
$\{0\}$
. A linear operator with multiplicity one is called cyclic.
We first study the equivariant map between two normed vector spaces with linear invertible bounded operators.
Lemma 2.1. Let
![]() $U_i:E_i\circlearrowleft $
,
$U_i:E_i\circlearrowleft $
,
![]() $i=1,2$
be two linear invertible bounded operators. Assume that there is a linear bounded operator
$i=1,2$
be two linear invertible bounded operators. Assume that there is a linear bounded operator
![]() $W:E_1\rightarrow E_2$
satisfying
$W:E_1\rightarrow E_2$
satisfying
![]() $W\circ U_1=U_2\circ W$
, then
$W\circ U_1=U_2\circ W$
, then
Proof. One checks easily that if F is a generating family for
![]() $U_1$
, then
$U_1$
, then
![]() $W(F)$
is a generating family for the restriction of
$W(F)$
is a generating family for the restriction of
![]() $U_2$
to the closure of the image of W. Therefore,
$U_2$
to the closure of the image of W. Therefore,
![]() $\mathrm {Mult}(U_2|_{\overline {\mathrm {Im}(W)}})\leq \mathrm {Mult}(U_1)$
.
$\mathrm {Mult}(U_2|_{\overline {\mathrm {Im}(W)}})\leq \mathrm {Mult}(U_1)$
.
A direct consequence of Lemma 2.1 is that the multiplicity is a spectral invariant: if
![]() $U_i$
are linear invertible operators on
$U_i$
are linear invertible operators on
![]() $E_i,i=1,2$
, satisfying
$E_i,i=1,2$
, satisfying
![]() $W\circ U_1=U_2\circ W$
for some invertible bounded linear operator
$W\circ U_1=U_2\circ W$
for some invertible bounded linear operator
![]() $W:E_1\rightarrow E_2$
, then
$W:E_1\rightarrow E_2$
, then
![]() $U_1$
and
$U_1$
and
![]() $U_2$
have the same multiplicities.
$U_2$
have the same multiplicities.
When
![]() $E'$
is a closed subspace of E, we endow the quotient
$E'$
is a closed subspace of E, we endow the quotient
![]() $E/E'$
space with the norm
$E/E'$
space with the norm
![]() $\|\overline {u}\|'=\inf \{\|u+v\|, v\in E' \}$
. If
$\|\overline {u}\|'=\inf \{\|u+v\|, v\in E' \}$
. If
![]() $E'$
is invariant by U, we let
$E'$
is invariant by U, we let
![]() $U^{E/E'}$
be the action induced by U on the quotient normed space
$U^{E/E'}$
be the action induced by U on the quotient normed space
![]() $E/E'$
. In this context, by applying Lemma 2.1 with
$E/E'$
. In this context, by applying Lemma 2.1 with
![]() $W:E\rightarrow E/E'$
being the natural projection, we get
$W:E\rightarrow E/E'$
being the natural projection, we get
2.2 Operator of composition: topological and ergodic multiplicities
Ergodic theory focuses on the study of invertible measure-preserving systems
![]() $(X,f,{\mathcal B}, \mu )$
. In particular, the spectral properties of the unitary operator
$(X,f,{\mathcal B}, \mu )$
. In particular, the spectral properties of the unitary operator
![]() $U_f:L^2(\mu )\circlearrowleft $
,
$U_f:L^2(\mu )\circlearrowleft $
,
![]() $\phi \mapsto \phi \circ f$
, are investigated. We let
$\phi \mapsto \phi \circ f$
, are investigated. We let
![]() $\|f\|_{2}:=(\int _X|f(x)|^2\, d\mu )^{1/2}$
be the
$\|f\|_{2}:=(\int _X|f(x)|^2\, d\mu )^{1/2}$
be the
![]() $L^2$
-norm of
$L^2$
-norm of
![]() $f\in L^2(\mu )$
.
$f\in L^2(\mu )$
.
Definition 2.2. The ergodic multiplicity
![]() $\mathrm {Mult}(\mu )$
of an ergodic system
$\mathrm {Mult}(\mu )$
of an ergodic system
![]() $(X,f,{\mathcal B}, \mu )$
is the multiplicity of the restriction of
$(X,f,{\mathcal B}, \mu )$
is the multiplicity of the restriction of
![]() $U_f$
to the Hilbert space
$U_f$
to the Hilbert space
![]() $L_0^2(\mu ):=\{f\in L^2(\mu ), \int f d\mu =0\}$
, that is to say,
$L_0^2(\mu ):=\{f\in L^2(\mu ), \int f d\mu =0\}$
, that is to say,
![]() $\mathrm {Mult}(\mu )=\mathrm {Mult}(U_f)$
.
$\mathrm {Mult}(\mu )=\mathrm {Mult}(U_f)$
.
This quantity has been intensely studied in ergodic theory (see Danilenko’s survey [Reference DanilenkoDan13]).
Next we consider here an invertible topological dynamical system
![]() $(X,T)$
, that is,
$(X,T)$
, that is,
![]() $T:X\circlearrowleft $
is a homeomorphism of a compact metric space X. We denote by
$T:X\circlearrowleft $
is a homeomorphism of a compact metric space X. We denote by
![]() $C(X)$
the Banach space of real continuous functions endowed with the topology of uniform convergence. We let
$C(X)$
the Banach space of real continuous functions endowed with the topology of uniform convergence. We let
![]() $\|f\|_{\infty }:=\sup _{x\in X}|f(x)|$
be the supremum norm of
$\|f\|_{\infty }:=\sup _{x\in X}|f(x)|$
be the supremum norm of
![]() $f\in C(X)$
.
$f\in C(X)$
.
Definition 2.3. The topological multiplicity
![]() $\mathrm {Mult}(T)$
of
$\mathrm {Mult}(T)$
of
![]() $(X,T)$
is the multiplicity of the operator of composition
$(X,T)$
is the multiplicity of the operator of composition
![]() $U_T:C(X)\circlearrowleft $
,
$U_T:C(X)\circlearrowleft $
,
![]() $\phi \mapsto \phi \circ T$
.
$\phi \mapsto \phi \circ T$
.
Quite surprisingly, this last notion seems to be new (note however that cyclicity of
![]() $U_T$
has already been investigated in some cases). Let us first observe that the topological multiplicity bounds from above the ergodic multiplicity of ergodic T-invariant measures.
$U_T$
has already been investigated in some cases). Let us first observe that the topological multiplicity bounds from above the ergodic multiplicity of ergodic T-invariant measures.
Lemma 2.4. Let
![]() $(X,T)$
be an invertible topological dynamical system. For any ergodic T-invariant measure
$(X,T)$
be an invertible topological dynamical system. For any ergodic T-invariant measure
![]() $\mu $
, we have
$\mu $
, we have
Proof. Let F be a generating family with minimal cardinality of
![]() $U_T:C(X)\circlearrowleft $
. Then the vector space spanned by F is dense in
$U_T:C(X)\circlearrowleft $
. Then the vector space spanned by F is dense in
![]() $(C(X),\|\cdot \|_{\infty })$
, therefore in
$(C(X),\|\cdot \|_{\infty })$
, therefore in
![]() $(L^2(\mu ),\|\cdot \|_2)$
. As
$(L^2(\mu ),\|\cdot \|_2)$
. As
![]() $p:L^2(\mu )\rightarrow L^2_0(\mu )$
,
$p:L^2(\mu )\rightarrow L^2_0(\mu )$
,
![]() $f\mapsto f-\int f\ d\mu $
is continuous and
$f\mapsto f-\int f\ d\mu $
is continuous and
![]() $p\circ U_T=U_T\circ p$
, the vector space spanned by
$p\circ U_T=U_T\circ p$
, the vector space spanned by
![]() $p(F)$
is dense in
$p(F)$
is dense in
![]() $L^2_0(\mu )$
.
$L^2_0(\mu )$
.
Let
![]() ${\mathcal M}(X)$
be the set of Borel probability measures endowed with the weak-
${\mathcal M}(X)$
be the set of Borel probability measures endowed with the weak-
![]() $*$
topology. It is standard that
$*$
topology. It is standard that
![]() ${\mathcal M}(X)$
is a compact metrizable space. The compact subset
${\mathcal M}(X)$
is a compact metrizable space. The compact subset
![]() ${\mathcal M}(X,T)\subset {\mathcal M}(X)$
of Borel T-invariant probability measures of
${\mathcal M}(X,T)\subset {\mathcal M}(X)$
of Borel T-invariant probability measures of
![]() $(X,T)$
is a simplex, whose extreme set is given by the subset
$(X,T)$
is a simplex, whose extreme set is given by the subset
![]() ${\mathcal M}_e(X,T)$
of ergodic measures. A topological system with a unique (ergodic) invariant measure is said to be uniquely ergodic. The Jewett–Krieger theorem states that every ergodic system has a uniquely ergodic model. Several proofs have been given of this theorem, see, e.g., [Reference Denker, Grillenberger and SigmundDGS06, §29]. One may wonder if the multiplicity may be preserved.
${\mathcal M}_e(X,T)$
of ergodic measures. A topological system with a unique (ergodic) invariant measure is said to be uniquely ergodic. The Jewett–Krieger theorem states that every ergodic system has a uniquely ergodic model. Several proofs have been given of this theorem, see, e.g., [Reference Denker, Grillenberger and SigmundDGS06, §29]. One may wonder if the multiplicity may be preserved.
Question 2.5. Given an ergodic system with measure
![]() $\mu $
, is there a uniquely ergodic model
$\mu $
, is there a uniquely ergodic model
![]() $(X,T)$
of it such that
$(X,T)$
of it such that
![]() $\mathrm {Mult}(T)=\mathrm {Mult}(\mu )$
?
$\mathrm {Mult}(T)=\mathrm {Mult}(\mu )$
?
2.3 The number of ergodic measures as a multiplicity
Let
![]() $(X,T)$
be an invertible topological dynamical system. A function
$(X,T)$
be an invertible topological dynamical system. A function
![]() $\psi \in C(X)$
is a called a continuous T-coboundary, if
$\psi \in C(X)$
is a called a continuous T-coboundary, if
![]() $\psi $
is equal to
$\psi $
is equal to
![]() $\phi \circ T-\phi $
for some
$\phi \circ T-\phi $
for some
![]() $\phi \in C(X)$
. In other terms, the set
$\phi \in C(X)$
. In other terms, the set
![]() $B_T(X)$
of continuous T-coboundaries is the image of
$B_T(X)$
of continuous T-coboundaries is the image of
![]() $U_T-\mathrm {Id}$
, in particular, it is a vector space. Observe that
$U_T-\mathrm {Id}$
, in particular, it is a vector space. Observe that
![]() $U_T(B_T(X))= B_T(X)$
. To simplify the notation, we write
$U_T(B_T(X))= B_T(X)$
. To simplify the notation, we write
![]() $\tilde {U}_T$
for the action induced by
$\tilde {U}_T$
for the action induced by
![]() $U_T$
on the quotient Banach space
$U_T$
on the quotient Banach space
![]() $C(X)/ \overline {B_T(X)}$
and
$C(X)/ \overline {B_T(X)}$
and
![]() $\underline {U}_T$
for the restriction of
$\underline {U}_T$
for the restriction of
![]() $U_T$
to the closure
$U_T$
to the closure
![]() $\overline {B_T(X)}$
of continuous coboundaries. By a standard application of the Hahn–Banach theorem (see e.g. [Reference KatokKat01, Proposition 2.13]), a function
$\overline {B_T(X)}$
of continuous coboundaries. By a standard application of the Hahn–Banach theorem (see e.g. [Reference KatokKat01, Proposition 2.13]), a function
![]() $\psi $
belongs to
$\psi $
belongs to
![]() $\overline {B_T(X)}$
if and only if
$\overline {B_T(X)}$
if and only if
![]() $\int \psi \, d\mu =0$
for any
$\int \psi \, d\mu =0$
for any
![]() $\mu \in {\mathcal M}(X,T)$
(respectively
$\mu \in {\mathcal M}(X,T)$
(respectively
![]() $\mu \in {\mathcal M}_e(X,T)$
). It is well known that unique ergodicity is equivalent to the decomposition
$\mu \in {\mathcal M}_e(X,T)$
). It is well known that unique ergodicity is equivalent to the decomposition ![]() (see e.g. [Reference Liardet and VolnLV97, Lemma 1]), where
(see e.g. [Reference Liardet and VolnLV97, Lemma 1]), where ![]() denotes the constant function equal to
denotes the constant function equal to
![]() $1$
. In particular, in the case of unique ergodicity, we have
$1$
. In particular, in the case of unique ergodicity, we have ![]() and therefore
and therefore
![]() $\mathrm {Mult}(\tilde U_T)=1$
. It may be generalized as follows.
$\mathrm {Mult}(\tilde U_T)=1$
. It may be generalized as follows.
Lemma 2.6. Let
![]() $(X,T)$
be an invertible topological dynamical system. We have
$(X,T)$
be an invertible topological dynamical system. We have
Proof. We first show that
![]() $\mathrm {Mult}(\tilde U_T)\geq \sharp {\mathcal M}_e(X,T)$
. Assume that:
$\mathrm {Mult}(\tilde U_T)\geq \sharp {\mathcal M}_e(X,T)$
. Assume that:
-
•
 $\nu _1,\ldots , \nu _p$
are distinct ergodic measures;
$\nu _1,\ldots , \nu _p$
are distinct ergodic measures; -
•
 $\overline {F}=\{\overline {f_1}, \ldots , \overline {f_q}\}\in C(X)/ \overline {B_T(X)} $
is a generating family of
$\overline {F}=\{\overline {f_1}, \ldots , \overline {f_q}\}\in C(X)/ \overline {B_T(X)} $
is a generating family of
 $\tilde {U}_T$
.
$\tilde {U}_T$
.
For
![]() $1\le l\le q$
, let
$1\le l\le q$
, let
![]() $f_l\in C(X)$
be a function (a priori not unique) such that
$f_l\in C(X)$
be a function (a priori not unique) such that
![]() $\overline {f_l} = f_l \mod \overline {B_T(X)}$
. If
$\overline {f_l} = f_l \mod \overline {B_T(X)}$
. If
![]() $q<p$
, then the p vectors
$q<p$
, then the p vectors
 $$ \begin{align*} X_i=\bigg(\int f_l\, d\nu_i\bigg)_{l=1, 2, \ldots, q},\quad i=1, 2,\ldots, p, \end{align*} $$
$$ \begin{align*} X_i=\bigg(\int f_l\, d\nu_i\bigg)_{l=1, 2, \ldots, q},\quad i=1, 2,\ldots, p, \end{align*} $$
are linearly dependent in
![]() $\mathbb {R}^q$
, that is, there is
$\mathbb {R}^q$
, that is, there is
![]() $(c_i)_{1\le i\le p}\in \mathbb R^{p} \setminus (0,0, \ldots , 0)$
such that
$(c_i)_{1\le i\le p}\in \mathbb R^{p} \setminus (0,0, \ldots , 0)$
such that
 $$ \begin{align} \sum_{1\le i\le p}c_iX_i &=0. \end{align} $$
$$ \begin{align} \sum_{1\le i\le p}c_iX_i &=0. \end{align} $$
Let
![]() $\nu $
be the signed measure
$\nu $
be the signed measure
![]() $\nu =\sum _{1\le i\le p}c_i\nu _i$
. Then equation (2.2) may be rewritten as
$\nu =\sum _{1\le i\le p}c_i\nu _i$
. Then equation (2.2) may be rewritten as
The measures
![]() $\nu _i$
are invariant for
$\nu _i$
are invariant for
![]() ${1\le i\le p}$
, so is
${1\le i\le p}$
, so is
![]() $\nu $
. Therefore, we get
$\nu $
. Therefore, we get
However,
![]() $V^{\tilde {U}_T}_{\overline {F}}=C(X)/ \overline {B_T(X)}$
, so that for any
$V^{\tilde {U}_T}_{\overline {F}}=C(X)/ \overline {B_T(X)}$
, so that for any
![]() $\epsilon>0$
and for any
$\epsilon>0$
and for any
![]() $g\in C(X)$
, we may find
$g\in C(X)$
, we may find
![]() $h \in \mathrm {span}(f_l\circ T^k, 1\le l\le q,k\in \mathbb {Z})$
and
$h \in \mathrm {span}(f_l\circ T^k, 1\le l\le q,k\in \mathbb {Z})$
and
![]() $u\in B_T(X)$
with
$u\in B_T(X)$
with
![]() $\|g-(h+u)\|_{\infty }<\epsilon $
. By equation (2.3), we have
$\|g-(h+u)\|_{\infty }<\epsilon $
. By equation (2.3), we have
![]() $\int h\, d\nu =0$
. As u is a coboundary, we have also
$\int h\, d\nu =0$
. As u is a coboundary, we have also
![]() $\int u\, d\nu =0$
. Therefore,
$\int u\, d\nu =0$
. Therefore,
 $$ \begin{align*}\bigg|\int g\, d\nu\bigg|&\leq \bigg|\int (h+u)\, d\nu\bigg|+\|g-(h+u)\|_{\infty}<\epsilon. \end{align*} $$
$$ \begin{align*}\bigg|\int g\, d\nu\bigg|&\leq \bigg|\int (h+u)\, d\nu\bigg|+\|g-(h+u)\|_{\infty}<\epsilon. \end{align*} $$
Since
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $g\in C(X)$
are chosen arbitrarily, we obtain
$g\in C(X)$
are chosen arbitrarily, we obtain
![]() $\int g\, d\nu =0$
, for any
$\int g\, d\nu =0$
, for any
![]() $g\in C(X)$
, therefore,
$g\in C(X)$
, therefore,
![]() $\nu =0$
. This contradicts the ergodicity of the measures
$\nu =0$
. This contradicts the ergodicity of the measures
![]() $\nu _i$
for
$\nu _i$
for
![]() $1\le i\le p$
. Consequently, we have
$1\le i\le p$
. Consequently, we have
![]() $q\geq p$
and, therefore,
$q\geq p$
and, therefore,
![]() $\mathrm {Mult}(\tilde U_T)\geq \sharp {\mathcal M}_e(X,T)$
.
$\mathrm {Mult}(\tilde U_T)\geq \sharp {\mathcal M}_e(X,T)$
.
Let us show now the converse inequality. Without loss of generality, we may assume that
![]() $p=\sharp {\mathcal M}_e(X,T)< \mathrm {Mult}(\tilde {U}_T)=q<\infty $
. We let again:
$p=\sharp {\mathcal M}_e(X,T)< \mathrm {Mult}(\tilde {U}_T)=q<\infty $
. We let again:
-
•
 ${\mathcal M}_e(X,T)=\{\nu _1,\ldots , \nu _p\}$
;
${\mathcal M}_e(X,T)=\{\nu _1,\ldots , \nu _p\}$
; -
•
 $\overline {F}={\overline {f_1}, \ldots , \overline {f_q}}\in C(X)/ \overline {B_T(X)} $
a generating family of
$\overline {F}={\overline {f_1}, \ldots , \overline {f_q}}\in C(X)/ \overline {B_T(X)} $
a generating family of
 $\tilde {U}_T$
with minimal cardinality.
$\tilde {U}_T$
with minimal cardinality.
Then the q vectors
 $$ \begin{align*} Y_l=\bigg(\int f_l\,d\nu_i\bigg)_{i=1,\ldots, p}, \quad l=1,\ldots, q, \end{align*} $$
$$ \begin{align*} Y_l=\bigg(\int f_l\,d\nu_i\bigg)_{i=1,\ldots, p}, \quad l=1,\ldots, q, \end{align*} $$
are linearly dependent in
![]() $\mathbb {R}^p$
, that is, there is
$\mathbb {R}^p$
, that is, there is
![]() $(c_l)_{1\le l\le q}\in \mathbb R^{q}\setminus (0,0 \ldots , 0)$
such that
$(c_l)_{1\le l\le q}\in \mathbb R^{q}\setminus (0,0 \ldots , 0)$
such that
 $$ \begin{align*} \sum_{1\le l\le q}c_lY_l=0. \end{align*} $$
$$ \begin{align*} \sum_{1\le l\le q}c_lY_l=0. \end{align*} $$
Let g be the function
![]() $g=\sum _{1\le l\le q}c_lf_l$
. Then we have
$g=\sum _{1\le l\le q}c_lf_l$
. Then we have
As previously mentioned, it implies that g lies in
![]() $\overline {B_T(X)}$
. This contradicts the minimality of the generating family
$\overline {B_T(X)}$
. This contradicts the minimality of the generating family
![]() $\overline {F}$
.
$\overline {F}$
.
Remark 2.7. It follows from the proof of Lemma 2.6 that if
![]() ${{\mathcal M}}_e(X,T)=\{\nu _1,\ldots , \nu _p\}$
, then
${{\mathcal M}}_e(X,T)=\{\nu _1,\ldots , \nu _p\}$
, then
![]() ${\overline {f_1}, \ldots , \overline {f_p}}$
is a generating family of
${\overline {f_1}, \ldots , \overline {f_p}}$
is a generating family of
![]() $\tilde {U}_T$
if and only if the matrix
$\tilde {U}_T$
if and only if the matrix
![]() $A=(\int f_j\,d\nu _i)_{1\le i,j\le p}\in M_p(\mathbb R)$
is invertible.
$A=(\int f_j\,d\nu _i)_{1\le i,j\le p}\in M_p(\mathbb R)$
is invertible.
By equation (2.1) and Lemma 2.6, we get the following corollary.
Corollary 2.8.
2.4 Relating
 $\mathrm {Mult}(T)$
and
$\mathrm {Mult}(T)$
and
 $\mathrm {Mult}(\underline {U}_T)$
$\mathrm {Mult}(\underline {U}_T)$
It follows from the definition of
![]() $\overline {B_T(X)}$
that the map
$\overline {B_T(X)}$
that the map
has dense image and commutes with
![]() $U_T$
. By applying Lemma 2.1 with
$U_T$
. By applying Lemma 2.1 with
![]() $U_1=U_2=U$
and
$U_1=U_2=U$
and
![]() $E_1=C(X)$
,
$E_1=C(X)$
,
![]() $E_2=\overline {B_T(X)}$
, we obtain
$E_2=\overline {B_T(X)}$
, we obtain
![]() $\mathrm { Mult}(\underline {U}_T)\leq \mathrm {Mult}(T)$
.
$\mathrm { Mult}(\underline {U}_T)\leq \mathrm {Mult}(T)$
.
We show then in this subsection the following inequality.
Proposition 2.9.
In particular, if
![]() $(X,T)$
is uniquely ergodic,
$(X,T)$
is uniquely ergodic,
![]() $\mathrm {Mult}(T)=\mathrm {Mult}(\underline {U}_T)$
by Lemma 2.6. Let us now prove Proposition 2.9. For a family F of
$\mathrm {Mult}(T)=\mathrm {Mult}(\underline {U}_T)$
by Lemma 2.6. Let us now prove Proposition 2.9. For a family F of
![]() $C(X)$
, we write
$C(X)$
, we write
![]() $\overline {F}$
the subset of
$\overline {F}$
the subset of
![]() $C(X)/\overline {B_T(X)}$
consisting of
$C(X)/\overline {B_T(X)}$
consisting of
![]() $\overline {f}= f \mod \overline {B_T(X)}$
for
$\overline {f}= f \mod \overline {B_T(X)}$
for
![]() $f\in F$
. We start with a technical lemma.
$f\in F$
. We start with a technical lemma.
Lemma 2.10. Let
![]() $(X,T)$
be an invertible dynamical system with
$(X,T)$
be an invertible dynamical system with
![]() $\sharp {\mathcal M}_e(X,T)< \infty $
. If F is a family of
$\sharp {\mathcal M}_e(X,T)< \infty $
. If F is a family of
![]() $C(X)$
such that
$C(X)$
such that
![]() $\overline F$
is generating for
$\overline F$
is generating for
![]() $\tilde {U}_T$
, then the constant function
$\tilde {U}_T$
, then the constant function ![]() belongs to
belongs to
![]() $V_F$
.
$V_F$
.
Proof. Let
![]() ${\mathcal M}_e(X, T)=\{\nu _1,\ldots ,\nu _p\}$
. By Remark 2.7, the matrix
${\mathcal M}_e(X, T)=\{\nu _1,\ldots ,\nu _p\}$
. By Remark 2.7, the matrix
![]() $(\int f_i\,d\nu _j)_{1\le i,j\le p}$
is invertible. Then by replacing
$(\int f_i\,d\nu _j)_{1\le i,j\le p}$
is invertible. Then by replacing
![]() $F=\{f_1,\ldots , f_p\}$
by some invertible linear combinations, we can assume
$F=\{f_1,\ldots , f_p\}$
by some invertible linear combinations, we can assume
where
![]() $\delta _{i,j}$
is equal to
$\delta _{i,j}$
is equal to
![]() $1$
if
$1$
if
![]() $i=j$
and
$i=j$
and
![]() $0$
otherwise. Let
$0$
otherwise. Let
![]() $f=\sum _{i=1}^p f_i$
. We have
$f=\sum _{i=1}^p f_i$
. We have
 $$ \begin{align} \text{ for all } 1\leq j\leq p,\quad &\int f \, d\nu_j=\sum_i\delta_{i,j}=1,\nonumber\\[-3pt]\text{and, therefore, for all } \nu\in \mathcal{M}(X, T),\quad& \int f \, d\nu=1. \end{align} $$
$$ \begin{align} \text{ for all } 1\leq j\leq p,\quad &\int f \, d\nu_j=\sum_i\delta_{i,j}=1,\nonumber\\[-3pt]\text{and, therefore, for all } \nu\in \mathcal{M}(X, T),\quad& \int f \, d\nu=1. \end{align} $$
We claim that
![]() $({1}/{N}) \sum _{n=0}^{N-1} f\circ T^n$
is converging uniformly to
$({1}/{N}) \sum _{n=0}^{N-1} f\circ T^n$
is converging uniformly to ![]() as N goes to infinity. If not, there would exist a positive number
as N goes to infinity. If not, there would exist a positive number
![]() $\epsilon $
, a sequence
$\epsilon $
, a sequence
![]() $(x_k)_{k\ge 1}$
, and an increasing sequence
$(x_k)_{k\ge 1}$
, and an increasing sequence
![]() $(N_k)_{k\ge 1}$
of positive integers such that
$(N_k)_{k\ge 1}$
of positive integers such that
 $$ \begin{align} \bigg| \frac{1}{N_k} \sum_{n=0}^{N_k-1} f(T^n(x_k)) -1 \bigg|>\epsilon \quad \text{for all } k\ge 1. \end{align} $$
$$ \begin{align} \bigg| \frac{1}{N_k} \sum_{n=0}^{N_k-1} f(T^n(x_k)) -1 \bigg|>\epsilon \quad \text{for all } k\ge 1. \end{align} $$
After passing to a subsequence of
![]() $(N_k)_{k\ge 1}$
, we might assume that
$(N_k)_{k\ge 1}$
, we might assume that
![]() $({1}/{N_k}) \sum _{n=0}^{N_k-1} \delta _{T^n(x_k)}$
is converging to a T-invariant measure
$({1}/{N_k}) \sum _{n=0}^{N_k-1} \delta _{T^n(x_k)}$
is converging to a T-invariant measure
![]() $\mu $
in the weak-
$\mu $
in the weak-
![]() $*$
topology. It follows from equation (2.5) that
$*$
topology. It follows from equation (2.5) that
 $$ \begin{align*} \bigg| \int f d\mu -1 \bigg|>\epsilon>0. \end{align*} $$
$$ \begin{align*} \bigg| \int f d\mu -1 \bigg|>\epsilon>0. \end{align*} $$
It is a contradiction to equation (2.4). Therefore,
![]() $({1}/{N}) \sum _{n=0}^{N-1} f\circ T^n$
is converging uniformly to
$({1}/{N}) \sum _{n=0}^{N-1} f\circ T^n$
is converging uniformly to ![]() as N goes to infinity, in particular,
as N goes to infinity, in particular, ![]() .
.
Proof of Proposition 2.9
Let
![]() $\overline {\mathcal F}=\{\overline {f_1}, \ldots , \overline {f_p}\}$
and
$\overline {\mathcal F}=\{\overline {f_1}, \ldots , \overline {f_p}\}$
and
![]() $\mathcal G=\{g_1, \ldots , g_q\}$
be generating families of
$\mathcal G=\{g_1, \ldots , g_q\}$
be generating families of
![]() $\tilde {U}_T$
and
$\tilde {U}_T$
and
![]() $\underline {U}_T$
with
$\underline {U}_T$
with
![]() $p=\mathrm {Mult}(\tilde {U}_T)$
and
$p=\mathrm {Mult}(\tilde {U}_T)$
and
![]() $q=\mathrm {Mult}(\underline {U}_T)$
. For
$q=\mathrm {Mult}(\underline {U}_T)$
. For
![]() $1\le l\le p$
, take
$1\le l\le p$
, take
![]() $f_l\in C(X)$
to be a function such that
$f_l\in C(X)$
to be a function such that
![]() $\overline {f_l} = f_l \mod \overline {B_T(X)}$
, then let
$\overline {f_l} = f_l \mod \overline {B_T(X)}$
, then let
![]() $\mathcal F=\{f_1,\ldots , f_l\}$
. One easily checks that
$\mathcal F=\{f_1,\ldots , f_l\}$
. One easily checks that
![]() $\mathcal F\cup \mathcal G$
is a generating family of
$\mathcal F\cup \mathcal G$
is a generating family of
![]() $U_T$
. By Lemma 2.6, we may write
$U_T$
. By Lemma 2.6, we may write
![]() ${\mathcal M}_e(X, T)=\{\nu _1,\ldots ,\nu _p\}$
. As in the proof of Lemma 2.10, we may assume without loss of generality
${\mathcal M}_e(X, T)=\{\nu _1,\ldots ,\nu _p\}$
. As in the proof of Lemma 2.10, we may assume without loss of generality
![]() $\int f_i\, d\nu _j=\delta _{i,j}$
for any
$\int f_i\, d\nu _j=\delta _{i,j}$
for any
![]() $1\leq i,j\leq p$
. Let
$1\leq i,j\leq p$
. Let ![]() , and hence
, and hence
 $$ \begin{align*} \bigg(\int g^{\prime}_1\, d\nu_i \bigg)_{1\le i\le p}=(1,\ldots, 1). \end{align*} $$
$$ \begin{align*} \bigg(\int g^{\prime}_1\, d\nu_i \bigg)_{1\le i\le p}=(1,\ldots, 1). \end{align*} $$
By Remark 2.7, the family
![]() $\{ \overline {g^{\prime }_1}, \overline {f_j}: \ 1<j\le p \}$
is generating for
$\{ \overline {g^{\prime }_1}, \overline {f_j}: \ 1<j\le p \}$
is generating for
![]() $\tilde {U}_T$
. By Lemma 2.10, the constant functions, therefore also
$\tilde {U}_T$
. By Lemma 2.10, the constant functions, therefore also
![]() $g_1$
, belong to
$g_1$
, belong to
![]() $V_{ \{ g^{\prime }_1, f_j : \ 1<j\le p \} }$
. Then
$V_{ \{ g^{\prime }_1, f_j : \ 1<j\le p \} }$
. Then
![]() $V_{\{ g^{\prime }_1, f_j,g_i \ : \ 1<j\le p, \, 1<i\le q \} }=V_{\{ g^{\prime }_1, f_j,g_i \ : \ 1<j\le p, \, 1\le i\le q \} }$
and
$V_{\{ g^{\prime }_1, f_j,g_i \ : \ 1<j\le p, \, 1<i\le q \} }=V_{\{ g^{\prime }_1, f_j,g_i \ : \ 1<j\le p, \, 1\le i\le q \} }$
and
![]() $f_1\in V_{\{ g^{\prime }_1, f_j,g_i \ : \ 1<j\le p, \, 1\le i\le q \} }$
. Consequently, we get
$f_1\in V_{\{ g^{\prime }_1, f_j,g_i \ : \ 1<j\le p, \, 1\le i\le q \} }$
. Consequently, we get
We conclude that
![]() $\mathrm {Mult}(T)\leq p+q-1=\mathrm {Mult}(\tilde {U_T})+\mathrm {Mult}(\underline {U}_T)-1.$
$\mathrm {Mult}(T)\leq p+q-1=\mathrm {Mult}(\tilde {U_T})+\mathrm {Mult}(\underline {U}_T)-1.$
3 Affine embedding of
 $({\mathcal M}(X), T_*)$
in cubical shifts
$({\mathcal M}(X), T_*)$
in cubical shifts
For a topological system
![]() $(X,T)$
, we denote by
$(X,T)$
, we denote by
![]() $T_*$
the action induced by T on the compact set
$T_*$
the action induced by T on the compact set
![]() ${\mathcal M}(X)$
, that is,
${\mathcal M}(X)$
, that is,
![]() $T_*\mu (\cdot )=\mu (T^{-1}\cdot )$
for all
$T_*\mu (\cdot )=\mu (T^{-1}\cdot )$
for all
![]() $\mu \in {\mathcal M}(X)$
. Then
$\mu \in {\mathcal M}(X)$
. Then
![]() $({\mathcal M}(X), T_*)$
is also a topological system, which is called the induced system of
$({\mathcal M}(X), T_*)$
is also a topological system, which is called the induced system of
![]() $(X,T)$
.
$(X,T)$
.
For
![]() $d\in \mathbb N$
, we let
$d\in \mathbb N$
, we let
![]() $\sigma _d$
be the shift on the simplex
$\sigma _d$
be the shift on the simplex
![]() $([0,1]^d)^{\mathbb {Z}}$
. An embedding of
$([0,1]^d)^{\mathbb {Z}}$
. An embedding of
![]() $(X,T)$
in
$(X,T)$
in
![]() $([0,1]^d)^{\mathbb {Z}}$
is a continuous injective map
$([0,1]^d)^{\mathbb {Z}}$
is a continuous injective map
![]() $\phi :X\rightarrow ([0,1]^d)^{\mathbb {Z}}$
satisfying
$\phi :X\rightarrow ([0,1]^d)^{\mathbb {Z}}$
satisfying
![]() $\phi \circ T= \sigma _d \circ \phi $
. Existence of such an embedding is related to the mean dimension theory (we refer to [Reference CoornaertCoo15] for an introduction). Such an embedding implies that the mean dimension of
$\phi \circ T= \sigma _d \circ \phi $
. Existence of such an embedding is related to the mean dimension theory (we refer to [Reference CoornaertCoo15] for an introduction). Such an embedding implies that the mean dimension of
![]() $(X,T)$
is less than or equal to d. Moreover, the topological dimension (that is, Lebesgue covering dimension)
$(X,T)$
is less than or equal to d. Moreover, the topological dimension (that is, Lebesgue covering dimension)
![]() $d_n^T$
of the set of n-periodic points then also satisfy
$d_n^T$
of the set of n-periodic points then also satisfy
![]() $({d_n^T}/{n})\leq d$
. Conversely, it has been shown that minimal systems with mean dimension less than
$({d_n^T}/{n})\leq d$
. Conversely, it has been shown that minimal systems with mean dimension less than
![]() $d/2$
can be embedded in the cubical shift
$d/2$
can be embedded in the cubical shift
![]() $\sigma _d$
[Reference Gutman and TsukamotoGT20, Reference LindenstraussLin99].
$\sigma _d$
[Reference Gutman and TsukamotoGT20, Reference LindenstraussLin99].
In this section, we consider affine embedding of the induced system
![]() $({\mathcal M}(X), T_*)$
in cubical shift
$({\mathcal M}(X), T_*)$
in cubical shift
![]() $\sigma _d$
, that is, the embedding
$\sigma _d$
, that is, the embedding
![]() $\phi :{\mathcal M}(X)\rightarrow ([0,1]^d)^{\mathbb {Z}}$
is affine. In particular, we will relate the embedding dimension d to the multiplicity of
$\phi :{\mathcal M}(X)\rightarrow ([0,1]^d)^{\mathbb {Z}}$
is affine. In particular, we will relate the embedding dimension d to the multiplicity of
![]() $(X,T)$
.
$(X,T)$
.
3.1 Case of finite sets
We first deal with the case of a finite set X. Then T is just a permutation of X and
![]() ${\mathcal M}(X)$
is a finite dimensional simplex. We classify the possible affine embedding of
${\mathcal M}(X)$
is a finite dimensional simplex. We classify the possible affine embedding of
![]() $({\mathcal M}(X),T_*)$
in the following proposition.
$({\mathcal M}(X),T_*)$
in the following proposition.
Proposition 3.1. Suppose X is a finite set and T is a permutation of X. Let
![]() $\tau _1\cdots \tau _k$
be the decomposition of T into disjoint cycles
$\tau _1\cdots \tau _k$
be the decomposition of T into disjoint cycles
![]() $\tau _i$
of length
$\tau _i$
of length
![]() $r_i$
for
$r_i$
for
![]() $1\le i\le k$
.
$1\le i\le k$
.
-
(1) If there is a non-trivial common factor of
 $r_i$
for
$r_i$
for
 $1\le i\le k$
, then there is an affine embedding of
$1\le i\le k$
, then there is an affine embedding of
 $({\mathcal M}(X),T_*)$
in
$({\mathcal M}(X),T_*)$
in
 $( ([0,1]^k)^{{\mathbb {Z}}}, \sigma _k)$
. Such k is sharp.
$( ([0,1]^k)^{{\mathbb {Z}}}, \sigma _k)$
. Such k is sharp. -
(2) If there is no non-trivial common factor of
 $r_i$
for
$r_i$
for
 $1\le i\le k$
, then there is an affine embedding of
$1\le i\le k$
, then there is an affine embedding of
 $({\mathcal M}(X),T_*)$
in
$({\mathcal M}(X),T_*)$
in
 $( ([0,1]^{k-1})^{{\mathbb {Z}}}, \sigma _{k-1})$
. Such
$( ([0,1]^{k-1})^{{\mathbb {Z}}}, \sigma _{k-1})$
. Such
 $k-1$
is sharp.
$k-1$
is sharp.
Proof. For each
![]() $1\le i\le k$
, we fix a point
$1\le i\le k$
, we fix a point
![]() $e_i\in X$
in each cycle
$e_i\in X$
in each cycle
![]() $\tau _i$
, that is,
$\tau _i$
, that is,
![]() $\{T^je_i: 0\le j\le r_i \}=X$
. Notice that there are continuous maps
$\{T^je_i: 0\le j\le r_i \}=X$
. Notice that there are continuous maps
![]() $a_e:{\mathcal M}(X)\rightarrow [0,1]$
,
$a_e:{\mathcal M}(X)\rightarrow [0,1]$
,
![]() $e\in X$
, with
$e\in X$
, with ![]() satisfying
satisfying
![]() $\mu =\sum _{e\in X}a_e(\mu )\delta _e$
for all
$\mu =\sum _{e\in X}a_e(\mu )\delta _e$
for all
![]() $\mu \in {\mathcal M}(X)$
. (1) Assume there is a non-trivial common factor p of
$\mu \in {\mathcal M}(X)$
. (1) Assume there is a non-trivial common factor p of
![]() $r_i$
for
$r_i$
for
![]() $1\le i\le k$
. Then
$1\le i\le k$
. Then
where
![]() $\mathrm {Fix}(T_*^p)=\{\mu \in {\mathcal M}(X): \ T_*^p\mu =\mu \}$
. Since
$\mathrm {Fix}(T_*^p)=\{\mu \in {\mathcal M}(X): \ T_*^p\mu =\mu \}$
. Since
![]() $p>1$
and
$p>1$
and
![]() $\mathrm {dim}(\mathrm {Fix}(\sigma _{k-1}^p))=kp-p$
, the dynamical system
$\mathrm {dim}(\mathrm {Fix}(\sigma _{k-1}^p))=kp-p$
, the dynamical system
![]() $({\mathcal M}(X),T_*)$
cannot embed in
$({\mathcal M}(X),T_*)$
cannot embed in
![]() $( ([0,1]^{k-1})^{{\mathbb {Z}}}, \sigma _{k-1})$
.
$( ([0,1]^{k-1})^{{\mathbb {Z}}}, \sigma _{k-1})$
.
Now we construct the embedding of
![]() $({\mathcal M}(X),T_*)$
in
$({\mathcal M}(X),T_*)$
in
![]() $( ([0,1]^k)^{{\mathbb {Z}}}, \sigma _k)$
. We define first a dynamical embedding
$( ([0,1]^k)^{{\mathbb {Z}}}, \sigma _k)$
. We define first a dynamical embedding
![]() $\Psi $
of the set of extreme points in
$\Psi $
of the set of extreme points in
![]() ${\mathcal M}(X)$
, which is identified with X through the map
${\mathcal M}(X)$
, which is identified with X through the map
![]() $x\mapsto \delta _x$
, into
$x\mapsto \delta _x$
, into
![]() $([0,1]^k)^{\mathbb {Z}}$
by letting
$([0,1]^k)^{\mathbb {Z}}$
by letting
the other components
![]() $(\Psi (T^{l}e_i))_j$
,
$(\Psi (T^{l}e_i))_j$
,
![]() $j\neq i$
, being chosen to be equal to the
$j\neq i$
, being chosen to be equal to the
![]() $0^{\infty }$
sequence. Then we may extend
$0^{\infty }$
sequence. Then we may extend
![]() $\Psi $
affinely from the set of extreme points on
$\Psi $
affinely from the set of extreme points on
![]() ${\mathcal M}(X)$
by letting
${\mathcal M}(X)$
by letting
It is easy to check that
![]() $\Psi $
is injective, which deduces a dynamical embedding
$\Psi $
is injective, which deduces a dynamical embedding
![]() $({\mathcal M}(X),T_*)$
in
$({\mathcal M}(X),T_*)$
in
![]() $( ([0,1]^k)^{{\mathbb {Z}}}, \sigma _k)$
.
$( ([0,1]^k)^{{\mathbb {Z}}}, \sigma _k)$
.
(2) Assume there is no non-trivial common factor of
![]() $r_i$
for
$r_i$
for
![]() $1\le i\le k$
. We have that
$1\le i\le k$
. We have that
![]() $k-1$
numbers
$k-1$
numbers
![]() $q_{i}:=(r_k, r_i)$
,
$q_{i}:=(r_k, r_i)$
,
![]() $1\le i\le k-1$
are co-prime, where
$1\le i\le k-1$
are co-prime, where
![]() $(a,b)$
is the highest common factor of a and b. We define first a continuous map
$(a,b)$
is the highest common factor of a and b. We define first a continuous map
![]() $\Psi $
of the set of extreme points in
$\Psi $
of the set of extreme points in
![]() ${\mathcal M}(X)$
into
${\mathcal M}(X)$
into
![]() $([0,1]^{k-1})^{\mathbb {Z}}$
by letting
$([0,1]^{k-1})^{\mathbb {Z}}$
by letting
and
 $$ \begin{align*} &\text{for all } 1\le i\le k-1 , \text{ for all } l\in {\mathbb{Z}}, \quad (\Psi(T^{l}e_i))_{i}=\sigma^l ( (10^{r_i-1})^{\infty});\\ &\text{for all } j\not=i, \text{ for all } l\in {\mathbb{Z}}, \quad(\Psi(T^{l}e_i))_j=0^{\infty}.\end{align*} $$
$$ \begin{align*} &\text{for all } 1\le i\le k-1 , \text{ for all } l\in {\mathbb{Z}}, \quad (\Psi(T^{l}e_i))_{i}=\sigma^l ( (10^{r_i-1})^{\infty});\\ &\text{for all } j\not=i, \text{ for all } l\in {\mathbb{Z}}, \quad(\Psi(T^{l}e_i))_j=0^{\infty}.\end{align*} $$
Then we may extend
![]() $\Psi $
affinely from the set of extreme points on
$\Psi $
affinely from the set of extreme points on
![]() ${\mathcal M}(X)$
by letting
${\mathcal M}(X)$
by letting
It remains to show that
![]() $\Psi $
is injective. Let
$\Psi $
is injective. Let
![]() $\mu =\sum _{e\in X} b_e \delta _e$
and
$\mu =\sum _{e\in X} b_e \delta _e$
and
![]() $\mu '=\sum _{e\in X} b_e^{\prime } \delta _e$
. Suppose
$\mu '=\sum _{e\in X} b_e^{\prime } \delta _e$
. Suppose
Since
![]() $q_{i}:=(r_k, r_i)$
, then there are integers
$q_{i}:=(r_k, r_i)$
, then there are integers
![]() $s_i$
and
$s_i$
and
![]() $t_i$
such that
$t_i$
such that
![]() $ s_ir_i-t_ir_k=q_i. $
Let
$ s_ir_i-t_ir_k=q_i. $
Let
It implies that
Since
![]() $q_i, 1\le i\le k-1$
are co-prime, there are integers
$q_i, 1\le i\le k-1$
are co-prime, there are integers
![]() $w_i, 1\le i\le k-1$
such that
$w_i, 1\le i\le k-1$
such that
![]() $\sum _{i=1}^{k-1}w_iq_i=1$
. Since
$\sum _{i=1}^{k-1}w_iq_i=1$
. Since
 $$ \begin{align*} &(b_{e_k}-b_{T^{w_1q_1}e_k} )+(b_{T^{w_1q_1}e_k}-b_{T^{w_1q_1+w_2q_2}e_k} ) \\ &\quad+\cdots+(b_{T^{w_1q_1+w_2q_2+\cdots+w_{k-2}q_{k-2}}e_k}-b_{T^{w_1q_1+w_2q_2+\cdots+w_{k-1}q_{k-1}}e_k} )=b_{e_k}-b_{Te_k}, \end{align*} $$
$$ \begin{align*} &(b_{e_k}-b_{T^{w_1q_1}e_k} )+(b_{T^{w_1q_1}e_k}-b_{T^{w_1q_1+w_2q_2}e_k} ) \\ &\quad+\cdots+(b_{T^{w_1q_1+w_2q_2+\cdots+w_{k-2}q_{k-2}}e_k}-b_{T^{w_1q_1+w_2q_2+\cdots+w_{k-1}q_{k-1}}e_k} )=b_{e_k}-b_{Te_k}, \end{align*} $$
we have
Since
![]() $\sum _{e\in X}b_e=\sum _{e\in X}b_e^{\prime }=1$
, we conclude that
$\sum _{e\in X}b_e=\sum _{e\in X}b_e^{\prime }=1$
, we conclude that
![]() $b_{e_k}=b_{e_k^{\prime }}$
and consequently
$b_{e_k}=b_{e_k^{\prime }}$
and consequently
![]() $b_{e_i}=b_{e_i^{\prime }}$
by
$b_{e_i}=b_{e_i^{\prime }}$
by
![]() $b_{e_k}+b_{e_i}=b_{e_k}^{\prime }+b_{e_i}^{\prime }=c_{i,0}$
for
$b_{e_k}+b_{e_i}=b_{e_k}^{\prime }+b_{e_i}^{\prime }=c_{i,0}$
for
![]() $1\le i\le k-1$
. It means that
$1\le i\le k-1$
. It means that
![]() $\mu =\mu '$
and
$\mu =\mu '$
and
![]() $\Psi $
is injective.
$\Psi $
is injective.
Remark 3.2. For such a permutation T, we have
![]() $\mathrm {Mult}(T)=\sharp {\mathcal M}_e(X,T)=k$
, with k being the number of cycles in the decomposition of T.
$\mathrm {Mult}(T)=\sharp {\mathcal M}_e(X,T)=k$
, with k being the number of cycles in the decomposition of T.
3.1.1 General case
We consider now a general topological system and relate the dimension of the cubical shift in an affine embedding with the multiplicity of
![]() $(X,T)$
.
$(X,T)$
.
Theorem 3.3. Let
![]() $(X,T)$
be a topological system. If
$(X,T)$
be a topological system. If
![]() $\mathrm {Mult}(T)$
is equal to d, then there is an affine embedding of
$\mathrm {Mult}(T)$
is equal to d, then there is an affine embedding of
![]() $({\mathcal M}(X), T_*)$
in
$({\mathcal M}(X), T_*)$
in
![]() $(([0,1]^d)^{\mathbb {Z}},\sigma _d)$
. Conversely, if
$(([0,1]^d)^{\mathbb {Z}},\sigma _d)$
. Conversely, if
![]() $({\mathcal M}(X), T_*)$
embeds into
$({\mathcal M}(X), T_*)$
embeds into
![]() $(([0,1]^d)^{\mathbb {Z}},\sigma _d)$
, then:
$(([0,1]^d)^{\mathbb {Z}},\sigma _d)$
, then:
-
• either
 $\sharp {\mathcal M}_e(X,T)\leq d$
and
$\sharp {\mathcal M}_e(X,T)\leq d$
and
 $\mathrm {Mult}(T)\leq d$
;
$\mathrm {Mult}(T)\leq d$
; -
• or
 $\sharp {\mathcal M}_e(X,T)=d+1$
and
$\sharp {\mathcal M}_e(X,T)=d+1$
and
 $\mathrm {Mult}(T)=d+1$
.
$\mathrm {Mult}(T)=d+1$
.
Proof. First, notice that any affine equivariant map
![]() $\Psi :({\mathcal M}(X), T_*)\rightarrow (([0,1]^d)^{\mathbb {Z}},\sigma _d)$
is of the form
$\Psi :({\mathcal M}(X), T_*)\rightarrow (([0,1]^d)^{\mathbb {Z}},\sigma _d)$
is of the form
 $$ \begin{align*} \Psi_f:\mu\mapsto \bigg(\int f\circ T^k\, d\mu\bigg)_{k\in \mathbb{Z}} \end{align*} $$
$$ \begin{align*} \Psi_f:\mu\mapsto \bigg(\int f\circ T^k\, d\mu\bigg)_{k\in \mathbb{Z}} \end{align*} $$
for some continuous function
![]() $f=(f_1,\ldots ,f_d):X \rightarrow [0,1]^d$
.
$f=(f_1,\ldots ,f_d):X \rightarrow [0,1]^d$
.
Assume the topological multiplicity
![]() $\mathrm {Mult}(X,T)$
is equal to d, that is, there is a family
$\mathrm {Mult}(X,T)$
is equal to d, that is, there is a family
![]() $F=\{f_1,\ldots ,f_d\}$
of continuous functions such that
$F=\{f_1,\ldots ,f_d\}$
of continuous functions such that
![]() $V_F=C(X)$
. Let us show the associated map
$V_F=C(X)$
. Let us show the associated map
![]() $\Psi _f$
is injective. Let
$\Psi _f$
is injective. Let
![]() $\mu _1, \mu _2\in {\mathcal M}(X)$
with
$\mu _1, \mu _2\in {\mathcal M}(X)$
with
![]() $\Psi _f(\mu _1)=\Psi _f(\mu _1)$
, that is,
$\Psi _f(\mu _1)=\Psi _f(\mu _1)$
, that is,
![]() $\int f_i \circ T^k \,d\mu _1=\int f_i \circ T^k \, d\mu _1$
for any
$\int f_i \circ T^k \,d\mu _1=\int f_i \circ T^k \, d\mu _1$
for any
![]() $i=1, \ldots , d$
and any
$i=1, \ldots , d$
and any
![]() $k\in {\mathbb {Z}}$
. Then by density of
$k\in {\mathbb {Z}}$
. Then by density of
![]() $\mathrm {span}( f_i \circ T^k, \ i,\ k)$
in
$\mathrm {span}( f_i \circ T^k, \ i,\ k)$
in
![]() $C(X)$
, we have
$C(X)$
, we have
which implies
![]() $\mu _1=\mu _2$
. Therefore, we get the injectivity of
$\mu _1=\mu _2$
. Therefore, we get the injectivity of
![]() $\Psi _f$
.
$\Psi _f$
.
Conversely, assume
![]() $\Psi _f$
is injective for
$\Psi _f$
is injective for
![]() $f=(f_1,\ldots ,f_d):X \rightarrow [0,1]^d$
. Let
$f=(f_1,\ldots ,f_d):X \rightarrow [0,1]^d$
. Let ![]() . We claim that
. We claim that
![]() $V_F=C(X)$
. Then if
$V_F=C(X)$
. Then if
![]() $\sharp {\mathcal M}_e(X,T)\leq d$
, we get by injectivity of
$\sharp {\mathcal M}_e(X,T)\leq d$
, we get by injectivity of
![]() $\Psi _f$
that there exists
$\Psi _f$
that there exists
![]() $A\subset \{1,2, \ldots , d \}$
with
$A\subset \{1,2, \ldots , d \}$
with
![]() $\sharp A=\sharp {\mathcal M}_e(X,T)$
such that the matrix
$\sharp A=\sharp {\mathcal M}_e(X,T)$
such that the matrix
![]() $( \int f_i\, d\nu )_{i\in A, \nu \in {\mathcal M}_e(X,T)}$
is invertible. Then by Remark 2.7, the family
$( \int f_i\, d\nu )_{i\in A, \nu \in {\mathcal M}_e(X,T)}$
is invertible. Then by Remark 2.7, the family ![]() is generating for
is generating for
![]() $\tilde {U}_T$
and consequently
$\tilde {U}_T$
and consequently ![]() by Lemma 2.10. If
by Lemma 2.10. If
![]() $\sharp \mathcal M_e(X,T)= d+1$
, then we only get
$\sharp \mathcal M_e(X,T)= d+1$
, then we only get
![]() $\mathrm {Mult}(T)=d+1$
.
$\mathrm {Mult}(T)=d+1$
.
It remains to show our claim. Assume to the contrary that
![]() $V_F\not =C(X)$
. Then by the Riesz theorem, there is a signed finite measure
$V_F\not =C(X)$
. Then by the Riesz theorem, there is a signed finite measure
![]() $\mu $
vanishing on each function in F. Let
$\mu $
vanishing on each function in F. Let
![]() $\mu =\mu ^+-\mu ^-$
be the Jordan decomposition of
$\mu =\mu ^+-\mu ^-$
be the Jordan decomposition of
![]() $\mu $
(that is, the measures
$\mu $
(that is, the measures
![]() $\mu ^+$
and
$\mu ^+$
and
![]() $\mu ^-$
are two finite positive measures which are mutually singular). Evaluating on the constant function
$\mu ^-$
are two finite positive measures which are mutually singular). Evaluating on the constant function ![]() , we get
, we get
![]() $\mu ^+(X)=\mu ^-(X)$
. Then by rescaling, we may assume both
$\mu ^+(X)=\mu ^-(X)$
. Then by rescaling, we may assume both
![]() $\mu ^-$
and
$\mu ^-$
and
![]() $\mu ^+$
belong to
$\mu ^+$
belong to
![]() ${\mathcal M}(X)$
. Finally, we get
${\mathcal M}(X)$
. Finally, we get
![]() $\Psi _f(\mu ^+)=\Psi _f(\mu ^-)$
, and therefore
$\Psi _f(\mu ^+)=\Psi _f(\mu ^-)$
, and therefore
![]() $\mu ^+=\mu ^-$
by injectivity of
$\mu ^+=\mu ^-$
by injectivity of
![]() $\Psi _f$
contradicting the mutual singularity of
$\Psi _f$
contradicting the mutual singularity of
![]() $\mu ^+ $
and
$\mu ^+ $
and
![]() $\mu ^-$
.
$\mu ^-$
.
3.2 Affine embeddings and Lindenstrauss–Tsukamoto conjecture
Lindenstrauss and Tsukamoto [Reference Lindenstrauss and TsukamotoLT14] have conjectured that any topological system with mean dimension
![]() $\mathrm {mdim}(X,T)$
less than
$\mathrm {mdim}(X,T)$
less than
![]() $d/2$
and such that the dimension
$d/2$
and such that the dimension
![]() $d_n^T$
of the set of n-periodic points satisfies
$d_n^T$
of the set of n-periodic points satisfies
![]() $({d_n^T}/{n})< d/2$
for any
$({d_n^T}/{n})< d/2$
for any
![]() $n\in \mathbb N$
may be embedded in the shift over
$n\in \mathbb N$
may be embedded in the shift over
![]() $([0,1]^d)^{\mathbb {Z}}$
. As mentioned above, it is known for minimal systems. We consider here affine systems, that is, affine maps of a simplex. Such maps are never minimal, as they always admit at least one fixed point.
$([0,1]^d)^{\mathbb {Z}}$
. As mentioned above, it is known for minimal systems. We consider here affine systems, that is, affine maps of a simplex. Such maps are never minimal, as they always admit at least one fixed point.
The example below shows that the Lindenstrauss–Tsukamoto conjecture does not hold true in the affine category. Recall that an ergodic system
![]() $(X,f,{\mathcal B},\mu )$
has a countable Lebesgue spectrum when there is a countable family
$(X,f,{\mathcal B},\mu )$
has a countable Lebesgue spectrum when there is a countable family
![]() $(\psi _n)_{n\in \mathbb N}$
in
$(\psi _n)_{n\in \mathbb N}$
in
![]() $L^2_0(\mu )$
such that
$L^2_0(\mu )$
such that
![]() $\psi _n\circ f^k$
,
$\psi _n\circ f^k$
,
![]() $k\in {\mathbb {Z}}$
,
$k\in {\mathbb {Z}}$
,
![]() $n\in \mathbb N$
form a Hilbert basis of
$n\in \mathbb N$
form a Hilbert basis of
![]() $L^2_0(\mu )$
.
$L^2_0(\mu )$
.
Corollary 3.4. There is an affine system with a unique periodic (fixed) point and zero-topological entropy (in particular,
![]() $\mathrm{mdim}(T)=0$
and
$\mathrm{mdim}(T)=0$
and
![]() $d_n^T=0$
for all
$d_n^T=0$
for all
![]() $n\ge 1$
) which does not embed affinely in
$n\ge 1$
) which does not embed affinely in
![]() $(([0,1]^k)^{\mathbb {Z}},\sigma )$
for any
$(([0,1]^k)^{\mathbb {Z}},\sigma )$
for any
![]() $k\ge 1$
.
$k\ge 1$
.
Proof. There exists an ergodic measure-preserving system
![]() $(Y,\mathcal A,f,\mu )$
with zero entropy and countable Lebesgue spectrum [Reference Newton and ParryNP66, Reference ParasyukPar53] (in particular, totally ergodic, that is,
$(Y,\mathcal A,f,\mu )$
with zero entropy and countable Lebesgue spectrum [Reference Newton and ParryNP66, Reference ParasyukPar53] (in particular, totally ergodic, that is,
![]() $f^n$
is ergodic for any
$f^n$
is ergodic for any
![]() $n\in \mathbb {Z}$
). Then by the Jewett–Krieger theorem, there is a uniquely ergodic topological system
$n\in \mathbb {Z}$
). Then by the Jewett–Krieger theorem, there is a uniquely ergodic topological system
![]() $(X,T)$
with measure
$(X,T)$
with measure
![]() $\nu $
realizing such a measure-preserving system. All powers of T are uniquely ergodic as
$\nu $
realizing such a measure-preserving system. All powers of T are uniquely ergodic as
![]() $\mu $
was chosen totally ergodic. Moreover, the topological entropy of T, thus that of
$\mu $
was chosen totally ergodic. Moreover, the topological entropy of T, thus that of
![]() $T_*$
is zero by Glasner and Weiss [Reference Glasner and WeissGW95]. As the unique invariant measure
$T_*$
is zero by Glasner and Weiss [Reference Glasner and WeissGW95]. As the unique invariant measure
![]() $\nu $
has countable Lebesgue spectrum, the topological multiplicity of
$\nu $
has countable Lebesgue spectrum, the topological multiplicity of
![]() $(X,T)$
is infinite by Lemma 2.4. We conclude with Theorem 3.3.
$(X,T)$
is infinite by Lemma 2.4. We conclude with Theorem 3.3.
3.3 Application: zero topological entropy
A classical result in ergodic theory states that any ergodic system
![]() $(X,f,{\mathcal B},\mu )$
with positive entropy has a countable Lebesgue spectrum. In particular,
$(X,f,{\mathcal B},\mu )$
with positive entropy has a countable Lebesgue spectrum. In particular,
![]() $[h(\mu )>0]\Rightarrow [\mathrm { Mult}(\mu )=\infty ]$
. Then a proposition follows from the variational principle for the topological entropy.
$[h(\mu )>0]\Rightarrow [\mathrm { Mult}(\mu )=\infty ]$
. Then a proposition follows from the variational principle for the topological entropy.
Proposition 3.5. Any topological system
![]() $(X,T)$
with
$(X,T)$
with
![]() $\mathrm {Mult}(T)<\infty $
has zero topological entropy.
$\mathrm {Mult}(T)<\infty $
has zero topological entropy.
We may also give a purely topological proof of Proposition 3.5 based on mean dimension theory. More precisely, we use the main result of [Reference Burguet and ShiBS22], which states the following.
Theorem 3.6. [Reference Burguet and ShiBS22]
For any topological system
![]() $(X,T)$
with positive topological entropy, the induced system
$(X,T)$
with positive topological entropy, the induced system
![]() $({\mathcal M}(X), T_*)$
has infinite topological mean dimension. Therefore,
$({\mathcal M}(X), T_*)$
has infinite topological mean dimension. Therefore,
Topological proof of Proposition 3.5 .
Assume
![]() $\mathrm {Mult}(T)=d$
is finite. Then by Theorem 3.3, the induced system
$\mathrm {Mult}(T)=d$
is finite. Then by Theorem 3.3, the induced system
![]() $({\mathcal M}(X), T_*)$
embeds in the cubical shift
$({\mathcal M}(X), T_*)$
embeds in the cubical shift
![]() $(([0,1]^d)^{\mathbb {Z}},\sigma )$
. In particular, the mean dimension of
$(([0,1]^d)^{\mathbb {Z}},\sigma )$
. In particular, the mean dimension of
![]() $T_*$
is less than or equal to the mean dimension of the shift
$T_*$
is less than or equal to the mean dimension of the shift
![]() $(([0,1]^d)^{\mathbb {Z}},\sigma )$
, which is equal to d. By Theorem 3.6, it implies that T has zero topological entropy.
$(([0,1]^d)^{\mathbb {Z}},\sigma )$
, which is equal to d. By Theorem 3.6, it implies that T has zero topological entropy.
4 Baxter’s lemma in Banach spaces
In [Reference BaxterBax71], Baxter gave a useful criterion to show a simple spectrum of ergodic transformations. It may be extended more generally to bound the multiplicity of the spectrum (see, e.g., [Reference QueffélecQue10, Proposition 2.12]). We generalize this criterion for operators defined on a Banach space. It will be used in the next section to estimate the topological multiplicity in some examples.
Lemma 4.1. Let B be a separable Banach space and
![]() $\mathcal L(B)$
be the set of bounded linear operators on B. We consider an invertible isometry
$\mathcal L(B)$
be the set of bounded linear operators on B. We consider an invertible isometry
![]() $U\in \mathcal L(B)$
. If
$U\in \mathcal L(B)$
. If
![]() $(\mathcal {F}_n)_n$
is a sequence of finite subsets in H satisfying for all
$(\mathcal {F}_n)_n$
is a sequence of finite subsets in H satisfying for all
![]() $f\in B$
$f\in B$
then there exists a family
![]() $\mathcal {F}\subset B$
with
$\mathcal {F}\subset B$
with
![]() $\sharp \mathcal {F} \le \sup _n \sharp \mathcal {F}_n$
and
$\sharp \mathcal {F} \le \sup _n \sharp \mathcal {F}_n$
and
![]() $B=V_{\mathcal {F}}.$
$B=V_{\mathcal {F}}.$
Classical proofs of Baxter’s lemma strongly used the Hilbert structure. Here we use a Baire argument as in [Reference Pytheas FoggFog02, Lemma 5.2.10]. Note also that we do not require the sequence of vector spaces
![]() $(V_{\mathcal F_n})_n$
to be non-decreasing. Observe finally that it is enough to assume equation (4.1) for f in S, where S spans a dense subset of B.
$(V_{\mathcal F_n})_n$
to be non-decreasing. Observe finally that it is enough to assume equation (4.1) for f in S, where S spans a dense subset of B.
Proof. Let
![]() $m=\sup _n \sharp \mathcal {F}_n$
. If
$m=\sup _n \sharp \mathcal {F}_n$
. If
![]() $m=\infty $
, it is trivial. Assume
$m=\infty $
, it is trivial. Assume
![]() $m<\infty $
. By passing to a subsequence, we assume
$m<\infty $
. By passing to a subsequence, we assume
![]() $\sharp \mathcal {F}_n=m$
for all n. Let
$\sharp \mathcal {F}_n=m$
for all n. Let
![]() $B^{(m)}$
be the space of finite subsets of H whose cardinality is smaller than or equal to m. When endowed with the Hausdorff distance
$B^{(m)}$
be the space of finite subsets of H whose cardinality is smaller than or equal to m. When endowed with the Hausdorff distance
![]() $d_{\text {Hau}}$
, the space
$d_{\text {Hau}}$
, the space
![]() $B^{(m)}$
is a metric space, which is complete and separable. We assume the following claim, which we prove later on.
$B^{(m)}$
is a metric space, which is complete and separable. We assume the following claim, which we prove later on.
Claim 4.2. For any
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $\mathcal {F}\in B^{(m)}$
, the set
$\mathcal {F}\in B^{(m)}$
, the set
is open and dense.
Let
![]() $(g_q)_{q\in \mathbb N}$
be a countable dense family in B. Let
$(g_q)_{q\in \mathbb N}$
be a countable dense family in B. Let
![]() $\mathcal G_q$
be the finite family
$\mathcal G_q$
be the finite family
![]() $\{g_1,\ldots , g_q\}$
. For any
$\{g_1,\ldots , g_q\}$
. For any
![]() $p\in \mathbb N^*$
and any
$p\in \mathbb N^*$
and any
![]() $q\in \mathbb N $
, we consider the open and dense set
$q\in \mathbb N $
, we consider the open and dense set
According to Baire’s theorem, the intersection
![]() $\bigcap _{p,q}O_{p,q}$
is not empty. Clearly, any family
$\bigcap _{p,q}O_{p,q}$
is not empty. Clearly, any family
![]() $\mathcal F$
in the intersection satisfies
$\mathcal F$
in the intersection satisfies
![]() $V_{\mathcal F}=B$
. It remains to prove Claim 4.2.
$V_{\mathcal F}=B$
. It remains to prove Claim 4.2.
Proof of Claim 4.2
The set
![]() $O(\mathcal F,\epsilon )$
is open. We focus on the denseness property. Pick arbitrary
$O(\mathcal F,\epsilon )$
is open. We focus on the denseness property. Pick arbitrary
![]() $\delta>0$
and
$\delta>0$
and
![]() $\mathcal {H}\in B^{(m)}$
. We will show that there is
$\mathcal {H}\in B^{(m)}$
. We will show that there is
![]() ${\mathcal H}'\in O(\mathcal F,\epsilon )$
with
${\mathcal H}'\in O(\mathcal F,\epsilon )$
with
![]() $d_{\text {Hau}}({\mathcal H},{\mathcal H}')<\delta $
. As the elements of
$d_{\text {Hau}}({\mathcal H},{\mathcal H}')<\delta $
. As the elements of
![]() $B^{(m)}$
with cardinality m are dense in
$B^{(m)}$
with cardinality m are dense in
![]() $B^{(m)}$
, we can assume without loss of generality that
$B^{(m)}$
, we can assume without loss of generality that
![]() $\sharp {\mathcal H}=m$
. By assumptions on the sequence
$\sharp {\mathcal H}=m$
. By assumptions on the sequence
![]() $\mathcal F_n$
, there exists n such that
$\mathcal F_n$
, there exists n such that
We write
![]() $\mathcal {H}=\{h_1, h_2, \ldots , h_m \}$
and
$\mathcal {H}=\{h_1, h_2, \ldots , h_m \}$
and
![]() $\mathcal {F}_n=\{f_1, f_2, \ldots , f_m \}$
. By equation (4.3), there are polynomials
$\mathcal {F}_n=\{f_1, f_2, \ldots , f_m \}$
. By equation (4.3), there are polynomials
![]() $(P_{i,j})_{1\le i,j\le m}$
in
$(P_{i,j})_{1\le i,j\le m}$
in
![]() $\mathbb R[X]$
and a non-negative integer p such that
$\mathbb R[X]$
and a non-negative integer p such that
 $$ \begin{align} \text{ for all } i=1,\ldots,m, \quad \bigg\|h_i-\sum_{j=1}^m U^{-p} P_{i,j}(U)f_j\bigg\|<\delta. \end{align} $$
$$ \begin{align} \text{ for all } i=1,\ldots,m, \quad \bigg\|h_i-\sum_{j=1}^m U^{-p} P_{i,j}(U)f_j\bigg\|<\delta. \end{align} $$
Let
![]() $Q\in \mathbb R[X]$
be the polynomial given by the determinant of the matrix
$Q\in \mathbb R[X]$
be the polynomial given by the determinant of the matrix
![]() $M=(P_{i,j})_{1\le i,j\le m}\in M_m(\mathbb R[X])$
. The spectrum
$M=(P_{i,j})_{1\le i,j\le m}\in M_m(\mathbb R[X])$
. The spectrum
![]() $\mathrm {Sp}(U)$
of U is contained in the unit circle. In particular, for arbitrarily small
$\mathrm {Sp}(U)$
of U is contained in the unit circle. In particular, for arbitrarily small
![]() $\unicode{x3bb} \in \mathbb R$
, the polynomial
$\unicode{x3bb} \in \mathbb R$
, the polynomial
![]() $Q(\cdot +\unicode{x3bb} )$
does not vanish on
$Q(\cdot +\unicode{x3bb} )$
does not vanish on
![]() $\mathrm {Sp}(U)$
. Hence, by replacing
$\mathrm {Sp}(U)$
. Hence, by replacing
![]() $P_{i,j}$
by
$P_{i,j}$
by
![]() $P_{i,j}(\cdot +\unicode{x3bb} )$
, we may assume that Q does not vanish on the spectrum of U. Then
$P_{i,j}(\cdot +\unicode{x3bb} )$
, we may assume that Q does not vanish on the spectrum of U. Then
![]() $Q(U)=\prod _{\unicode{x3bb} , \, Q(\unicode{x3bb} )=0}(U-\unicode{x3bb} \mathrm {Id})$
is invertible and its inverse may be approximated by polynomials in U and
$Q(U)=\prod _{\unicode{x3bb} , \, Q(\unicode{x3bb} )=0}(U-\unicode{x3bb} \mathrm {Id})$
is invertible and its inverse may be approximated by polynomials in U and
![]() $U^{-1}$
, because for
$U^{-1}$
, because for
![]() $\unicode{x3bb} $
with
$\unicode{x3bb} $
with
![]() $Q(\unicode{x3bb} )=0$
, we have
$Q(\unicode{x3bb} )=0$
, we have
![]() $(U-\unicode{x3bb} \mathrm {Id})^{-1}{\kern-1pt}=-{\kern-1pt}\sum _{k\in \mathbb N}({U^k}/{\unicode{x3bb} ^{k+1}})$
for
$(U-\unicode{x3bb} \mathrm {Id})^{-1}{\kern-1pt}=-{\kern-1pt}\sum _{k\in \mathbb N}({U^k}/{\unicode{x3bb} ^{k+1}})$
for
![]() $|\unicode{x3bb} |>{\kern-1pt}1$
and
$|\unicode{x3bb} |>{\kern-1pt}1$
and
![]() $(U-\unicode{x3bb} \mathrm {Id})^{-1}{\kern-1pt}=-{\kern-1pt}\sum _{k\in \mathbb N}({U^{-(k+1)}}/{\unicode{x3bb} ^{k}})$
for
$(U-\unicode{x3bb} \mathrm {Id})^{-1}{\kern-1pt}=-{\kern-1pt}\sum _{k\in \mathbb N}({U^{-(k+1)}}/{\unicode{x3bb} ^{k}})$
for
![]() $|\unicode{x3bb} |<1$
(these sequences are normally convergent in
$|\unicode{x3bb} |<1$
(these sequences are normally convergent in
![]() $\mathcal L(B)$
as we assume
$\mathcal L(B)$
as we assume
![]() $\|U\|=\|U^{-1}\|=1$
). Let
$\|U\|=\|U^{-1}\|=1$
). Let
![]() ${\mathcal H}'=\{h^{\prime }_1, h^{\prime }_2, \ldots , h^{\prime }_m \}$
with
${\mathcal H}'=\{h^{\prime }_1, h^{\prime }_2, \ldots , h^{\prime }_m \}$
with
![]() $h^{\prime }_i=\sum _{j=1}^m U^{-p}P_{i,j}(U)f_j$
. We have
$h^{\prime }_i=\sum _{j=1}^m U^{-p}P_{i,j}(U)f_j$
. We have
 $$ \begin{align*}\mathcal F_n&= M(U)^{-1}U^p{\mathcal H}'\\ &=\mathrm{{}^{t}com} \, M(U)U^pQ(U)^{-1}{\mathcal H}'. \end{align*} $$
$$ \begin{align*}\mathcal F_n&= M(U)^{-1}U^p{\mathcal H}'\\ &=\mathrm{{}^{t}com} \, M(U)U^pQ(U)^{-1}{\mathcal H}'. \end{align*} $$
Then from the above observations, we get
In particular,
![]() $V_{\mathcal F_n}\subset V_{{\mathcal H}'}$
and it follows finally from equation (4.2) that
$V_{\mathcal F_n}\subset V_{{\mathcal H}'}$
and it follows finally from equation (4.2) that
![]() ${\mathcal H}'\in O(\mathcal F,\epsilon )$
, that is,
${\mathcal H}'\in O(\mathcal F,\epsilon )$
, that is,
This completes the proof as we have
![]() $d_{\text {Hau}}({\mathcal H},{\mathcal H}')<\delta $
by equation (4.4), where
$d_{\text {Hau}}({\mathcal H},{\mathcal H}')<\delta $
by equation (4.4), where
![]() ${\mathcal H}$
and
${\mathcal H}$
and
![]() $\delta $
have been chosen arbitrarily.
$\delta $
have been chosen arbitrarily.
5 Cantor systems with finite topological rank
Roughly speaking, an ergodic measure-preserving system is of finite rank r when it may be obtained by cutting and stacking with r Kakutani–Rohlin towers. For ergodic systems, Baxter’s lemma implies that the ergodic multiplicity is less than or equal to the rank. Topological rank has been defined and studied for minimal Cantor systems (see e.g. [Reference Donoso, Durand, Maass and PetiteDDMP21] and the references therein). For such systems, we show now with Lemma 4.1 that the same inequality holds for the topological quantities: the topological multiplicity is less than or equal to the topological rank.
First we recall the definition of topological rank. Let
![]() $(X,T)$
be a minimal Cantor system. A Kakutani–Rohlin partition of X is given by
$(X,T)$
be a minimal Cantor system. A Kakutani–Rohlin partition of X is given by
where
![]() $d, h(k), 1\le k\le d$
are positive integers and
$d, h(k), 1\le k\le d$
are positive integers and
![]() $B(k), 1\le k\le d$
are clopen subsets of X such that
$B(k), 1\le k\le d$
are clopen subsets of X such that
 $$ \begin{align*} \bigcup_{k=1}^{d} T^{-h(k)}B(k)=\bigcup_{k=1}^{d} B(k). \end{align*} $$
$$ \begin{align*} \bigcup_{k=1}^{d} T^{-h(k)}B(k)=\bigcup_{k=1}^{d} B(k). \end{align*} $$
The base of
![]() $\mathcal {T}$
is the set
$\mathcal {T}$
is the set
![]() $B(\mathcal {T})=\bigcup _{k=1}^{d} B(k)$
. A sequence of Kakutani–Rohlin partitions
$B(\mathcal {T})=\bigcup _{k=1}^{d} B(k)$
. A sequence of Kakutani–Rohlin partitions
is nested if:
-
(1)
 $\mathcal {T}_0$
is the trivial partition, that is,
$\mathcal {T}_0$
is the trivial partition, that is,
 $d_0=1, h_0=1$
and
$d_0=1, h_0=1$
and
 $B_0(1)=X$
;
$B_0(1)=X$
; -
(2)
 $B(\mathcal {T}_{n+1})\subset B(\mathcal {T}_n)$
;
$B(\mathcal {T}_{n+1})\subset B(\mathcal {T}_n)$
; -
(3)
 $\mathcal {T}_{n+1}\succ \mathcal {T}_n$
;
$\mathcal {T}_{n+1}\succ \mathcal {T}_n$
; -
(4)
 $\sharp (\bigcap _{n\ge 0} B(\mathcal {T}_n))=1$
;
$\sharp (\bigcap _{n\ge 0} B(\mathcal {T}_n))=1$
; -
(5)
 $\bigcup _{n\ge 1} \mathcal {T}_n$
spans the topology of X.
$\bigcup _{n\ge 1} \mathcal {T}_n$
spans the topology of X.
Moreover, it is primitive if for all
![]() $n\ge 1$
, there exists
$n\ge 1$
, there exists
![]() $N> n$
such that for all
$N> n$
such that for all
![]() $1 \le k \le d_N$
and for each
$1 \le k \le d_N$
and for each
![]() $x\in T^{-(hN (k)-1)}B_N(k)$
,
$x\in T^{-(hN (k)-1)}B_N(k)$
,
Following [Reference Donoso, Durand, Maass and PetiteDDMP21], a minimal Cantor system is of topological rank d if it admits a primitive sequence of nested Kakutani–Rohlin partitions with
![]() $d_n\le d$
for all
$d_n\le d$
for all
![]() $n\in \mathbb {N}$
.
$n\in \mathbb {N}$
.
Theorem 5.1. Let
![]() $(X,T)$
be a minimal Cantor system with topological rank d. Then
$(X,T)$
be a minimal Cantor system with topological rank d. Then
![]() $\mathrm {Mult}(X,T)\le d$
.
$\mathrm {Mult}(X,T)\le d$
.
Proof. Let
![]() $(\mathcal {T}_n)_{n\in \mathbb {N}}$
be the primitive sequence of nested Kakutani–Rohlin partitions with
$(\mathcal {T}_n)_{n\in \mathbb {N}}$
be the primitive sequence of nested Kakutani–Rohlin partitions with
![]() $d_n\le d$
for all
$d_n\le d$
for all
![]() $n\in \mathbb {N}$
. Let
$n\in \mathbb {N}$
. Let
Since
![]() $\bigcup _{n\ge 1} \mathcal {T}_n$
spans the topology of X, we have
$\bigcup _{n\ge 1} \mathcal {T}_n$
spans the topology of X, we have
It follows from Lemma 4.1 and
![]() $d_n\le d$
for all
$d_n\le d$
for all
![]() $n\in \mathbb {N}$
that
$n\in \mathbb {N}$
that
![]() $\mathrm {Mult}(X,T)\le d$
.
$\mathrm {Mult}(X,T)\le d$
.
Remark 5.2. It was shown in [Reference Donoso, Durand, Maass and PetiteDDMP21] that the Thue–Morse subshift has topological rank
![]() $3$
. By Theorem 5.1, the Thue–Morse subshift has therefore topological multiplicity at most
$3$
. By Theorem 5.1, the Thue–Morse subshift has therefore topological multiplicity at most
![]() $3$
. However, we will prove in Proposition 6.7 that the Thue–Morse subshift has simple topological multiplicity.
$3$
. However, we will prove in Proposition 6.7 that the Thue–Morse subshift has simple topological multiplicity.
Examples of ergodic systems with rank r and multiplicity m have been built for any
![]() $1\leq m\leq r$
in [Reference Kwiatkowski and LacroixKL97]. We then propose the following question.
$1\leq m\leq r$
in [Reference Kwiatkowski and LacroixKL97]. We then propose the following question.
Question 5.3. Can one build for any
![]() $1\leq m\leq r$
a minimal Cantor system with topological multiplicity m and topological rank r?
$1\leq m\leq r$
a minimal Cantor system with topological multiplicity m and topological rank r?
6 Examples of finite topological multiplicity
An invertible dynamical system is called topological simple or has a simple topological spectrum if
![]() $\mathrm {Mult}(T)=1$
.
$\mathrm {Mult}(T)=1$
.
6.0.1 Minimal rotation on compact groups
Let G be a compact abelian group. Denote by
![]() $\hat G $
the dual group of G and by
$\hat G $
the dual group of G and by
![]() $\unicode{x3bb} $
the Haar measure on G. For
$\unicode{x3bb} $
the Haar measure on G. For
![]() $f\in C(G)$
, we write
$f\in C(G)$
, we write
![]() $\hat {f}$
the Fourier transformation of f.
$\hat {f}$
the Fourier transformation of f.
Proposition 6.1. Any minimal translation
![]() $\tau $
on a compact abelian group G is topologically simple.
$\tau $
on a compact abelian group G is topologically simple.
Proof. We claim that any
![]() $f\in C(G)$
with
$f\in C(G)$
with
![]() $\hat f(\chi )\neq 0$
for all
$\hat f(\chi )\neq 0$
for all
![]() $\chi \in \hat G$
is cyclic, that is, the vector space spanned by
$\chi \in \hat G$
is cyclic, that is, the vector space spanned by
![]() $f\circ \tau ^k$
,
$f\circ \tau ^k$
,
![]() $k\in \mathbb N$
is dense in
$k\in \mathbb N$
is dense in
![]() $C(X)$
. As characters of a compact abelian group separate points, it is enough to show by the Stone–Weierstrass theorem that any character belongs to the complex vector space spanned by
$C(X)$
. As characters of a compact abelian group separate points, it is enough to show by the Stone–Weierstrass theorem that any character belongs to the complex vector space spanned by
![]() $f\circ \tau ^k$
,
$f\circ \tau ^k$
,
![]() $k\in \mathbb N$
. However, for all
$k\in \mathbb N$
. However, for all
![]() $\chi \in \hat G $
, we have
$\chi \in \hat G $
, we have
Then with the function f being uniformly continuous, there are functions of the form
![]() $\sum _k f(\cdot -y_k)\chi (y_k)$
arbitrarily close to
$\sum _k f(\cdot -y_k)\chi (y_k)$
arbitrarily close to
![]() $\hat f(\chi ) \chi $
for the supremum norm. By minimality of
$\hat f(\chi ) \chi $
for the supremum norm. By minimality of
![]() $\tau $
, there are integers
$\tau $
, there are integers
![]() $l_k\in \mathbb N$
such that
$l_k\in \mathbb N$
such that
![]() $f\circ \tau ^{l_k}$
and
$f\circ \tau ^{l_k}$
and
![]() $f(\cdot -y_k)$
are arbitrarily closed. It concludes the proof.
$f(\cdot -y_k)$
are arbitrarily closed. It concludes the proof.
6.0.2 Sturmian subshift
A word
![]() $u \in \{0, 1\}^{{\mathbb {Z}}}$
is called Sturmian if it is recurrent under the shift
$u \in \{0, 1\}^{{\mathbb {Z}}}$
is called Sturmian if it is recurrent under the shift
![]() $\sigma $
, and the number of n-words in u equals
$\sigma $
, and the number of n-words in u equals
![]() $ n + 1$
for each
$ n + 1$
for each
![]() $n \geq 1$
. Take the shift-orbit closure
$n \geq 1$
. Take the shift-orbit closure
![]() $X_u =\overline { O_{\sigma }(u)}$
. The corresponding subshift
$X_u =\overline { O_{\sigma }(u)}$
. The corresponding subshift
![]() $(X_u,\sigma )$
is called a Sturmian subshift. Sturmian sequences are symbolic representation of circle irrational rotations.
$(X_u,\sigma )$
is called a Sturmian subshift. Sturmian sequences are symbolic representation of circle irrational rotations.
We first recall some standard notation in symbolic dynamics. For a subset Y of
![]() $\mathcal A^{{\mathbb {Z}}}$
with
$\mathcal A^{{\mathbb {Z}}}$
with
![]() $\mathcal A$
being a finite alphabet, we let
$\mathcal A$
being a finite alphabet, we let
![]() $\mathcal L_n(Y)$
be the number of n-words appearing in the sequences of Y. Then for
$\mathcal L_n(Y)$
be the number of n-words appearing in the sequences of Y. Then for
![]() $w\in \mathcal L_n(Y)$
, we let
$w\in \mathcal L_n(Y)$
, we let
![]() $[w]$
be the associated cylinder defined as
$[w]$
be the associated cylinder defined as
![]() $[w]:=\{(x_n)_{n\in \mathbb {Z}}\in Y: \ x_0\cdots x_{n-1}=w\}.$
The indicator function of a subset E of X will be denoted by
$[w]:=\{(x_n)_{n\in \mathbb {Z}}\in Y: \ x_0\cdots x_{n-1}=w\}.$
The indicator function of a subset E of X will be denoted by
![]() $\chi _E$
.
$\chi _E$
.
Proposition 6.2. Any Sturmian subshift has simple topological spectrum.
Proof. Let u be a Sturmian sequence. Let
It follows that
Notice
![]() $\dim (F_n)=\sharp \mathcal {L}_n(u) =n+1$
. We let
$\dim (F_n)=\sharp \mathcal {L}_n(u) =n+1$
. We let
![]() $f:X_u\rightarrow \mathbb R$
be the continuous function defined as
$f:X_u\rightarrow \mathbb R$
be the continuous function defined as
![]() $f:x=(x_n)_n\mapsto (-1)^{x_0}$
. Let
$f:x=(x_n)_n\mapsto (-1)^{x_0}$
. Let
Clearly,
![]() $G_n\subset F_n$
. To prove that
$G_n\subset F_n$
. To prove that
![]() $(X_u, \sigma )$
has simple topological spectrum, it is sufficient to show
$(X_u, \sigma )$
has simple topological spectrum, it is sufficient to show
![]() $\dim (G_n)=n+1$
. Thus, it is enough to show the functions
$\dim (G_n)=n+1$
. Thus, it is enough to show the functions ![]() are linearly independent. If not, for some n, there exists a non-zero vector
are linearly independent. If not, for some n, there exists a non-zero vector
![]() $(a_0, a_1, \ldots , a_n)$
such that
$(a_0, a_1, \ldots , a_n)$
such that
Since
![]() $\sharp \mathcal L_{n-1}(u)> \sharp \mathcal L_{n-2}(u)$
, we can find distinct
$\sharp \mathcal L_{n-1}(u)> \sharp \mathcal L_{n-2}(u)$
, we can find distinct
![]() $x, x'\in X_u$
such that
$x, x'\in X_u$
such that
![]() $x|_0^{n-2}=x'|_0^{n-2}$
but
$x|_0^{n-2}=x'|_0^{n-2}$
but
![]() $x_{n-1}\not =x^{\prime }_{n-1}$
. It follows that
$x_{n-1}\not =x^{\prime }_{n-1}$
. It follows that
![]() $a_{n-1}=0$
. Since for each
$a_{n-1}=0$
. Since for each
![]() $0\le k\le n-2$
we can always find
$0\le k\le n-2$
we can always find
![]() $y, y'$
such that
$y, y'$
such that
![]() $y|_0^{k-1}=y'|_0^{k-1}$
but
$y|_0^{k-1}=y'|_0^{k-1}$
but
![]() $y_{k}\not =y^{\prime }_{k}$
, we obtain that
$y_{k}\not =y^{\prime }_{k}$
, we obtain that
![]() $a_{n-2}=a_{n-3}=\cdots =a_{0}=0$
. Finally, we get
$a_{n-2}=a_{n-3}=\cdots =a_{0}=0$
. Finally, we get
![]() $a_n=0$
. This is a contradiction. Therefore, we conclude that
$a_n=0$
. This is a contradiction. Therefore, we conclude that
![]() $\dim (G_n)=n+1$
, then
$\dim (G_n)=n+1$
, then
![]() $F_n=G_n$
. Then by Lemma 4.1,
$F_n=G_n$
. Then by Lemma 4.1,
![]() $(X_u, \sigma )$
has simple topological spectrum.
$(X_u, \sigma )$
has simple topological spectrum.
6.0.3 Homeomorphism of the interval
Estimating the multiplicity of non-zero dimensional systems is difficult in general. Below we focus on homeomorphisms of the interval (see [Reference JavaheriJav19] for related results on the circle). We use the following result due to Atzmon and Olevskii [Reference Atzmon and OlevskiĭAO96]. We denote by
![]() $C_0(\mathbb R)$
the set of continuous map on
$C_0(\mathbb R)$
the set of continuous map on
![]() $\mathbb R$
with zero limits in
$\mathbb R$
with zero limits in
![]() $\pm \infty $
. For
$\pm \infty $
. For
![]() $f\in C_0(\mathbb R)$
and
$f\in C_0(\mathbb R)$
and
![]() $n\in {\mathbb {Z}}$
, we let
$n\in {\mathbb {Z}}$
, we let
![]() $f_n=f(\cdot +n)$
be the translation of f by n.
$f_n=f(\cdot +n)$
be the translation of f by n.
Theorem 6.3. [Reference Atzmon and OlevskiĭAO96]
There exists
![]() $g\in C_0(\mathbb R)$
such that the vector space spanned by
$g\in C_0(\mathbb R)$
such that the vector space spanned by
![]() $g_n$
,
$g_n$
,
![]() $n\in \mathbb N$
is dense in
$n\in \mathbb N$
is dense in
![]() $ C_0(\mathbb R)$
.
$ C_0(\mathbb R)$
.
In particular, the operator
![]() $V: C_0(\mathbb R)\circlearrowleft $
,
$V: C_0(\mathbb R)\circlearrowleft $
,
![]() $f\mapsto f(\cdot +1) $
, is cyclic. A Borel set S of
$f\mapsto f(\cdot +1) $
, is cyclic. A Borel set S of
![]() $\mathbb R$
is called a set of uniqueness if the sets
$\mathbb R$
is called a set of uniqueness if the sets
![]() $S_n:=(S+2\pi n)\cap [-\pi ,\pi ]$
,
$S_n:=(S+2\pi n)\cap [-\pi ,\pi ]$
,
![]() $n\in {\mathbb {Z}}$
satisfy the following properties:
$n\in {\mathbb {Z}}$
satisfy the following properties:
-
(1)
 $S_n$
,
$S_n$
,
 $n\in {\mathbb {Z}}$
, are pairwise disjoint;
$n\in {\mathbb {Z}}$
, are pairwise disjoint; -
(2)
 $\mathrm {Leb}(S_n\cap U)>0$
for any
$\mathrm {Leb}(S_n\cap U)>0$
for any
 $n\in \mathbb {Z}$
and any open set U of
$n\in \mathbb {Z}$
and any open set U of
 $[-\pi , \pi ]$
;
$[-\pi , \pi ]$
; -
(3)
 $\mathrm {Leb}(S)<\infty $
,
$\mathrm {Leb}(S)<\infty $
,
where
![]() $\mathrm {Leb}$
denotes the Lebesgue measure on
$\mathrm {Leb}$
denotes the Lebesgue measure on
![]() $\mathbb {R}$
.
$\mathbb {R}$
.
Atzmon and Olevskii proved for any set of uniqueness S (such sets exist!), the conclusion of Theorem 6.3 holds true with g being the the Fourier transform of the indicator function of S. Let us just remark that if S is a set of uniqueness, then
are k disjoints sets of uniqueness. Let
![]() $C_0(\mathbb R;\mathbb C)$
be the set of continuous maps on
$C_0(\mathbb R;\mathbb C)$
be the set of continuous maps on
![]() $\mathbb C$
with zero limits in infinity.
$\mathbb C$
with zero limits in infinity.
Lemma 6.4. The operator
![]() $V: C_0(\mathbb R;\mathbb C)^{k}\circlearrowleft $
,
$V: C_0(\mathbb R;\mathbb C)^{k}\circlearrowleft $
,
![]() $(f_i)_{1\leq i\leq k}\mapsto (f_i(\cdot +1))_{1\leq i\leq k}$
is cyclic. In particular, the operator
$(f_i)_{1\leq i\leq k}\mapsto (f_i(\cdot +1))_{1\leq i\leq k}$
is cyclic. In particular, the operator
![]() $U: C_0(\mathbb R)^{k}\circlearrowleft $
,
$U: C_0(\mathbb R)^{k}\circlearrowleft $
,
![]() $(f_i)_{1\leq i\leq k}\mapsto (f_i(\cdot +1))_{1\leq i\leq k}$
is cyclic.
$(f_i)_{1\leq i\leq k}\mapsto (f_i(\cdot +1))_{1\leq i\leq k}$
is cyclic.
Proof. Let S,
![]() $S^l$
,
$S^l$
,
![]() $1\leq l\leq k$
, be sets of uniqueness as above. By following [Reference Atzmon and OlevskiĭAO96], we show that the vector space generated by the translates of
$1\leq l\leq k$
, be sets of uniqueness as above. By following [Reference Atzmon and OlevskiĭAO96], we show that the vector space generated by the translates of
![]() $g:=(\widehat {\chi _{S^l}})_{1\leq l\leq k}$
is dense in
$g:=(\widehat {\chi _{S^l}})_{1\leq l\leq k}$
is dense in
![]() $C_0(\mathbb R;\mathbb C)^{k}$
with
$C_0(\mathbb R;\mathbb C)^{k}$
with
![]() $\widehat {\chi _{S^l}} $
the Fourier transform of the indicator function
$\widehat {\chi _{S^l}} $
the Fourier transform of the indicator function
![]() $\chi _{S^l}$
of
$\chi _{S^l}$
of
![]() $S^l$
. It follows that the translates of
$S^l$
. It follows that the translates of
![]() $Re(g)$
are dense in
$Re(g)$
are dense in
![]() $C_0(\mathbb R)^{k}$
. Let
$C_0(\mathbb R)^{k}$
. Let
![]() $\mu =(\mu _l)_{1\leq l\leq k}$
be a complex bounded measure with
$\mu =(\mu _l)_{1\leq l\leq k}$
be a complex bounded measure with
 $$ \begin{align*} \langle V^n(g), \mu \rangle=\sum_{1\leq l\leq k} \int (\widehat{\chi_{S^l}})_n\, d\mu_l=0 \end{align*} $$
$$ \begin{align*} \langle V^n(g), \mu \rangle=\sum_{1\leq l\leq k} \int (\widehat{\chi_{S^l}})_n\, d\mu_l=0 \end{align*} $$
for all
![]() $n\in {\mathbb {Z}}$
. It is enough to prove
$n\in {\mathbb {Z}}$
. It is enough to prove
![]() $\mu _l=0$
for all
$\mu _l=0$
for all
![]() $1\leq l\leq k$
. By the Plancherel–Parseval formula, we have
$1\leq l\leq k$
. By the Plancherel–Parseval formula, we have
Therefore, we have
 $$ \begin{align*}\sum_{1\leq l\leq k} \int \chi_{S^l}(t) \hat{\mu_l}(t)e^{-int}\, dt=0\end{align*} $$
$$ \begin{align*}\sum_{1\leq l\leq k} \int \chi_{S^l}(t) \hat{\mu_l}(t)e^{-int}\, dt=0\end{align*} $$
for all n. However, this term is just the nth coefficient of the function of
![]() $L^1([-\pi ,\pi ])$
given by
$L^1([-\pi ,\pi ])$
given by
![]() $\sum _{m\in {\mathbb {Z}}}(\sum _{1\leq l\leq k} \chi _{S^l}\hat \mu _l)(\cdot +2\pi m) $
, which should therefore be
$\sum _{m\in {\mathbb {Z}}}(\sum _{1\leq l\leq k} \chi _{S^l}\hat \mu _l)(\cdot +2\pi m) $
, which should therefore be
![]() $0$
. As the sets
$0$
. As the sets
![]() $(S^l+2\pi m)\cap [- \pi ,\pi ], m\in \mathbb {Z},$
are pairwise disjoint, each term of the previous sum should be zero; that is,
$(S^l+2\pi m)\cap [- \pi ,\pi ], m\in \mathbb {Z},$
are pairwise disjoint, each term of the previous sum should be zero; that is,
![]() $(\chi _{S^l}\hat \mu _l)(x +2\pi k)=0$
for all
$(\chi _{S^l}\hat \mu _l)(x +2\pi k)=0$
for all
![]() $m,l$
and for Lebesgue almost every
$m,l$
and for Lebesgue almost every
![]() $x\in [-\pi , \pi ]$
. By Property (2) in the definition of a set of uniqueness, we conclude
$x\in [-\pi , \pi ]$
. By Property (2) in the definition of a set of uniqueness, we conclude
![]() $\widehat {\mu _l}=0$
. Therefore,
$\widehat {\mu _l}=0$
. Therefore,
![]() $\mu _l=0$
for each
$\mu _l=0$
for each
![]() $1\leq l\leq k$
and consequently the translates of g are dense in
$1\leq l\leq k$
and consequently the translates of g are dense in
![]() $C_0(\mathbb R;\mathbb C)^{k}$
.
$C_0(\mathbb R;\mathbb C)^{k}$
.
Proposition 6.5. Let
![]() $f:[0,1]\circlearrowleft $
be a homeomorphism of the interval. Then
$f:[0,1]\circlearrowleft $
be a homeomorphism of the interval. Then
Proof. We first deal with the case of an increasing homeomorphism. The ergodic measures of f are the Dirac measures at these fixed points. Notice that f has at least two fixed points,
![]() $0$
and
$0$
and
![]() $1$
. If it has infinitely many fixed points, then
$1$
. If it has infinitely many fixed points, then
![]() $\mathrm {Mult}(U_f)\ge \sharp {\mathcal M}_e([0,1],f)=\infty $
. Now assume it has finitely many fixed points. Let
$\mathrm {Mult}(U_f)\ge \sharp {\mathcal M}_e([0,1],f)=\infty $
. Now assume it has finitely many fixed points. Let
![]() $2\le k+1<+\infty $
be the number of fixed points. Since
$2\le k+1<+\infty $
be the number of fixed points. Since
![]() $\varphi (x)-\varphi \circ f (x)=0$
for any continuous function
$\varphi (x)-\varphi \circ f (x)=0$
for any continuous function
![]() $\varphi \in C(X)$
and any fixed point x, the space
$\varphi \in C(X)$
and any fixed point x, the space
![]() $\overline {B_f([0,1])}$
is the set of real continuous maps on the interval which vanishes at the fixed points. It follows that the operator
$\overline {B_f([0,1])}$
is the set of real continuous maps on the interval which vanishes at the fixed points. It follows that the operator
![]() $\underline {U}_f$
is spectrally conjugate to
$\underline {U}_f$
is spectrally conjugate to
![]() $V: C_0(\mathbb R)^{k}\circlearrowleft $
,
$V: C_0(\mathbb R)^{k}\circlearrowleft $
,
![]() $(f_i)_{1\leq i\leq k}\mapsto (f_i(\cdot +1))_{1\leq i\leq k}$
. By Lemma 6.4, we have
$(f_i)_{1\leq i\leq k}\mapsto (f_i(\cdot +1))_{1\leq i\leq k}$
. By Lemma 6.4, we have
![]() $\mathrm { Mult}(\underline {U_f})=1$
. It follows then from Propositions 2.9 and 2.6 that
$\mathrm { Mult}(\underline {U_f})=1$
. It follows then from Propositions 2.9 and 2.6 that
It remains to consider the case of a decreasing homeomorphism f. Let
![]() $0<a<1$
be the unique fixed point of f. Then
$0<a<1$
be the unique fixed point of f. Then
![]() $f^{2}:[0,a]\circlearrowleft $
is an increasing homeomorphism. Let
$f^{2}:[0,a]\circlearrowleft $
is an increasing homeomorphism. Let
![]() $0=x_1<x_2<\cdots <x_k=a$
be the fixed points of
$0=x_1<x_2<\cdots <x_k=a$
be the fixed points of
![]() $f^{2}|_{[0,a]}$
. Then the ergodic measures of f are the atomic periodic measures
$f^{2}|_{[0,a]}$
. Then the ergodic measures of f are the atomic periodic measures
![]() $\delta _a$
and
$\delta _a$
and
![]() $\tfrac 12(\delta _{x_i}+\delta _{f(x_i)})$
for
$\tfrac 12(\delta _{x_i}+\delta _{f(x_i)})$
for
![]() $i=1, \ldots , k-1$
. In particular, we have
$i=1, \ldots , k-1$
. In particular, we have
![]() $k=\sharp {\mathcal M}_e([0,1],f)$
. From the previous case, there is a generating family
$k=\sharp {\mathcal M}_e([0,1],f)$
. From the previous case, there is a generating family
![]() $\mathcal G=\{g_1, \ldots , g_k\}$
for
$\mathcal G=\{g_1, \ldots , g_k\}$
for
![]() $f^{2}:[0,a]\circlearrowleft $
. Let
$f^{2}:[0,a]\circlearrowleft $
. Let
![]() $h\in C([0,1])$
. For any
$h\in C([0,1])$
. For any
![]() $\epsilon>0$
, there are
$\epsilon>0$
, there are
![]() $N\in \mathbb N$
,
$N\in \mathbb N$
,
![]() $a_{l,n}$
and
$a_{l,n}$
and
![]() $b_{l,n}$
, for
$b_{l,n}$
, for
![]() $l=1,\ldots , k $
and
$l=1,\ldots , k $
and
![]() $|n|\leq N$
, (depending on
$|n|\leq N$
, (depending on
![]() $\epsilon $
), such that
$\epsilon $
), such that
 $$ \begin{align} \bigg\|h-\sum_{l,n}a_{l,n}g_l\circ f^{2n}\bigg\|_{{[0,a]},\infty}&<\epsilon \end{align} $$
$$ \begin{align} \bigg\|h-\sum_{l,n}a_{l,n}g_l\circ f^{2n}\bigg\|_{{[0,a]},\infty}&<\epsilon \end{align} $$
and
 $$ \begin{align} \bigg\|h\circ f^{-1} -\sum_{l,n}b_{l,n}g_l\circ f^{2n}-h(a)\bigg\|_{{[0,a]},\infty}&<\epsilon, \end{align} $$
$$ \begin{align} \bigg\|h\circ f^{-1} -\sum_{l,n}b_{l,n}g_l\circ f^{2n}-h(a)\bigg\|_{{[0,a]},\infty}&<\epsilon, \end{align} $$
where
![]() $\|g\|_{{[0,a]},\infty }=\sup _{x\in [0,a]} |g(x)|$
. We consider the extension
$\|g\|_{{[0,a]},\infty }=\sup _{x\in [0,a]} |g(x)|$
. We consider the extension
![]() $\tilde {g_l}$
of
$\tilde {g_l}$
of
![]() $g_l$
to
$g_l$
to
![]() $[0,1]$
with
$[0,1]$
with
![]() $\tilde {g_l}=g_l(a)$
on
$\tilde {g_l}=g_l(a)$
on
![]() $[a,1]$
. We check now that
$[a,1]$
. We check now that
![]() $\tilde {\mathcal G}=\{\tilde g_1, \ldots , \tilde g_k\}$
is generating for f. It follows from equations (6.2) and (6.3) at
$\tilde {\mathcal G}=\{\tilde g_1, \ldots , \tilde g_k\}$
is generating for f. It follows from equations (6.2) and (6.3) at
![]() $x=a$
that
$x=a$
that
 $$ \begin{align} \bigg|h(a)-\sum_{l,n}a_{l,n} g_l(a)\bigg|<\epsilon \quad\text{and}\quad \bigg|\sum_{l,n}b_{l,n} g_l(a)\bigg|<\epsilon. \end{align} $$
$$ \begin{align} \bigg|h(a)-\sum_{l,n}a_{l,n} g_l(a)\bigg|<\epsilon \quad\text{and}\quad \bigg|\sum_{l,n}b_{l,n} g_l(a)\bigg|<\epsilon. \end{align} $$
Observe that
Combining equation (6.4) with equation (6.2), we obtain that
 $$ \begin{align*} &\bigg\|h-\sum_{l,n}a_{l,n}\tilde{g_l}\circ f^{2n}-\sum_{l,n}b_{l,n}\tilde{g_l}\circ f^{2n+1}\bigg\|_{[0,a], \infty} \\ &\quad= \bigg\|h-\sum_{l,n}a_{l,n}{g_l}\circ f^{2n}-\sum_{l,n}b_{l,n}{g_l}(a) \bigg\|_{[0,a] \infty} <2\epsilon. \end{align*} $$
$$ \begin{align*} &\bigg\|h-\sum_{l,n}a_{l,n}\tilde{g_l}\circ f^{2n}-\sum_{l,n}b_{l,n}\tilde{g_l}\circ f^{2n+1}\bigg\|_{[0,a], \infty} \\ &\quad= \bigg\|h-\sum_{l,n}a_{l,n}{g_l}\circ f^{2n}-\sum_{l,n}b_{l,n}{g_l}(a) \bigg\|_{[0,a] \infty} <2\epsilon. \end{align*} $$
Similarly, combining equation (6.4) with equation (6.3), we get
 $$ \begin{align*} &\bigg\|h-\sum_{l,n}a_{l,n}\tilde{g_l}\circ f^{2n}-\sum_{l,n}b_{l,n}\tilde{g_l}\circ f^{2n+1}\bigg\|_{[a,1], \infty} \\ &\quad= \bigg\|h-\sum_{l,n}a_{l,n}{g_l}(a)-\sum_{l,n}b_{l,n}{g_l}\circ f^{2n+1} \bigg\|_{[a,1] \infty} \\ &\quad\le \bigg|h(a)-\sum_{l,n}a_{l,n}{g_l}(a)\bigg|+ \bigg\| h-\sum_{l,n}b_{l,n}{g_l}\circ f^{2n+1} -h(a) \bigg\|_{[a,1] \infty} <2\epsilon. \end{align*} $$
$$ \begin{align*} &\bigg\|h-\sum_{l,n}a_{l,n}\tilde{g_l}\circ f^{2n}-\sum_{l,n}b_{l,n}\tilde{g_l}\circ f^{2n+1}\bigg\|_{[a,1], \infty} \\ &\quad= \bigg\|h-\sum_{l,n}a_{l,n}{g_l}(a)-\sum_{l,n}b_{l,n}{g_l}\circ f^{2n+1} \bigg\|_{[a,1] \infty} \\ &\quad\le \bigg|h(a)-\sum_{l,n}a_{l,n}{g_l}(a)\bigg|+ \bigg\| h-\sum_{l,n}b_{l,n}{g_l}\circ f^{2n+1} -h(a) \bigg\|_{[a,1] \infty} <2\epsilon. \end{align*} $$
Therefore, we have
 $$ \begin{align*}\bigg\|h-\sum_{l,n}a_{l,n}\tilde{g_l}\circ f^{2n}-\sum_{l,n}b_{l,n}\tilde{g_l}\circ f^{2n+1}\bigg\|_{\infty}<2\epsilon.\end{align*} $$
$$ \begin{align*}\bigg\|h-\sum_{l,n}a_{l,n}\tilde{g_l}\circ f^{2n}-\sum_{l,n}b_{l,n}\tilde{g_l}\circ f^{2n+1}\bigg\|_{\infty}<2\epsilon.\end{align*} $$
We conclude that
![]() $\tilde {\mathcal G}$
is generating for f as
$\tilde {\mathcal G}$
is generating for f as
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $h\in C([0,1])$
have been chosen arbitrarily.
$h\in C([0,1])$
have been chosen arbitrarily.
Question 6.6. What is the topological multiplicity of a Morse–Smale diffeomorphism?
6.0.4 Thue–Morse subshift
We give now an example of a uniquely ergodic system with mixed spectrum and simple topological multiplicity. The Thue–Morse subshift
![]() $X_{\zeta }$
is the bilateral subshift associated to the substitution
$X_{\zeta }$
is the bilateral subshift associated to the substitution
![]() $\zeta (0)=01$
and
$\zeta (0)=01$
and
![]() $\zeta (1)=10$
, that is,
$\zeta (1)=10$
, that is,
![]() $X_{\zeta }=X_u$
with u being the infinite word of
$X_{\zeta }=X_u$
with u being the infinite word of
![]() $\{0,1\}^{\mathbb {Z}}$
given by
$\{0,1\}^{\mathbb {Z}}$
given by
![]() $\cdots u_2u_1u_0u_0 u_1u_2\cdots $
with
$\cdots u_2u_1u_0u_0 u_1u_2\cdots $
with
![]() $u_0 u_1u_2\cdots $
being the unique fixed point of the substitution
$u_0 u_1u_2\cdots $
being the unique fixed point of the substitution
![]() $v_0v_1v_2\cdots \mapsto \zeta (v_0)\zeta (v_1)\zeta (v_2)\cdots $
. This subshift is known to be a minimal uniquely ergodic system with simple mixed spectrum (for the Koopman operator
$v_0v_1v_2\cdots \mapsto \zeta (v_0)\zeta (v_1)\zeta (v_2)\cdots $
. This subshift is known to be a minimal uniquely ergodic system with simple mixed spectrum (for the Koopman operator
![]() $U_{\sigma }$
on
$U_{\sigma }$
on
![]() $L^2_0(\nu )$
with
$L^2_0(\nu )$
with
![]() $\nu $
being the unique invariant probability measure) [Reference KwiatkowskiKwi81, Reference Michel, Conze and KeaneMic76]. The continuous part of its spectrum is singular with respect to the Lebesgue measure [Reference KakutaniKak72]. The map
$\nu $
being the unique invariant probability measure) [Reference KwiatkowskiKwi81, Reference Michel, Conze and KeaneMic76]. The continuous part of its spectrum is singular with respect to the Lebesgue measure [Reference KakutaniKak72]. The map
![]() $\tau : X_{\zeta }\rightarrow X_{\zeta }$
,
$\tau : X_{\zeta }\rightarrow X_{\zeta }$
,
![]() $(x_n)_{n\in \mathbb {Z}}\mapsto (1-x_n)_{n\in \mathbb {Z}}$
defines an involution of
$(x_n)_{n\in \mathbb {Z}}\mapsto (1-x_n)_{n\in \mathbb {Z}}$
defines an involution of
![]() $X_{\zeta }$
. As
$X_{\zeta }$
. As
![]() $\tau $
commutes with
$\tau $
commutes with
![]() $\sigma $
, the measure
$\sigma $
, the measure
![]() $\nu $
is also
$\nu $
is also
![]() $\tau $
-invariant.
$\tau $
-invariant.
Theorem 6.7. The Thue–Morse subshift is topologically simple.
For any
![]() $n\in \mathbb N$
, we let
$n\in \mathbb N$
, we let
![]() $\mathcal {F}_n=\{\chi _{[\zeta ^n(i)]}: i\in \{0,1\} \}$
and
$\mathcal {F}_n=\{\chi _{[\zeta ^n(i)]}: i\in \{0,1\} \}$
and
![]() $f_n=\chi _{[\zeta ^n(0)]}$
. To prove Theorem 6.7, we first show the following lemma which states that the space
$f_n=\chi _{[\zeta ^n(0)]}$
. To prove Theorem 6.7, we first show the following lemma which states that the space
![]() $V_{\mathcal F_n}$
is cyclic.
$V_{\mathcal F_n}$
is cyclic.
Lemma 6.8.
Proof. Fix
![]() $n\in \mathbb {N}$
. Notice that the (simple) point spectrum of
$n\in \mathbb {N}$
. Notice that the (simple) point spectrum of
![]() $U_{\sigma }$
consists in the powers of
$U_{\sigma }$
consists in the powers of
![]() $2$
. In particular, the system
$2$
. In particular, the system
![]() $(\zeta ^n(X), \sigma ^{2^n},{\mathcal B}, \nu )$
is ergodic, then the restriction of
$(\zeta ^n(X), \sigma ^{2^n},{\mathcal B}, \nu )$
is ergodic, then the restriction of
![]() $\sigma $
to
$\sigma $
to
![]() $\zeta ^n(X)$
is uniquely ergodic. Consequently, the Birkhoff sum
$\zeta ^n(X)$
is uniquely ergodic. Consequently, the Birkhoff sum
![]() $\frac {1}{p}\sum _{0\leq k<p }f_n\circ \sigma ^{k2^n}$
is converging uniformly to
$\frac {1}{p}\sum _{0\leq k<p }f_n\circ \sigma ^{k2^n}$
is converging uniformly to
![]() $\int f_n\, d\nu =\nu ([\zeta ^n(0)])$
on
$\int f_n\, d\nu =\nu ([\zeta ^n(0)])$
on
![]() $\zeta ^n(X)$
, when p goes to infinity. However,
$\zeta ^n(X)$
, when p goes to infinity. However,
![]() $\nu ([\zeta ^n(0)])=\nu ([\zeta ^n(1)])\neq 0$
. It follows that
$\nu ([\zeta ^n(0)])=\nu ([\zeta ^n(1)])\neq 0$
. It follows that
![]() $\chi _{[\zeta ^n(X)]} \in V_{\{f_n\}}$
. Since
$\chi _{[\zeta ^n(X)]} \in V_{\{f_n\}}$
. Since
![]() $\chi _{\zeta ^n(X)}=f_n+\chi _{[\zeta ^n(1)]}$
, we conclude that the continuous function
$\chi _{\zeta ^n(X)}=f_n+\chi _{[\zeta ^n(1)]}$
, we conclude that the continuous function
![]() $\chi _{[\zeta ^n(1)]}$
belongs to
$\chi _{[\zeta ^n(1)]}$
belongs to
![]() $V_{\{f_n\}}$
.
$V_{\{f_n\}}$
.
We are now in a position to prove Theorem 6.7. We make use of the following notation. For a point
![]() $x=(x_n)_{n\in \mathbb {Z}}$
, we write it as
$x=(x_n)_{n\in \mathbb {Z}}$
, we write it as
Proof of Theorem 6.7
According to Lemma 6.8, it is enough to check the assumptions of Lemma 4.1 with
![]() $(\mathcal F_n)_n$
. As the sequence of vectors spaces
$(\mathcal F_n)_n$
. As the sequence of vectors spaces
![]() $(V_{\mathcal F_n})_{n\in \mathcal {N}}$
is non-decreasing, one only needs to show
$(V_{\mathcal F_n})_{n\in \mathcal {N}}$
is non-decreasing, one only needs to show
![]() $\overline {\bigcup _n V_{\mathcal {F}_n}}=C(X_{\zeta })$
. If not, there would be distinct probability measures
$\overline {\bigcup _n V_{\mathcal {F}_n}}=C(X_{\zeta })$
. If not, there would be distinct probability measures
![]() $\mu ^{\pm }$
with
$\mu ^{\pm }$
with
Let
![]() $E=\{\zeta ^{\infty } (i). \zeta ^{\infty }(j): i,j \in \{0,1\}\}$
. Then for every n,
$E=\{\zeta ^{\infty } (i). \zeta ^{\infty }(j): i,j \in \{0,1\}\}$
. Then for every n,
is a partition of
![]() $X_{\zeta }\setminus O_{\sigma }(E)$
where
$X_{\zeta }\setminus O_{\sigma }(E)$
where
![]() $O_{\sigma }(E)$
is the orbit of E under
$O_{\sigma }(E)$
is the orbit of E under
![]() $\sigma $
, that is,
$\sigma $
, that is,
![]() $O_{\sigma }(E)=\{\sigma ^k(x): x\in E, k\in \mathbb {Z} \}$
. For any open set
$O_{\sigma }(E)=\{\sigma ^k(x): x\in E, k\in \mathbb {Z} \}$
. For any open set
![]() $U\supset {O_{\sigma }(E)} $
, we will show that
$U\supset {O_{\sigma }(E)} $
, we will show that
![]() $\mu ^+|_{X_{\zeta } \setminus U}= \mu ^-|_{X_{\zeta } \setminus U}$
. Obviously, we have
$\mu ^+|_{X_{\zeta } \setminus U}= \mu ^-|_{X_{\zeta } \setminus U}$
. Obviously, we have
Thus,
![]() $\{P_n\cap (X_{\zeta } \setminus U) \}_{n\in \mathbb {N}}$
generates Borel
$\{P_n\cap (X_{\zeta } \setminus U) \}_{n\in \mathbb {N}}$
generates Borel
![]() $\sigma $
-algebra on
$\sigma $
-algebra on
![]() $X_{\zeta } \setminus U$
. Therefore, we have
$X_{\zeta } \setminus U$
. Therefore, we have
![]() $\mu ^+|_{X_{\zeta } \setminus U}= \mu ^-|_{X_{\zeta } \setminus U}$
. Since U is chosen arbitrarily, we obtain that
$\mu ^+|_{X_{\zeta } \setminus U}= \mu ^-|_{X_{\zeta } \setminus U}$
. Since U is chosen arbitrarily, we obtain that
Let
which form a partition of E. Then by
![]() $\mu ^+([\zeta ^n(i)] )= \mu ^-([\zeta ^n(i)] )$
for all n, we have
$\mu ^+([\zeta ^n(i)] )= \mu ^-([\zeta ^n(i)] )$
for all n, we have
![]() $\mu ^+(E_i )= \mu ^-(E_i )$
. Similarly, we have
$\mu ^+(E_i )= \mu ^-(E_i )$
. Similarly, we have
![]() $\mu ^+(E^j )= \mu ^-(E^j )$
. Observe that
$\mu ^+(E^j )= \mu ^-(E^j )$
. Observe that
It follows that
![]() $\mu ^+(\zeta ^{\infty } (0). \zeta ^{\infty }(1))= \mu ^-(\zeta ^{\infty } (0). \zeta ^{\infty }(1)).$
Thus, we get
$\mu ^+(\zeta ^{\infty } (0). \zeta ^{\infty }(1))= \mu ^-(\zeta ^{\infty } (0). \zeta ^{\infty }(1)).$
Thus, we get
Similarly, we obtain
![]() $\mu ^+|_{\sigma ^k(E)}= \mu ^-|_{\sigma ^k(E)}$
for all
$\mu ^+|_{\sigma ^k(E)}= \mu ^-|_{\sigma ^k(E)}$
for all
![]() $k\in \mathbb {Z}$
. It implies that
$k\in \mathbb {Z}$
. It implies that
![]() $\mu ^+|_{{O_{\sigma }(E)}}= \mu ^-|_{{O_{\sigma }(E)}}.$
Combining this with equation (6.5), we conclude that
$\mu ^+|_{{O_{\sigma }(E)}}= \mu ^-|_{{O_{\sigma }(E)}}.$
Combining this with equation (6.5), we conclude that
![]() $\mu ^+= \mu ^-$
, which is a contradi- ction.
$\mu ^+= \mu ^-$
, which is a contradi- ction.
7 Subshifts with linear growth complexity
We consider a subshift
![]() $X\subset \mathcal A^{\mathbb {Z}}$
with letters in a finite alphabet
$X\subset \mathcal A^{\mathbb {Z}}$
with letters in a finite alphabet
![]() $\mathcal A$
. For
$\mathcal A$
. For
![]() $x\in \mathcal A^{\mathbb {Z}}$
, we denote by
$x\in \mathcal A^{\mathbb {Z}}$
, we denote by
![]() $x=(x_n)_{n\in \mathbb {Z}}$
for
$x=(x_n)_{n\in \mathbb {Z}}$
for
![]() $x_n\in \mathcal {A}$
. Let
$x_n\in \mathcal {A}$
. Let
![]() $\mathcal L_n(X)\subset \mathcal {A}^n$
be the finite words of X of length n, that is,
$\mathcal L_n(X)\subset \mathcal {A}^n$
be the finite words of X of length n, that is,
![]() $\mathcal L_n(X)=\{ x_k x_{k+1} \ldots x_{k+n-1}: x\in X, k\in \mathbb {Z} \}$
. The word complexity of X is given by
$\mathcal L_n(X)=\{ x_k x_{k+1} \ldots x_{k+n-1}: x\in X, k\in \mathbb {Z} \}$
. The word complexity of X is given by
We suppose that X is aperiodic and has linear growth, that is, for some
![]() $k\in \mathbb N^*$
,
$k\in \mathbb N^*$
,
Boshernitzan [Reference BoshernitzanBos92] showed that such a subshift admits at most k ergodic measures. By [Reference Donoso, Durand, Maass and PetiteDDMP21, Theorem 5.5], such subshifts, when assumed to be moreover minimal, have topological rank less than or equal to
![]() $(1+k\sharp \mathcal A^2)^{2(k+2)}$
. We show in this section the following upper bound on the topological multiplicity.
$(1+k\sharp \mathcal A^2)^{2(k+2)}$
. We show in this section the following upper bound on the topological multiplicity.
Theorem 7.1. Any aperiodic subshift X with
![]() $\liminf _{n\to \infty }({p_X(n)}/{n})\le k$
has topological multiplicity less than or equal to
$\liminf _{n\to \infty }({p_X(n)}/{n})\le k$
has topological multiplicity less than or equal to
![]() $2k$
.
$2k$
.
One may wonder if the upper bound in Theorem 7.1 is sharp.
Question 7.2. Is an aperiodic subshift X with
![]() $\liminf _{n\to \infty }({p_X(n)}/{n})=1$
topologically simple?
$\liminf _{n\to \infty }({p_X(n)}/{n})=1$
topologically simple?
To prove Theorem 7.1, we define some notation. Let
![]() $Q_n$
be the subset of
$Q_n$
be the subset of
![]() $\mathcal L_n(X)$
given by words w such that there are several letters
$\mathcal L_n(X)$
given by words w such that there are several letters
![]() $a\in \mathcal A$
with
$a\in \mathcal A$
with
![]() $wa\in \mathcal L_{n+1}(X)$
. We also let
$wa\in \mathcal L_{n+1}(X)$
. We also let
![]() $Q^{\prime }_{n+1}$
be the
$Q^{\prime }_{n+1}$
be the
![]() $(n+1)$
-words
$(n+1)$
-words
![]() $wa$
as above. Clearly, we have
$wa$
as above. Clearly, we have
Through this section, we always assume the subshift is aperiodic and satisfies the linear growth equation (7.1).
Lemma 7.3. The subset of integers
is infinite.
For the sake of completeness, we reproduce the proof, which is contained in [Reference BoshernitzanBos84, Theorem 2.2].
Proof. By equation (7.1), we have
It follows that
is an infinite set. For any
![]() $n\in {\mathcal M} $
, we have
$n\in {\mathcal M} $
, we have
However, for any
![]() $n\in {\mathcal M} $
, we get
$n\in {\mathcal M} $
, we get
This implies that
![]() ${\mathcal M} \subset {\mathcal N}$
. Therefore, the set
${\mathcal M} \subset {\mathcal N}$
. Therefore, the set
![]() ${\mathcal N}$
is infinite.
${\mathcal N}$
is infinite.
Lemma 7.4. [Reference BoshernitzanBos84, Lemma 4.1]
For any
![]() $n\in {\mathcal N}$
and
$n\in {\mathcal N}$
and
![]() $m\ge (k+2)(n+1)$
, any word
$m\ge (k+2)(n+1)$
, any word
![]() $w\in \mathcal {L}_m$
contains a subword in
$w\in \mathcal {L}_m$
contains a subword in
![]() $Q_n$
.
$Q_n$
.
For the sake of completeness, we provide a proof here.
Proof. We prove it by contradiction. Assume in contrast that all
![]() $(m - n + 1)$
n-subwords of w do not belong to
$(m - n + 1)$
n-subwords of w do not belong to
![]() $Q_n$
. That means that each of these n-blocks determines uniquely the next letter. Since
$Q_n$
. That means that each of these n-blocks determines uniquely the next letter. Since
![]() $m - n + 1 \ge 2(k+1)n> p_X(n)$
, at least one n-word appears more than one time as a subword of w. Therefore, X contains a periodic point, which contradicts our assumption.
$m - n + 1 \ge 2(k+1)n> p_X(n)$
, at least one n-word appears more than one time as a subword of w. Therefore, X contains a periodic point, which contradicts our assumption.
Now we show that any cylinder of length less than n can be decomposed as the cylinders of elements in
![]() $ Q^{\prime }_{n+1}$
after translations.
$ Q^{\prime }_{n+1}$
after translations.
Lemma 7.5. Let
![]() $n\in {\mathcal N}$
. Any cylinder
$n\in {\mathcal N}$
. Any cylinder
![]() $[w]$
with length of w less than n may be written uniquely as a finite disjoint union of sets of the form
$[w]$
with length of w less than n may be written uniquely as a finite disjoint union of sets of the form
![]() $\sigma ^{p}[q^{\prime }_{n+1}]$
with
$\sigma ^{p}[q^{\prime }_{n+1}]$
with
![]() $p\in \mathbb N$
,
$p\in \mathbb N$
,
![]() $q^{\prime }_{n+1}\in Q^{\prime }_{n+1}$
, such that
$q^{\prime }_{n+1}\in Q^{\prime }_{n+1}$
, such that
![]() $\sigma ^{t} [q^{\prime }_{n+1}]\cap [q_n]=\emptyset $
for any
$\sigma ^{t} [q^{\prime }_{n+1}]\cap [q_n]=\emptyset $
for any
![]() $0<t<p$
and any
$0<t<p$
and any
![]() $q_n\in Q_n$
.
$q_n\in Q_n$
.
Remark that by Lemma 7.4, the integer p belongs to
![]() $[0,(k+2)(n+1)]$
.
$[0,(k+2)(n+1)]$
.
Proof. Let
![]() $[w]$
be a cylinder associated to a word
$[w]$
be a cylinder associated to a word
![]() $w\in \mathcal L_l(X)$
with
$w\in \mathcal L_l(X)$
with
![]() $l<n$
. For
$l<n$
. For
![]() $x\in [w]$
, we let
$x\in [w]$
, we let
![]() $K_x\in {\mathbb {Z}}$
be the largest integer j less than l such that
$K_x\in {\mathbb {Z}}$
be the largest integer j less than l such that
![]() $x_{j-n+1}\cdots x_j$
belongs to
$x_{j-n+1}\cdots x_j$
belongs to
![]() $Q_n$
. Then the word
$Q_n$
. Then the word
![]() $w_{n+1}^x=x_{K_x-n+1}\cdots x_{K_x+1}$
belongs to
$w_{n+1}^x=x_{K_x-n+1}\cdots x_{K_x+1}$
belongs to
![]() $Q^{\prime }_{n+1}$
. Observe also that by Lemma 7.4, we have
$Q^{\prime }_{n+1}$
. Observe also that by Lemma 7.4, we have
![]() $n-1-K_x\leq (k+2)(n+1)$
. Let
$n-1-K_x\leq (k+2)(n+1)$
. Let
![]() $W_{n+1}$
be the collection of these words
$W_{n+1}$
be the collection of these words
![]() $w_{n+1}^x$
over
$w_{n+1}^x$
over
![]() $x\in [w]$
. By definition of
$x\in [w]$
. By definition of
![]() $K_x$
and
$K_x$
and
![]() $Q_n$
, the word
$Q_n$
, the word
![]() $w_{n+1}^x$
completely determines the
$w_{n+1}^x$
completely determines the
![]() $l-1-K_x$
next letters, that is to say,
$l-1-K_x$
next letters, that is to say,
As x belongs to
![]() $[w]$
, we have in particular
$[w]$
, we have in particular
![]() $\sigma ^{n-1-K_x}[w_{n+1}^x]\subset [w]$
and finally
$\sigma ^{n-1-K_x}[w_{n+1}^x]\subset [w]$
and finally
 $$ \begin{align*}[w]=\coprod_{w_{n+1}^x\in W_{n+1}} \sigma^{n-1-K_x}w^x_{n+1}.\end{align*} $$
$$ \begin{align*}[w]=\coprod_{w_{n+1}^x\in W_{n+1}} \sigma^{n-1-K_x}w^x_{n+1}.\end{align*} $$
We complete the proof.
Proof of Theorem 7.1
By equation (7.2) and the definition of
![]() ${\mathcal N}$
, we have for
${\mathcal N}$
, we have for
![]() $n\in {\mathcal N}$
,
$n\in {\mathcal N}$
,
 $$ \begin{align*} \sharp Q^{\prime}_{n+1}&=\sharp Q_n + p_X(n+1)-p_X(n)\\ &\le 2(p_X(n+1)-p_X(n))\\ &\le 2k. \end{align*} $$
$$ \begin{align*} \sharp Q^{\prime}_{n+1}&=\sharp Q_n + p_X(n+1)-p_X(n)\\ &\le 2(p_X(n+1)-p_X(n))\\ &\le 2k. \end{align*} $$
For
![]() $n\in {\mathcal N}$
, we let
$n\in {\mathcal N}$
, we let
![]() $F_n =\{\chi _{[q^{\prime }_{n+1}]}, q^{\prime }_{n+1}\in Q^{\prime }_{n+1}\}$
. By Lemma 7.5, any cylinder
$F_n =\{\chi _{[q^{\prime }_{n+1}]}, q^{\prime }_{n+1}\in Q^{\prime }_{n+1}\}$
. By Lemma 7.5, any cylinder
![]() $[w]$
with length less than n is a finite disjoint union of
$[w]$
with length less than n is a finite disjoint union of
![]() $\sigma ^{p}[q^{\prime }_{n+1}]$
. In particular,
$\sigma ^{p}[q^{\prime }_{n+1}]$
. In particular,
![]() $\chi _{[w]}$
lies in
$\chi _{[w]}$
lies in
![]() $V_{F_n}$
. We may therefore apply Lemma 4.1 to
$V_{F_n}$
. We may therefore apply Lemma 4.1 to
![]() $(F_n)_{n\in {\mathcal N}}$
and we get
$(F_n)_{n\in {\mathcal N}}$
and we get
7.1 Multiplicity of invariant measures
It follows from Theorem 7.1 and Lemma 2.4 that any ergodic measure has (ergodic) multiplicity bounded by
![]() $2k$
. In fact, we may refine this result as follows.
$2k$
. In fact, we may refine this result as follows.
Theorem 7.6. Let X be an aperiodic subshift with
![]() $\liminf _{n\to \infty }({p_X(n)}/{n})\le k$
. Then
$\liminf _{n\to \infty }({p_X(n)}/{n})\le k$
. Then
 $$ \begin{align*} \sum_{\mu\in {\mathcal M}_e(X,\sigma)}\mathrm{Mult}(\mu)\leq 2k. \end{align*} $$
$$ \begin{align*} \sum_{\mu\in {\mathcal M}_e(X,\sigma)}\mathrm{Mult}(\mu)\leq 2k. \end{align*} $$
To prove Theorem 7.6, we first recall some notation and then show two lemmas for general aperiodic subshifts. We have learned from the referee that some parts of our proofs overlap with results in [Reference CreutzCre23, Reference EspinozaEsp23]. Let
![]() $(Y,\sigma )$
be an aperiodic subshift. For two finite words w and v, we denote by
$(Y,\sigma )$
be an aperiodic subshift. For two finite words w and v, we denote by
![]() $N(w|v)$
the number of times that w appears as a subword of v. Also, we define
$N(w|v)$
the number of times that w appears as a subword of v. Also, we define
![]() $d(w|v)=N(w|v)/|v|$
. For a generic point x of a measure
$d(w|v)=N(w|v)/|v|$
. For a generic point x of a measure
![]() $\mu $
, we have
$\mu $
, we have
where
![]() $x_1^n=x_1x_2\ldots x_n$
. For a finite word v, we denote by
$x_1^n=x_1x_2\ldots x_n$
. For a finite word v, we denote by
![]() $v^{\otimes m}=\underbrace {vv \ldots v}_{m \text { times}}$
. For a finite word w, we denote by
$v^{\otimes m}=\underbrace {vv \ldots v}_{m \text { times}}$
. For a finite word w, we denote by
 $$ \begin{align*} \nu_w=\frac{1}{|w|}\sum_{k=0}^{|w|-1} \delta_{\sigma^k(\bar{w})}, \end{align*} $$
$$ \begin{align*} \nu_w=\frac{1}{|w|}\sum_{k=0}^{|w|-1} \delta_{\sigma^k(\bar{w})}, \end{align*} $$
where
![]() $|w|$
is the length of w and
$|w|$
is the length of w and
![]() $\bar {w}\in \mathcal {A}^{\mathbb {Z}}$
is the periodization of w, that is,
$\bar {w}\in \mathcal {A}^{\mathbb {Z}}$
is the periodization of w, that is,
![]() $w^{\otimes \infty }$
.
$w^{\otimes \infty }$
.
Let
![]() $w_n$
be a word of length n. Foy any n, we put
$w_n$
be a word of length n. Foy any n, we put
![]() $\ell _{n}=\ell (w_n):= \min \{1\le \ell <n: [w_{n}] \cap \sigma ^{\ell }([w_{n}])\not =\emptyset \}$
and
$\ell _{n}=\ell (w_n):= \min \{1\le \ell <n: [w_{n}] \cap \sigma ^{\ell }([w_{n}])\not =\emptyset \}$
and
![]() $L_{n}:=1+\sharp \{1\le \ell <n: [w_{n}] \cap \sigma ^{\ell }([w_{n}])\not =\emptyset \}$
, with the convention
$L_{n}:=1+\sharp \{1\le \ell <n: [w_{n}] \cap \sigma ^{\ell }([w_{n}])\not =\emptyset \}$
, with the convention
![]() $\min \emptyset =n$
. Let
$\min \emptyset =n$
. Let
![]() $v_{n}=v(w_n)$
be the first
$v_{n}=v(w_n)$
be the first
![]() $\ell _{n}$
-subword of
$\ell _{n}$
-subword of
![]() $w_{n}$
. It follows that
$w_{n}$
. It follows that
![]() $w_{n}= v_{n}^{\otimes K_{n}}\hat {v}_{n}$
with
$w_{n}= v_{n}^{\otimes K_{n}}\hat {v}_{n}$
with
![]() $\hat {v}_{n}\neq v_{n}$
being a prefix of
$\hat {v}_{n}\neq v_{n}$
being a prefix of
![]() $v_{n}$
. Then
$v_{n}$
. Then
![]() $K_{n}=\lfloor n/\ell _{n} \rfloor \geq L_{n}$
. Observe that for any
$K_{n}=\lfloor n/\ell _{n} \rfloor \geq L_{n}$
. Observe that for any
![]() $x\in X$
,
$x\in X$
,
![]() $p\geq \ell _{n}$
, and any word u of length less than
$p\geq \ell _{n}$
, and any word u of length less than
![]() $\ell _{n}$
, we have
$\ell _{n}$
, we have
 $$ \begin{align} N(u|x_1^p)&\geq N(u|w_{n}) \frac{N(w_{n}|x_1^p)}{L_{n}}\nonumber\\ &\geq N(u|v_{n}) K_{n} \frac{N(w_{n}|x_1^p)}{L_{n}}\nonumber\\ &\geq N(u|v_{n}) N(w_{n}|x_1^p). \end{align} $$
$$ \begin{align} N(u|x_1^p)&\geq N(u|w_{n}) \frac{N(w_{n}|x_1^p)}{L_{n}}\nonumber\\ &\geq N(u|v_{n}) K_{n} \frac{N(w_{n}|x_1^p)}{L_{n}}\nonumber\\ &\geq N(u|v_{n}) N(w_{n}|x_1^p). \end{align} $$
In the next two lemmas, we assume that:
-
• the subshift
 $(Y, \sigma )$
is aperiodic;
$(Y, \sigma )$
is aperiodic; -
•
 $w_n\in \mathcal {L}_n(Y)$
for
$w_n\in \mathcal {L}_n(Y)$
for
 $n\in \mathbb {N}$
;
$n\in \mathbb {N}$
; -
•
 $\nu _{w_n} \xrightarrow [n\in \mathcal {N}]{n\to +\infty }\nu \in \mathcal {M}_e(Y, \sigma )$
, that is,
$\nu _{w_n} \xrightarrow [n\in \mathcal {N}]{n\to +\infty }\nu \in \mathcal {M}_e(Y, \sigma )$
, that is,
 $\nu _{w_n}$
is weakly converging to an ergodic measure
$\nu _{w_n}$
is weakly converging to an ergodic measure
 $\nu $
when n goes to infinity along a subsequence
$\nu $
when n goes to infinity along a subsequence
 $\mathcal {N}$
.
$\mathcal {N}$
.
Lemma 7.7. Under the above assumption, we have
and
Proof. We argue by contradiction. Assume
![]() $(\ell _{n})_{n\in \mathbb {N}}$
has a bounded infinite subsequence
$(\ell _{n})_{n\in \mathbb {N}}$
has a bounded infinite subsequence
![]() $\mathcal {N}'$
of
$\mathcal {N}'$
of
![]() $\mathcal {N}$
. Then there are finite words v and
$\mathcal {N}$
. Then there are finite words v and
![]() $\hat {v}_n$
with
$\hat {v}_n$
with
![]() $|\hat {v}_n|<|v|$
such that
$|\hat {v}_n|<|v|$
such that
![]() $w_{n}= v^{\otimes K_{n}}\hat {v}_n$
for
$w_{n}= v^{\otimes K_{n}}\hat {v}_n$
for
![]() $n\in \mathcal {N}"$
, where
$n\in \mathcal {N}"$
, where
![]() $\mathcal {N}"$
is some infinite subsequence of
$\mathcal {N}"$
is some infinite subsequence of
![]() $\mathcal {N}'$
. Observe first that the length of
$\mathcal {N}'$
. Observe first that the length of
![]() $w_n$
goes to infinity. As a consequence,
$w_n$
goes to infinity. As a consequence,
![]() $K_n$
goes also to infinity as n goes to infinity along
$K_n$
goes also to infinity as n goes to infinity along
![]() $\mathcal {N}"$
. However, then X should contain the periodic point
$\mathcal {N}"$
. However, then X should contain the periodic point
![]() $\overline {v}$
associated to v which is a contradiction to the aperiodicity of
$\overline {v}$
associated to v which is a contradiction to the aperiodicity of
![]() $(Y, \sigma )$
. Therefore,
$(Y, \sigma )$
. Therefore,
![]() $\ell _{n}\xrightarrow [n\in \mathcal {N}]{n\to +\infty }+\infty $
.
$\ell _{n}\xrightarrow [n\in \mathcal {N}]{n\to +\infty }+\infty $
.
Let us check now that
![]() $\nu _{v_{n}}\xrightarrow [n\in \mathcal {N}]{n\to +\infty }\nu $
. Let
$\nu _{v_{n}}\xrightarrow [n\in \mathcal {N}]{n\to +\infty }\nu $
. Let
![]() $\nu '=\lim _{k\to \infty }\nu _{v_{n_k}}$
be a weak limit of
$\nu '=\lim _{k\to \infty }\nu _{v_{n_k}}$
be a weak limit of
![]() $(\nu _{v_{n}})_{n\in \mathcal {N}}$
with a subsequence
$(\nu _{v_{n}})_{n\in \mathcal {N}}$
with a subsequence
![]() $(n_k)_{k\in \mathbb {N}}$
of
$(n_k)_{k\in \mathbb {N}}$
of
![]() $\mathcal {N}$
. For any word u with
$\mathcal {N}$
. For any word u with
![]() $|u|<\ell _{n}$
, by equation (7.3), we have
$|u|<\ell _{n}$
, by equation (7.3), we have
and consequently,
 $$ \begin{align*} d(u|w_{n})&\geq d(u|v_{n}) \dfrac{K_{n}|v_{n}|}{(K_{n}+1)|v_{n}|}\\ &\geq \tfrac{1}{2}d(u|v_{n}). \end{align*} $$
$$ \begin{align*} d(u|w_{n})&\geq d(u|v_{n}) \dfrac{K_{n}|v_{n}|}{(K_{n}+1)|v_{n}|}\\ &\geq \tfrac{1}{2}d(u|v_{n}). \end{align*} $$
For any cylinder
![]() $[u]$
, by letting n go to infinity, we get that
$[u]$
, by letting n go to infinity, we get that
It implies that
![]() $\nu -\tfrac 12 \nu '$
is a
$\nu -\tfrac 12 \nu '$
is a
![]() $\sigma $
-invariant measure. It follows from the ergodicity of
$\sigma $
-invariant measure. It follows from the ergodicity of
![]() $\nu $
that
$\nu $
that
![]() $\nu =\nu '$
.
$\nu =\nu '$
.
Lemma 7.8. For any ergodic measure
![]() $\mu \not =\nu $
, we have
$\mu \not =\nu $
, we have
Proof. Assume
![]() $\limsup _{n \in {\mathcal N}, n\to \infty } |v_{n}| \mu ([w_{n}])>0.$
By passing to an infinite subsequence
$\limsup _{n \in {\mathcal N}, n\to \infty } |v_{n}| \mu ([w_{n}])>0.$
By passing to an infinite subsequence
![]() $\mathcal {N}'$
of
$\mathcal {N}'$
of
![]() $\mathcal {N}$
, we have
$\mathcal {N}$
, we have
![]() $\lim _{n\in \mathcal {N}', n\to \infty } |v_{n}| \mu ([w_{n}])=b>0 $
. By Lemma 7.7, the sequence
$\lim _{n\in \mathcal {N}', n\to \infty } |v_{n}| \mu ([w_{n}])=b>0 $
. By Lemma 7.7, the sequence
![]() $\nu _{v_{n}}$
,
$\nu _{v_{n}}$
,
![]() $n\in {\mathcal N}'$
, is converging to the measure
$n\in {\mathcal N}'$
, is converging to the measure
![]() $\nu $
.
$\nu $
.
Let x be a generic point of
![]() $\mu $
. Then we have for any n,
$\mu $
. Then we have for any n,
 $$ \begin{align} \lim_{p\to \infty} \frac{1}{p} \sum_{\ell=0}^{p-1} \chi_{[w_{n}]}(\sigma^{\ell}(x))= \lim_{p\to \infty} \frac{ N(w_{n}|x_1^p)}{p}=\mu([w_{n}]). \end{align} $$
$$ \begin{align} \lim_{p\to \infty} \frac{1}{p} \sum_{\ell=0}^{p-1} \chi_{[w_{n}]}(\sigma^{\ell}(x))= \lim_{p\to \infty} \frac{ N(w_{n}|x_1^p)}{p}=\mu([w_{n}]). \end{align} $$
In particular, for any n, we can choose
![]() $P_n\in \mathbb {N}$
such that for
$P_n\in \mathbb {N}$
such that for
![]() $p\geq P_n$
,
$p\geq P_n$
,
 $$ \begin{align} \frac{ N(w_{n}|x_1^p)}{p}\geq \frac{\mu([w_{n}])}{2}. \end{align} $$
$$ \begin{align} \frac{ N(w_{n}|x_1^p)}{p}\geq \frac{\mu([w_{n}])}{2}. \end{align} $$
Pick an arbitrary cylinder
![]() $[u]$
. By Lemma 7.7, there exists an integer N such that for
$[u]$
. By Lemma 7.7, there exists an integer N such that for
![]() $n>N$
, we have
$n>N$
, we have
It follows from equation (7.3) that
By letting p then
![]() $n\in {\mathcal N}'$
go to infinity, we get for any cylinder
$n\in {\mathcal N}'$
go to infinity, we get for any cylinder
![]() $[u]$
,
$[u]$
,
It implies that
![]() $\mu -({b}/{4}) \nu $
is a
$\mu -({b}/{4}) \nu $
is a
![]() $\sigma $
-invariant measure, which is a contradiction to the ergodicity of
$\sigma $
-invariant measure, which is a contradiction to the ergodicity of
![]() $\mu $
.
$\mu $
.
We recall now briefly the proof of Boshernitzan that an aperiodic subshift of linear growth has finite many ergodic measures. Let
![]() $\mathcal {N}$
be the infinite set as in Lemma 7.3. For any
$\mathcal {N}$
be the infinite set as in Lemma 7.3. For any
![]() $n\in \mathcal {N}$
, one can choose (not uniquely) an ordered k-tuple of n-words
$n\in \mathcal {N}$
, one can choose (not uniquely) an ordered k-tuple of n-words
![]() $K_n:=\{q_{n,1}, \ldots , q_{n,k}\}$
which coincides with
$K_n:=\{q_{n,1}, \ldots , q_{n,k}\}$
which coincides with
![]() $Q_n$
. By passing to a subsequence
$Q_n$
. By passing to a subsequence
![]() $\mathcal {N}'$
of
$\mathcal {N}'$
of
![]() $\mathcal {N}$
, we can make each of the sequences of
$\mathcal {N}$
, we can make each of the sequences of
![]() $\nu _{q_{n,i}}$
weakly converge to some measures
$\nu _{q_{n,i}}$
weakly converge to some measures
![]() $\mu _i \in \mathcal {M}(X,T)$
. Boshernitzan showed that
$\mu _i \in \mathcal {M}(X,T)$
. Boshernitzan showed that
Since
![]() $\mu _i$
may coincide with the other
$\mu _i$
may coincide with the other
![]() $\mu _j$
for
$\mu _j$
for
![]() $j\not =i$
, we define
$j\not =i$
, we define
![]() $I_i=\{1\le j\le k: \mu _j=\mu _i \}$
.
$I_i=\{1\le j\le k: \mu _j=\mu _i \}$
.
We will use the following complement of Lemma 7.5.
Lemma 7.9. In the decomposition of a cylinder
![]() $[w]$
given by Lemma 7.5, for any term
$[w]$
given by Lemma 7.5, for any term
![]() $\sigma ^p[q^{\prime }_{n+1}]$
with
$\sigma ^p[q^{\prime }_{n+1}]$
with
![]() $|v(q^{\prime }_{n+1})|<n+1$
, we have
$|v(q^{\prime }_{n+1})|<n+1$
, we have
![]() $p\leq |v(q^{\prime }_{n+1})|$
.
$p\leq |v(q^{\prime }_{n+1})|$
.
Proof. We argue by contradiction. To simplify the notation, we write
![]() $v_{n}=v(q^{\prime }_{n+1})$
. Assume
$v_{n}=v(q^{\prime }_{n+1})$
. Assume
![]() $|v_n|<n+1$
and
$|v_n|<n+1$
and
![]() $p> |v_{n}|$
. By definition of
$p> |v_{n}|$
. By definition of
![]() $v_n$
, we have
$v_n$
, we have
However, it follows from Lemma 7.5 that
![]() $\sigma ^{p}[q^{\prime }_{n+1}]$
does not intersect
$\sigma ^{p}[q^{\prime }_{n+1}]$
does not intersect
![]() $\sigma ^{l}(\bigcup _{q_n\in Q_n}[q_{n}])$
for
$\sigma ^{l}(\bigcup _{q_n\in Q_n}[q_{n}])$
for
![]() $0< l< p $
, therefore, with
$0< l< p $
, therefore, with
![]() $q_n\in Q_n$
being the prefix of
$q_n\in Q_n$
being the prefix of
![]() $q^{\prime }_{n+1}$
, we get the contradiction
$q^{\prime }_{n+1}$
, we get the contradiction
Thus, we have
![]() $p\leq |v(q^{\prime }_{n+1})|$
.
$p\leq |v(q^{\prime }_{n+1})|$
.
For a given i, we let
![]() $(q^l_{n,i})_{l\in \mathcal {Q}_{n,i}}$
be the elements of
$(q^l_{n,i})_{l\in \mathcal {Q}_{n,i}}$
be the elements of
![]() $Q^{\prime }_{n+1}$
with prefix
$Q^{\prime }_{n+1}$
with prefix
![]() $q_{n,i}$
, where
$q_{n,i}$
, where
![]() $\mathcal {Q}_{n,i}$
is a subset of
$\mathcal {Q}_{n,i}$
is a subset of
![]() $\mathcal {A}$
for each
$\mathcal {A}$
for each
![]() $n\in \mathcal {N}', 1\le i\le k$
. Note that
$n\in \mathcal {N}', 1\le i\le k$
. Note that
![]() $\nu _{q^l_{n,i}}$
is also converging to
$\nu _{q^l_{n,i}}$
is also converging to
![]() $\mu _i$
for any l when n goes to infinity along
$\mu _i$
for any l when n goes to infinity along
![]() $\mathcal {N}'$
. Finally, we let
$\mathcal {N}'$
. Finally, we let
![]() $v_{n,i}^l=v_n(q^l_{n,i})$
for each
$v_{n,i}^l=v_n(q^l_{n,i})$
for each
![]() $n\in \mathcal {N}', 1\le i\le k$
, and
$n\in \mathcal {N}', 1\le i\le k$
, and
![]() $l\in \mathcal {Q}_{n,i}$
.
$l\in \mathcal {Q}_{n,i}$
.
Proof of Theorem 7.6
Pick an arbitrary cylinder
![]() $[w]$
. Let
$[w]$
. Let
 $$ \begin{align*} [w]=\coprod_{j,l} \coprod_{\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l] \end{align*} $$
$$ \begin{align*} [w]=\coprod_{j,l} \coprod_{\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l] \end{align*} $$
be the decomposition of
![]() $[w]$
given by Lemma 7.5. Recall that
$[w]$
given by Lemma 7.5. Recall that
![]() $P_{j,l}$
is a subset of
$P_{j,l}$
is a subset of
![]() $ [0,(k+2) (n+1)]$
for any l and by Lemma 7.9, we have also
$ [0,(k+2) (n+1)]$
for any l and by Lemma 7.9, we have also
![]() $P_{j,l}\subset [0,|v^{l}_{n,j}|-1]$
if
$P_{j,l}\subset [0,|v^{l}_{n,j}|-1]$
if
![]() $|v^{l}_{n,j}|<n+1$
. For each
$|v^{l}_{n,j}|<n+1$
. For each
![]() $n\in \mathcal {N}'$
, we decompose
$n\in \mathcal {N}'$
, we decompose
![]() $\{(j,l):1\le j\le k, l\in \mathcal {Q}_{n,j}\}$
into three sets
$\{(j,l):1\le j\le k, l\in \mathcal {Q}_{n,j}\}$
into three sets
![]() $J_{n,i}$
,
$J_{n,i}$
,
![]() $J_{n,i}^{\prime }$
, and
$J_{n,i}^{\prime }$
, and
![]() $J_{n,i}^{\prime \prime }$
, where
$J_{n,i}^{\prime \prime }$
, where
![]() $J_{n,i}:=\{(j,l):j\in I_i\}$
,
$J_{n,i}:=\{(j,l):j\in I_i\}$
,
![]() $J_{n,i}^{\prime }:=\{(j,l): j\notin I_i, |v^{l}_{n,j}|=n+1 \}$
and
$J_{n,i}^{\prime }:=\{(j,l): j\notin I_i, |v^{l}_{n,j}|=n+1 \}$
and
![]() $J_{n,i}^{\prime \prime }$
is the rest. Then for
$J_{n,i}^{\prime \prime }$
is the rest. Then for
![]() $(j,l)\in J_{n,i}^{\prime }$
, we have
$(j,l)\in J_{n,i}^{\prime }$
, we have
 $$ \begin{align} \mu_i\bigg(\coprod_{p\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l]\bigg)\le (k+2)(n+1) \mu_i([q_{n,j}^l]) = (k+2) |v^{l}_{n,j}|\mu_i([q_{n,j}^l]). \end{align} $$
$$ \begin{align} \mu_i\bigg(\coprod_{p\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l]\bigg)\le (k+2)(n+1) \mu_i([q_{n,j}^l]) = (k+2) |v^{l}_{n,j}|\mu_i([q_{n,j}^l]). \end{align} $$
However, for
![]() $(j,l)\in J_{n,i}^{\prime \prime }$
, we have
$(j,l)\in J_{n,i}^{\prime \prime }$
, we have
 $$ \begin{align} \mu_i\bigg(\coprod_{p\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l]\bigg)\le |v^{l}_{n,j}|\mu_i([q_{n,j}^l]). \end{align} $$
$$ \begin{align} \mu_i\bigg(\coprod_{p\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l]\bigg)\le |v^{l}_{n,j}|\mu_i([q_{n,j}^l]). \end{align} $$
By summing up equations (7.7) and (7.8), we have
 $$ \begin{align} \mu_i\bigg(\coprod_{(j,l)\in J_{n,i}^{\prime}\cup J_{n,i}^{\prime\prime}} \coprod_{p\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l]\bigg)\le 2k(k+2) \sum_{(j,l)\in J_{n,i}^{\prime}\cup J_{n,i}^{\prime\prime}} |v^{l}_{n,j}|\mu_i([q_{n,j}^l]). \end{align} $$
$$ \begin{align} \mu_i\bigg(\coprod_{(j,l)\in J_{n,i}^{\prime}\cup J_{n,i}^{\prime\prime}} \coprod_{p\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l]\bigg)\le 2k(k+2) \sum_{(j,l)\in J_{n,i}^{\prime}\cup J_{n,i}^{\prime\prime}} |v^{l}_{n,j}|\mu_i([q_{n,j}^l]). \end{align} $$
Combining this with Lemma 7.8, we obtain
 $$ \begin{align*} \lim_{n\to \infty}\mu_i\bigg(\coprod_{(j,l)\in J_{n,i}^{\prime}\cup J_{n,i}^{\prime\prime}} \coprod_{p\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l]\bigg)=0. \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty}\mu_i\bigg(\coprod_{(j,l)\in J_{n,i}^{\prime}\cup J_{n,i}^{\prime\prime}} \coprod_{p\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l]\bigg)=0. \end{align*} $$
Therefore, we have
 $$ \begin{align*} &\bigg\|\chi_{[w]}-\!\sum_{(n,j)\in J_{n,i}, p\in P_{n,j}^l} \chi_{[q_{n,j}^l]}\circ \sigma^{-p}\bigg\|^2_{L^2(\mu_i)}\! = \|\chi_{[w]}-\chi_{\coprod_{(n,j)\in J_{n,i}, p\in P_{n,j}^l} \sigma^p[q_{n,j}^l]}\|^2_{L^2(\mu_i)}\\ &\quad= \mu_i\bigg(\coprod_{(j,l)\in J_{n,i}^{\prime}\cup J_{n,i}^{\prime\prime}} \coprod_{p\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l]\bigg)\xrightarrow[n\in \mathcal{N}']{n\to +\infty}0. \end{align*} $$
$$ \begin{align*} &\bigg\|\chi_{[w]}-\!\sum_{(n,j)\in J_{n,i}, p\in P_{n,j}^l} \chi_{[q_{n,j}^l]}\circ \sigma^{-p}\bigg\|^2_{L^2(\mu_i)}\! = \|\chi_{[w]}-\chi_{\coprod_{(n,j)\in J_{n,i}, p\in P_{n,j}^l} \sigma^p[q_{n,j}^l]}\|^2_{L^2(\mu_i)}\\ &\quad= \mu_i\bigg(\coprod_{(j,l)\in J_{n,i}^{\prime}\cup J_{n,i}^{\prime\prime}} \coprod_{p\in P_{n,j}^l} \sigma^{p}[q_{n,j}^l]\bigg)\xrightarrow[n\in \mathcal{N}']{n\to +\infty}0. \end{align*} $$
Thus, we can apply Lemma 4.1 in
![]() $L^2_0(\mu _i)$
with
$L^2_0(\mu _i)$
with
![]() $F_n =\{ \chi _{[q_{n,j}^l]} \ : \ (j,l)\in J_{n,i}\}$
to get
$F_n =\{ \chi _{[q_{n,j}^l]} \ : \ (j,l)\in J_{n,i}\}$
to get
By summing it up, we conclude that
 $$ \begin{align*} \sum_{\mu\in {\mathcal M}_e(X,\sigma)}\mathrm{Mult}(\mu) &\leq \sum_i \liminf_{n\in \mathcal{N}', n\to \infty} \sharp J_{n,i}\\ &\leq \liminf_{n\in \mathcal{N}', n\to \infty} \sharp Q^{\prime}_{n+1}\\ &\leq 2k.\\[-2.8pc] \end{align*} $$
$$ \begin{align*} \sum_{\mu\in {\mathcal M}_e(X,\sigma)}\mathrm{Mult}(\mu) &\leq \sum_i \liminf_{n\in \mathcal{N}', n\to \infty} \sharp J_{n,i}\\ &\leq \liminf_{n\in \mathcal{N}', n\to \infty} \sharp Q^{\prime}_{n+1}\\ &\leq 2k.\\[-2.8pc] \end{align*} $$