Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T11:15:26.048Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple correlation sequences not approximable by nilsequences

Part of: Sequences and sets

Published online by Cambridge University Press:  16 July 2021

JOP BRIËT  and
BEN GREEN Open the ORCID record for BEN GREEN [Opens in a new window]
JOP BRIËT
Affiliation:
Centrum Wiskunde & Informatica (CWI), Science Park 123, 1098XG, Amsterdam, The Netherlands (e-mail: [email protected])
BEN GREEN*
Affiliation:
Mathematical Institute, Andrew Wiles Building, Radcliffe Observatory Quarter, Woodstock Rd, OxfordOX2 6QW, UK
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that there is a measure-preserving system 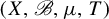$(X,\mathscr {B}, \mu , T)$ together with functions 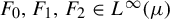$F_0, F_1, F_2 \in L^{\infty }(\mu )$ such that the correlation sequence 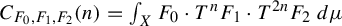$C_{F_0, F_1, F_2}(n) = \int _X F_0 \cdot T^n F_1 \cdot T^{2n} F_2 \, d\mu $ is not an approximate integral combination of 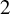$2$ -step nilsequences.

Keywords

multiplerecurrencenilsequence

MSC classification

Primary: 11B30: Arithmetic combinatorics; higher degree uniformity
Secondary: 11B25: Arithmetic progressions
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 9 , September 2022 , pp. 2711 - 2722
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Altman, D.. On Szemerédi’s theorem with differences from a random set. Acta Arith. 195(1) (2020), 97–108.CrossRefGoogle Scholar
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences. Invent. Math. 160(2) (2005), 261–303.CrossRefGoogle Scholar
Bergelson, V. and Leibman, A.. Distribution of values of bounded generalised polynomials. Acta Math. 198(2) (2007), 155–230.CrossRefGoogle Scholar
Briët, J. and Gopi, S.. Gaussian width bounds with applications to arithmetic progressions in random settings. Int. Math. Res. Not. 22 (2020), 8673–8696.Google Scholar
Briët, J. and Labib, F.. High-entropy dual functions over finite fields and locally decodable codes. Forum Math. Sigma 9 (2021), e19.CrossRefGoogle Scholar
Frantzikinakis, N.. Equidistribution of sparse sequences on nilmanifolds. J. Anal. Math. 109 (2009), 353–395.CrossRefGoogle Scholar
Frantzikinakis, N.. Some open problems on multiple ergodic averages. Bull. Hellenic Math. Soc. 60 (2016), 41–90.Google Scholar
Frantzikinakis, N.. An averaged Chowla and Elliott conjecture along independent polynomials. Int. Math. Res. Not. (IMRN) 12 (2018), 3721–3743.Google Scholar
Yekhanin, S.. Towards 3-query locally decodable codes of subexponential length. J. ACM 55(1) (2008), Art. 1, 16 pp.CrossRefGoogle Scholar