Hostname: page-component-6bf8c574d5-b4m5d Total loading time: 0 Render date: 2025-02-17T16:06:54.991Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimally critical regular endomorphisms of 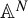$\mathbb{A}^N$

Part of: Arithmetic and non-Archimedean dynamical systems

Published online by Cambridge University Press:  21 October 2021

PATRICK INGRAM
PATRICK INGRAM*
Affiliation:
Department of Mathematics and Statistics, York University, Toronto, ON, Canada
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the dynamics of the map 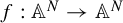$f:\mathbb {A}^N\to \mathbb {A}^N$ defined by

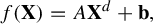$$ \begin{align*} f(\mathbf{X})=A\mathbf{X}^d+\mathbf{b}, \end{align*} $$

for 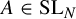$A\in \operatorname {SL}_N$ , 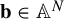$\mathbf {b}\in \mathbb {A}^N$ , and 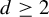$d\geq 2$ , a class which specializes to the unicritical polynomials when 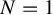$N=1$ . In the case $k=\mathbb {C}$ we obtain lower bounds on the sum of Lyapunov exponents of f, and a statement which generalizes the compactness of the Mandelbrot set. Over 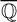$\overline {\mathbb {Q}}$ we obtain estimates on the critical height of f, and over algebraically closed fields we obtain some rigidity results for post-critically finite morphisms of this form.

Keywords

critical heightLyapunov exponentsarithmetic dynamics

MSC classification

Primary: 37P30: Height functions; Green functions; invariant measures
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 2 , February 2023 , pp. 585 - 614
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Bassanelli, G. and Berteloot, F.. Bifurcation currents in holomorphic dynamics on ${\mathbb{P}}^k$ . J. Reine Angew. Math. 608 (2007), 201–235.Google Scholar
Bedford, E. and Jonsson, M.. Dynamics of regular polynomial endomorphisms of ${\mathbf{C}}^k$ . Amer. J. Math. 122(1) (2000), 153–212.CrossRefGoogle Scholar
Benedetto, R. L., Ingram, P., Jones, R. and Levy, A.. Attracting cycles in $p$ -adic dynamics and height bounds for post-critically finite maps. Duke Math. J. 163(13) (2014), 2325–2356.Google Scholar
Bombieri, E. and Gubler, W.. Heights in Diophantine Geometry (New Mathematical Monographs, 4). Cambridge University Press, Cambridge, 2006.Google Scholar
Dinh, T. C. and Sibony, N.. Dynamique des applications d’allure polynomiale. J. Math. Pures Appl. (9) 82(4) (2003), 367–423.CrossRefGoogle Scholar
Faltings, G.. Diophantine approximation on abelian varieties. Ann. of Math (2) 133(3) (1991), 549–576.CrossRefGoogle Scholar
Favre, C.. Degeneration of endomorphisms of the complex projective space in the hybrid space. J. Inst. Math. Jussieu 19(4) (2020), 1141–1183.CrossRefGoogle Scholar
Ingram, P.. A finiteness result for post-critically finite polynomials. Int. Math. Res. Not. IMRN 2012(3) (2012), 524–543.CrossRefGoogle Scholar
Ingram, P.. Rigidity and height bounds for certain post-critically finite endomorphisms of ${\mathbb{P}}^N$ . Canadian J. Math. 68 (2016), 625–654.CrossRefGoogle Scholar
Ingram, P.. The critical height is a moduli height. Duke Math. J. 167(7) (2018), 1311–1346.CrossRefGoogle Scholar
Ingram, P.. Minimally critical endomorphisms of ${\mathbb{P}}^N$ . Preprint, 2020, arXiv:2006.12869.CrossRefGoogle Scholar
Ingram, P.. Explicit heights of divisors relative to endomorphisms of ${\mathbb{P}}^N$ , in preparation.Google Scholar
Ingram, P., Ramadas, R. and Silverman, J. H.. Post-critically finite maps on ${\mathbb{P}}^n$ for $n \geq 2$ are sparse. Preprint, 2019, arXiv:1910.11290.Google Scholar
Lang, S.. Algebra (Graduate Texts in Mathematics, 211), 3rd edn. Springer, New York, 2002.CrossRefGoogle Scholar
Mahler, K.. On some inequalities for polynomials in several variables. J. Lond. Math. Soc. (2) 37 (1962), 341–344.CrossRefGoogle Scholar
McMullen, C. T.. Families of rational maps and iterative root-finding algorithms. Ann. of Math. (2) 125(3) (1987), 467–493.Google Scholar
Philippon, P.. Sur des hauteurs alternatives. I. Math. Ann. 289(2) (1991), 255–283.CrossRefGoogle Scholar
Rosser, J. B. and Schoenfeld, L.. Approximate formulas for some functions of prime numbers. Illinois J. Math. 6(1) (1962), 64–94.CrossRefGoogle Scholar
Silverman, J. H.. Moduli Spaces and Arithmetic Dynamics (CRM Monograph Series, 30). American Mathematical Society, Providence, RI, 2012.CrossRefGoogle Scholar
Soulé, C.. Géométrie d’Arakelov et théorie des nombres transcendants. Astérisque 198–200 (1991), 355–371.Google Scholar
Zhang, S. W.. Small points and adelic metrics. J. Algebraic Geom. 4(2) (1995), 281–300.Google Scholar