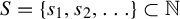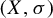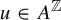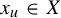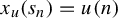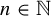1. Introduction
The well-known Sarnak conjecture states that the Möbius function
![]() $\mu $
is uncorrelated with all deterministic sequences. A sequence is called deterministic if it is the image under a continuous function of the trajectory of a point in a topological dynamical system with zero entropy (see §2 for definitions of this and other concepts not defined in this introduction). More formally, we state the Sarnak conjecture.
$\mu $
is uncorrelated with all deterministic sequences. A sequence is called deterministic if it is the image under a continuous function of the trajectory of a point in a topological dynamical system with zero entropy (see §2 for definitions of this and other concepts not defined in this introduction). More formally, we state the Sarnak conjecture.
Conjecture 1.1. (Sarnak conjecture)
If
![]() $(X,T)$
is a topological dynamical system with zero entropy,
$(X,T)$
is a topological dynamical system with zero entropy,
![]() $x_0 \in X$
, and
$x_0 \in X$
, and
![]() $f \in C(X)$
, then
$f \in C(X)$
, then
 $$ \begin{align*} \frac{1}{N} \sum_{n=1}^N \mu(n) f(T^n x_0) \rightarrow 0. \end{align*} $$
$$ \begin{align*} \frac{1}{N} \sum_{n=1}^N \mu(n) f(T^n x_0) \rightarrow 0. \end{align*} $$
Although this problem is still open, there are many recent works on the topic, which have made significant progress and resolved it for some classes of dynamical systems. In [Reference Eisner1], a potential stronger ‘polynomial’ (meaning that only polynomial iterates of
![]() $x_0$
are taken rather than all) version of the Sarnak conjecture was conjectured. To rule out some degenerate examples, the assumption of minimality was added on
$x_0$
are taken rather than all) version of the Sarnak conjecture was conjectured. To rule out some degenerate examples, the assumption of minimality was added on
![]() $(X, T)$
, meaning that for every
$(X, T)$
, meaning that for every
![]() $x \in X$
, the set
$x \in X$
, the set
![]() $\{T^n x\}$
is dense.
$\{T^n x\}$
is dense.
Conjecture 1.2. (Polynomial Sarnak conjecture [Reference Eisner1, Conjecture 2.3])
If
![]() $(X,T)$
is a minimal topological dynamical system with zero entropy,
$(X,T)$
is a minimal topological dynamical system with zero entropy,
![]() $x_0 \in X$
,
$x_0 \in X$
,
![]() $f \in C(X)$
, and
$f \in C(X)$
, and
![]() $p: \mathbb {N} \rightarrow \mathbb {N}_0$
is a polynomial, then
$p: \mathbb {N} \rightarrow \mathbb {N}_0$
is a polynomial, then
 $$ \begin{align*} \frac{1}{N} \sum_{n=1}^N \mu(n) f(T^{p(n)} x_0) \rightarrow 0. \end{align*} $$
$$ \begin{align*} \frac{1}{N} \sum_{n=1}^N \mu(n) f(T^{p(n)} x_0) \rightarrow 0. \end{align*} $$
This conjecture is now known to be false; recently, Kanigowski, Lemańczyk, and Radziwiłł[Reference Kanigowski, Lemańczyk and Radziwiłł4] and Lian and Shi [Reference Lian and Shi6] have separately provided counterexamples. The counterexamples from [Reference Lian and Shi6] are symbolically defined dynamical systems called Toeplitz subshifts, are specific to the case
![]() $p(n) = n^2$
(though they could perhaps be generalized), and attain correlation with
$p(n) = n^2$
(though they could perhaps be generalized), and attain correlation with
![]() $\mu $
arbitrarily close (but not equal to)
$\mu $
arbitrarily close (but not equal to)
![]() $1$
. The counterexamples from [Reference Kanigowski, Lemańczyk and Radziwiłł4] are skew products on manifolds, and although stated explicitly only for
$1$
. The counterexamples from [Reference Kanigowski, Lemańczyk and Radziwiłł4] are skew products on manifolds, and although stated explicitly only for
![]() $p(n) = n^2$
, they can be applied to a much larger class called ‘almost sparse sequences’ (which includes the primes). Both constructions make strong usage of arithmetic properties of the Möbius function, but can be generalized to other arithmetic functions.
$p(n) = n^2$
, they can be applied to a much larger class called ‘almost sparse sequences’ (which includes the primes). Both constructions make strong usage of arithmetic properties of the Möbius function, but can be generalized to other arithmetic functions.
The purpose of this note is to show that even much weaker versions of Conjecture 1.2 are false, because minimal zero entropy systems can achieve any possible behavior (that is, not just correlation with
![]() $\mu $
) along any prescribed set
$\mu $
) along any prescribed set
![]() $S \subset \mathbb {N}$
of zero Banach density (that is, not just the image of a polynomial). One such result had already been proved by the author in [Reference Pavlov7], which already immediately refutes the polynomial Sarnak conjecture.
$S \subset \mathbb {N}$
of zero Banach density (that is, not just the image of a polynomial). One such result had already been proved by the author in [Reference Pavlov7], which already immediately refutes the polynomial Sarnak conjecture.
Theorem 1.3. [Reference Pavlov7, Corollary 5.1]
Assume that
![]() $d \in \mathbb {N}$
,
$d \in \mathbb {N}$
,
![]() $(w_n)$
is an increasing sequence of positive integers where
$(w_n)$
is an increasing sequence of positive integers where
![]() $w_{n+1} < (w_{n+1} - w_n)^{d+1}$
for large enough n, and
$w_{n+1} < (w_{n+1} - w_n)^{d+1}$
for large enough n, and
![]() $(z_n)$
is any sequence in
$(z_n)$
is any sequence in
![]() $\mathbb {T} := \mathbb {Z}/\mathbb {N}$
. Then there exists a totally minimal, totally uniquely ergodic, topologically mixing zero entropy map S on
$\mathbb {T} := \mathbb {Z}/\mathbb {N}$
. Then there exists a totally minimal, totally uniquely ergodic, topologically mixing zero entropy map S on
![]() $\mathbb {T}^{2d+4}$
so that if
$\mathbb {T}^{2d+4}$
so that if
![]() $\pi $
is projection onto the final coordinate,
$\pi $
is projection onto the final coordinate,
![]() $\pi (S^{w_n} \mathbf {0}) = z_n$
for sufficiently large n.
$\pi (S^{w_n} \mathbf {0}) = z_n$
for sufficiently large n.
(We do not further work with the properties of unique ergodicity and topological mixing, and so do not provide definitions here. However, we do note that Theorem 1.3 shows that even adding these hypotheses to Conjecture 1.2 would not make it true.) We note that the entropy of the transformation S was never mentioned in [Reference Pavlov7]. However, S is defined as a suspension flow of a product of a toral rotation and a skew product T under a roof function
![]() $1 < g < 3$
. The skew product T is of the form
$1 < g < 3$
. The skew product T is of the form
![]() $(x_1, x_2, x_3, \ldots , x_m) \mapsto (x_1 + \alpha , x_2 + f(x_1), x_3 + x_2, \ldots , x_m + x_{m-1})$
for a continuous self-map f of
$(x_1, x_2, x_3, \ldots , x_m) \mapsto (x_1 + \alpha , x_2 + f(x_1), x_3 + x_2, \ldots , x_m + x_{m-1})$
for a continuous self-map f of
![]() $\mathbb {T}$
. Since its first coordinate is an irrational rotation, known to have zero entropy, the map T also has zero entropy by Abramov’s skew product entropy formula. Then S has zero entropy as well, by Abramov’s suspension flow entropy formula.
$\mathbb {T}$
. Since its first coordinate is an irrational rotation, known to have zero entropy, the map T also has zero entropy by Abramov’s skew product entropy formula. Then S has zero entropy as well, by Abramov’s suspension flow entropy formula.
Remark 1.4. Here are a few more relevant facts about the construction from [Reference Pavlov7].
-
(1) The map S is distal, meaning that for all
 $x \neq y$
,
$x \neq y$
,
 $\{d(T^n x, T^n y)\}_n$
is bounded away from
$\{d(T^n x, T^n y)\}_n$
is bounded away from
 $0$
.
$0$
. -
(2) The roof function g is
 $C^{\infty }$
. The function f is
$C^{\infty }$
. The function f is
 $C^1$
, and for any desired k, it can be made
$C^1$
, and for any desired k, it can be made
 $C^k$
by increasing the dimension m; this means that the same is true of the map S.
$C^k$
by increasing the dimension m; this means that the same is true of the map S.
The second fact may be of interest since the authors of [Reference Kanigowski, Lemańczyk and Radziwiłł4] prove a positive result for convergence along prime iterates of similar skew products
![]() $(x, y) \mapsto (x+\alpha , y+f(x))$
under the assumption that the function f is real analytic and provide some counterexamples with continuous f. Though the constructions are not exactly the same, and though the primes absolutely do not satisfy the assumption of Theorem 1.3, in some sense, fact (2) suggests that no
$(x, y) \mapsto (x+\alpha , y+f(x))$
under the assumption that the function f is real analytic and provide some counterexamples with continuous f. Though the constructions are not exactly the same, and though the primes absolutely do not satisfy the assumption of Theorem 1.3, in some sense, fact (2) suggests that no
![]() $C^k$
condition is sufficient for good averaging of skew products along sparse sequences.
$C^k$
condition is sufficient for good averaging of skew products along sparse sequences.
We note that Theorem 1.3 clearly applies to any sequence
![]() $w_n = p(n)$
for a non-constant polynomial
$w_n = p(n)$
for a non-constant polynomial
![]() $p: \mathbb {N} \rightarrow \mathbb {N}_0$
(possibly omitting finitely many terms), and so, by simply defining
$p: \mathbb {N} \rightarrow \mathbb {N}_0$
(possibly omitting finitely many terms), and so, by simply defining
![]() $z_n$
to be
$z_n$
to be
![]() $\tfrac 12$
when
$\tfrac 12$
when
![]() $\mu (n) = 1$
and
$\mu (n) = 1$
and
![]() $0$
otherwise, one achieves
$0$
otherwise, one achieves
 $$ \begin{align*} \frac{1}{N} \sum_{n=1}^N \mu(n) \pi(S^{p(n)} \textbf{0}) = \frac{0.5 |\mu^{-1}(\{1\}) \cap \{1, \ldots, N\}|}{N}, \end{align*} $$
$$ \begin{align*} \frac{1}{N} \sum_{n=1}^N \mu(n) \pi(S^{p(n)} \textbf{0}) = \frac{0.5 |\mu^{-1}(\{1\}) \cap \{1, \ldots, N\}|}{N}, \end{align*} $$
which does not approach
![]() $0$
as
$0$
as
![]() $N \rightarrow \infty $
, disproving the polynomial Sarnak conjecture for every non-constant p. The same is true of any function p with polynomial growth, even for degree less than
$N \rightarrow \infty $
, disproving the polynomial Sarnak conjecture for every non-constant p. The same is true of any function p with polynomial growth, even for degree less than
![]() $2$
, e.g.
$2$
, e.g.
![]() $p(n) = \lfloor n^{1.01} \rfloor $
. Theorem 1.3 cannot be applied to more slowly growing p such as
$p(n) = \lfloor n^{1.01} \rfloor $
. Theorem 1.3 cannot be applied to more slowly growing p such as
![]() $\lfloor n \ln n \rfloor $
. However, the author proved a different result in [Reference Pavlov7] using subshifts, which applies to all sequences of zero Banach density. (A subshift is a closed shift-invariant subset of
$\lfloor n \ln n \rfloor $
. However, the author proved a different result in [Reference Pavlov7] using subshifts, which applies to all sequences of zero Banach density. (A subshift is a closed shift-invariant subset of
![]() $A^{\mathbb {Z}}$
(for some finite alphabet A) endowed with the left-shift transformation.)
$A^{\mathbb {Z}}$
(for some finite alphabet A) endowed with the left-shift transformation.)
Specifically, [Reference Pavlov7, Corollary 3.1] states that for any sequence of zero Banach density (regardless of growth rate), there exists a minimal subshift whose points can achieve arbitrary behavior along that sequence. However, entropy was not mentioned there, and although the proof there can indeed yield a zero entropy subshift, it is not easy to verify; the construction is quite complicated to achieve
![]() $(X,T)$
which is totally minimal, totally uniquely ergodic, and topologically mixing.
$(X,T)$
which is totally minimal, totally uniquely ergodic, and topologically mixing.
In this note, we present a streamlined self-contained proof of the following result, which shows that minimal zero entropy subshifts can realize arbitrary behavior along any sequence of zero Banach density.
Theorem 1.5. For any
![]() $S = \{s_1, s_2, \ldots \} \subset \mathbb {N}$
with
$S = \{s_1, s_2, \ldots \} \subset \mathbb {N}$
with
![]() $d^*(S) = 0$
and any finite alphabet A, there exists a minimal zero entropy subshift
$d^*(S) = 0$
and any finite alphabet A, there exists a minimal zero entropy subshift
![]() $X \subset A^{\mathbb {Z}}$
so that for every
$X \subset A^{\mathbb {Z}}$
so that for every
![]() $u \in A^{\mathbb {N}}$
, there is
$u \in A^{\mathbb {N}}$
, there is
![]() $x_u \in X$
where
$x_u \in X$
where
![]() $x_u(s_n) = u(n)$
for all
$x_u(s_n) = u(n)$
for all
![]() $s \in S$
.
$s \in S$
.
We note that this proves that even with substantially weaker hypotheses, nothing in the spirit of the polynomial Sarnak conjecture can hold under only the assumptions of minimality and zero entropy. Even if p is only assumed to have a range of zero Banach density and
![]() $\rho : \mathbb {N} \rightarrow \mathbb {Z}$
is only assumed to have
$\rho : \mathbb {N} \rightarrow \mathbb {Z}$
is only assumed to have
![]() $\limsup\ ({1}/{N}) \sum _{n=1}^N |\rho (n)|> 0$
(equivalently,
$\limsup\ ({1}/{N}) \sum _{n=1}^N |\rho (n)|> 0$
(equivalently,
![]() $\rho $
takes non-zero values on a set of positive upper density), one can define a subshift X on
$\rho $
takes non-zero values on a set of positive upper density), one can define a subshift X on
![]() $\{-1,0,1\}$
and
$\{-1,0,1\}$
and
![]() $x_u \in X$
as in Theorem 1.5 for
$x_u \in X$
as in Theorem 1.5 for
![]() $u(n) = \textrm {sgn}(\rho (n))$
. Then, for
$u(n) = \textrm {sgn}(\rho (n))$
. Then, for
![]() $f \in C(X)$
defined by
$f \in C(X)$
defined by
![]() $x \mapsto x(0)$
, the limit supremum of the averages
$x \mapsto x(0)$
, the limit supremum of the averages
 $$ \begin{align*} \frac{1}{N} \sum_{n=1}^N \rho(n) f(\sigma^{p(n)} x_u) &=\frac{1}{N} \sum_{n=1}^N \rho(n) x_u(p(n)) = \frac{1}{N} \sum_{n=1}^N \rho(n) u(n)\\ &= \frac{1}{N} \sum_{n=1}^N \rho(n) \textrm{sgn}(\rho(n)) =\frac{1}{N} \sum_{n=1}^N |\rho(n)| \end{align*} $$
$$ \begin{align*} \frac{1}{N} \sum_{n=1}^N \rho(n) f(\sigma^{p(n)} x_u) &=\frac{1}{N} \sum_{n=1}^N \rho(n) x_u(p(n)) = \frac{1}{N} \sum_{n=1}^N \rho(n) u(n)\\ &= \frac{1}{N} \sum_{n=1}^N \rho(n) \textrm{sgn}(\rho(n)) =\frac{1}{N} \sum_{n=1}^N |\rho(n)| \end{align*} $$
is positive by assumption.
We note that when
![]() $\rho = \mu $
is the Möbius function, this means that
$\rho = \mu $
is the Möbius function, this means that
 $$ \begin{align*} \frac{1}{N} \sum_{n=1}^N \mu(n) f(\sigma^{p(n)} x_u) \end{align*} $$
$$ \begin{align*} \frac{1}{N} \sum_{n=1}^N \mu(n) f(\sigma^{p(n)} x_u) \end{align*} $$
can be made to approach
![]() ${6}/{\pi ^2}$
(for
${6}/{\pi ^2}$
(for
![]() $x_u$
in a minimal zero-entropy subshift), a slight improvement of [Reference Lian and Shi6] which showed that it could attain values arbitrarily close to
$x_u$
in a minimal zero-entropy subshift), a slight improvement of [Reference Lian and Shi6] which showed that it could attain values arbitrarily close to
![]() ${6}/{\pi ^2}$
.
${6}/{\pi ^2}$
.
Remark 1.6. The phenomenon of a subshift achieving arbitrary values along a sequence is closely related to the notion of interpolation sets defined in [Reference Glasner and Weiss2]; see [Reference Koutsogiannis, Le, Moreira, Pavlov and Richter5] for a recent survey.
2. Definitions
A topological dynamical system
![]() $(X, T)$
is defined by a compact metric space X and homeomorphism
$(X, T)$
is defined by a compact metric space X and homeomorphism
![]() $T: X \rightarrow X$
. A subshift is a topological dynamical system defined by some finite set A (called the alphabet) and the restriction of the left shift map
$T: X \rightarrow X$
. A subshift is a topological dynamical system defined by some finite set A (called the alphabet) and the restriction of the left shift map
![]() $\sigma : A^{\mathbb {Z}} \rightarrow A^{\mathbb {Z}}$
defined by
$\sigma : A^{\mathbb {Z}} \rightarrow A^{\mathbb {Z}}$
defined by
![]() $(\sigma x)(n) = x(n+1)$
to some closed and
$(\sigma x)(n) = x(n+1)$
to some closed and
![]() $\sigma $
-invariant
$\sigma $
-invariant
![]() $X \subset A^{\mathbb {Z}}$
(with the induced product topology). A subshift
$X \subset A^{\mathbb {Z}}$
(with the induced product topology). A subshift
![]() $(X, \sigma )$
is minimal if for every
$(X, \sigma )$
is minimal if for every
![]() $x \in X$
,
$x \in X$
,
![]() $\{\sigma ^n x\}_{n \in \mathbb {Z}}$
is dense in X.
$\{\sigma ^n x\}_{n \in \mathbb {Z}}$
is dense in X.
A word over A is any finite string of symbols from A; a word
![]() $w = w(1) \cdots w(n)$
is said to be a subword of a word or infinite sequence x if there exists i so that
$w = w(1) \cdots w(n)$
is said to be a subword of a word or infinite sequence x if there exists i so that
![]() $w(1) \cdots w(n) = x(i+1) \cdots x(i+n)$
. The language
$w(1) \cdots w(n) = x(i+1) \cdots x(i+n)$
. The language
![]() $L(X)$
of a subshift
$L(X)$
of a subshift
![]() $(X, \sigma )$
is the set of all subwords of sequences in X, and for any
$(X, \sigma )$
is the set of all subwords of sequences in X, and for any
![]() $n \in \mathbb {N}$
, we denote
$n \in \mathbb {N}$
, we denote
![]() $L_n(X) = L(X) \cap A^n$
. For two words
$L_n(X) = L(X) \cap A^n$
. For two words
![]() $u = u(1) \cdots u(m)$
and
$u = u(1) \cdots u(m)$
and
![]() $v = v(1) \cdots v(n)$
, denote by
$v = v(1) \cdots v(n)$
, denote by
![]() $uv$
their concatenation
$uv$
their concatenation
![]() $u(1) \cdots u(m) v(1) \cdots v(n)$
.
$u(1) \cdots u(m) v(1) \cdots v(n)$
.
We do not give a full definition of topological entropy here, but note that it is a number
![]() $h(X,T) \in [0, \infty ]$
associated to any TDS
$h(X,T) \in [0, \infty ]$
associated to any TDS
![]() $(X, T)$
which is conjugacy-invariant. We will only need the following definition for subshifts: for any
$(X, T)$
which is conjugacy-invariant. We will only need the following definition for subshifts: for any
![]() $(X, \sigma )$
,
$(X, \sigma )$
,
The Banach density of a set
![]() $S \subset \mathbb {N}$
is
$S \subset \mathbb {N}$
is
3. Proof of Theorem 1.5
Proof. As in [Reference Pavlov7], we adapt the block-concatenation construction of Hahn and Katznelson [Reference Hahn and Katznelson3].
We construct X iteratively via auxiliary sequences
![]() $m_k$
of odd positive integers,
$m_k$
of odd positive integers,
![]() $A_k \subset A^{m_k}$
, and
$A_k \subset A^{m_k}$
, and
![]() $w_k \in A_k$
. Define
$w_k \in A_k$
. Define
![]() $m_0 = 1$
,
$m_0 = 1$
,
![]() $A_0 = A$
, and
$A_0 = A$
, and
![]() $w_0 = 0$
(which we assume without loss of generality to be in A). Now, suppose that
$w_0 = 0$
(which we assume without loss of generality to be in A). Now, suppose that
![]() $m_k$
,
$m_k$
,
![]() $A_k$
, and
$A_k$
, and
![]() $w_k$
are defined. Define
$w_k$
are defined. Define
![]() $m_{k+1}> \max (3m_k |A_k|, 12(\ln 2)(4/3)^{k+1})$
to be an odd multiple of
$m_{k+1}> \max (3m_k |A_k|, 12(\ln 2)(4/3)^{k+1})$
to be an odd multiple of
![]() $3m_k$
large enough that
$3m_k$
large enough that
![]() $|S \cap I|/|I| < (3m_k)^{-1}$
for all intervals I of length
$|S \cap I|/|I| < (3m_k)^{-1}$
for all intervals I of length
![]() $m_{k+1}$
(using the fact that
$m_{k+1}$
(using the fact that
![]() $d^*(S)\! = 0$
). Define
$d^*(S)\! = 0$
). Define
![]() $A_{k+1}$
to be the set of all concatenations of
$A_{k+1}$
to be the set of all concatenations of
![]() ${m_{k+1}}/{m_k}$
words in
${m_{k+1}}/{m_k}$
words in
![]() $A_k$
in which every word in
$A_k$
in which every word in
![]() $A_k$
is used at least once and in which at least one-third of the concatenated words are equal to
$A_k$
is used at least once and in which at least one-third of the concatenated words are equal to
![]() $w_k$
. Define
$w_k$
. Define
![]() $Y_k$
to be the set of shifts of biinfinite (unrestricted) concatenations of words in
$Y_k$
to be the set of shifts of biinfinite (unrestricted) concatenations of words in
![]() $A_k$
, define
$A_k$
, define
![]() $Y = \bigcap _k Y_k$
, and define X to be the subshift of Y consisting of sequences in which every subword is a subword of some
$Y = \bigcap _k Y_k$
, and define X to be the subshift of Y consisting of sequences in which every subword is a subword of some
![]() $w_k$
.
$w_k$
.
We claim that
![]() $(X, \sigma )$
is minimal. Indeed, consider any
$(X, \sigma )$
is minimal. Indeed, consider any
![]() $x \in X$
and
$x \in X$
and
![]() $w \in L(X)$
. By definition, w is a subword of
$w \in L(X)$
. By definition, w is a subword of
![]() $w_k$
for some k. By definition,
$w_k$
for some k. By definition,
![]() $w_k$
is a subword of every word in
$w_k$
is a subword of every word in
![]() $A_{k+1}$
. Finally, x is a shift of a concatenation of words in
$A_{k+1}$
. Finally, x is a shift of a concatenation of words in
![]() $A_{k+1}$
, each of which contains
$A_{k+1}$
, each of which contains
![]() $w_k$
and therefore w. So, x contains w, and since
$w_k$
and therefore w. So, x contains w, and since
![]() $w \in L(X)$
was arbitrary, the orbit of x is dense. Since
$w \in L(X)$
was arbitrary, the orbit of x is dense. Since
![]() $x \in X$
was arbitrary,
$x \in X$
was arbitrary,
![]() $(X, \sigma )$
is minimal.
$(X, \sigma )$
is minimal.
We also claim that
![]() $(X, \sigma )$
has zero entropy. We see this by bounding
$(X, \sigma )$
has zero entropy. We see this by bounding
![]() $|A_k|$
from above. For every k, each word in
$|A_k|$
from above. For every k, each word in
![]() $A_{k+1}$
is defined by an ordered
$A_{k+1}$
is defined by an ordered
![]() $(m_{k+1}/m_k)$
-tuple of words in
$(m_{k+1}/m_k)$
-tuple of words in
![]() $A_k$
, where at least one-third are
$A_k$
, where at least one-third are
![]() $w_k$
. The number of such tuples can be bounded from above by
$w_k$
. The number of such tuples can be bounded from above by
 $$ \begin{align*} {m_{k+1}/m_k \choose m_{k+1}/3m_k} |A_k|^{2m_{k+1}/3m_k} \leq 2^{m_{k+1}/m_k} |A_k|^{2m_{k+1}/3m_k}. \end{align*} $$
$$ \begin{align*} {m_{k+1}/m_k \choose m_{k+1}/3m_k} |A_k|^{2m_{k+1}/3m_k} \leq 2^{m_{k+1}/m_k} |A_k|^{2m_{k+1}/3m_k}. \end{align*} $$
Therefore,
Now, it is easily checked that
![]() $({\ln |A_k|})/{m_k} \leq \ln |A| (3/4)^k$
for all k by induction. The base case
$({\ln |A_k|})/{m_k} \leq \ln |A| (3/4)^k$
for all k by induction. The base case
![]() $k = 0$
is immediate. For the inductive step, if we assume that
$k = 0$
is immediate. For the inductive step, if we assume that
![]() $({\ln |A_k|})/{m_k} \leq \ln |A| (3/4)^k$
, then recalling that
$({\ln |A_k|})/{m_k} \leq \ln |A| (3/4)^k$
, then recalling that
![]() $m_k> 12(\ln 2) (4/3)^k$
,
$m_k> 12(\ln 2) (4/3)^k$
,
Therefore, for all k,
![]() $|A_k| \leq e^{\ln |A| (3/4)^k m_k}$
. Finally, we note that every word in
$|A_k| \leq e^{\ln |A| (3/4)^k m_k}$
. Finally, we note that every word in
![]() $L_{m_k}(X)$
is a subword of a concatenation of a pair of words in
$L_{m_k}(X)$
is a subword of a concatenation of a pair of words in
![]() $A_k$
, so determined by such a pair and by the location of the first letter. Therefore,
$A_k$
, so determined by such a pair and by the location of the first letter. Therefore,
![]() $|L_{m_k}(X)| \leq m_k |A_k|^2 < m_k e^{2\ln |A|(3/4)^k m_k}$
. This clearly implies that
$|L_{m_k}(X)| \leq m_k |A_k|^2 < m_k e^{2\ln |A|(3/4)^k m_k}$
. This clearly implies that
that is,
![]() $\mathbf {X}$
has zero entropy.
$\mathbf {X}$
has zero entropy.
It remains, for
![]() $u \in A^{\mathbb {N}}$
, to construct
$u \in A^{\mathbb {N}}$
, to construct
![]() $x_u \in X$
with
$x_u \in X$
with
![]() $x_u(s_n) = u(n)$
for all
$x_u(s_n) = u(n)$
for all
![]() $s_n \in S$
. The construction of
$s_n \in S$
. The construction of
![]() $x_u$
proceeds in steps, where it is continually assigned letters from A on portions of
$x_u$
proceeds in steps, where it is continually assigned letters from A on portions of
![]() $\mathbb {Z}$
, with undefined portions labeled by
$\mathbb {Z}$
, with undefined portions labeled by
![]() $*$
. Formally, define
$*$
. Formally, define
![]() $x^{(0)} \in A \sqcup \{*\}^{\mathbb {Z}}$
by
$x^{(0)} \in A \sqcup \{*\}^{\mathbb {Z}}$
by
![]() $x^{(0)}(s_n) = u(n)$
for
$x^{(0)}(s_n) = u(n)$
for
![]() $s \in S$
and
$s \in S$
and
![]() $*$
for all other locations.
$*$
for all other locations.
Now partition
![]() $\mathbb {Z}$
into the intervals
$\mathbb {Z}$
into the intervals
![]() $((i-0.5)m_1, (i+0.5)m_1)$
(herein, all intervals are assumed to be intersected with
$((i-0.5)m_1, (i+0.5)m_1)$
(herein, all intervals are assumed to be intersected with
![]() $\mathbb {Z}$
). For every i for which
$\mathbb {Z}$
). For every i for which
![]() $S \cap ((i-0.5)m_1, (i+0.5)m_1) \neq \varnothing $
, consider the
$S \cap ((i-0.5)m_1, (i+0.5)m_1) \neq \varnothing $
, consider the
![]() $m_1$
-letter word
$m_1$
-letter word
![]() $x^{(0)}(((i-0.5)m_1, (i+0.5)m_1))$
. By definition of
$x^{(0)}(((i-0.5)m_1, (i+0.5)m_1))$
. By definition of
![]() $m_1$
,
$m_1$
,
![]() $|S \cap ((i-0.5)m_1, \ldots , (i+0.5)m_1)| < m_1/3m_0 = m_1/3$
, and so at most one-third of the letters in this word are non-
$|S \cap ((i-0.5)m_1, \ldots , (i+0.5)m_1)| < m_1/3m_0 = m_1/3$
, and so at most one-third of the letters in this word are non-
![]() $*$
. Fill the remaining locations by assigning the first
$*$
. Fill the remaining locations by assigning the first
![]() $m_1/3$
as
$m_1/3$
as
![]() $w_0 = 0$
. At least
$w_0 = 0$
. At least
![]() $m_1/3$
letters remain, which is larger than
$m_1/3$
letters remain, which is larger than
![]() $|A_0| = |A|$
by definition of
$|A_0| = |A|$
by definition of
![]() $m_1$
. Fill those in an arbitrary way which uses all letters from A at least once. The resulting
$m_1$
. Fill those in an arbitrary way which uses all letters from A at least once. The resulting
![]() $m_1$
-letter word is in
$m_1$
-letter word is in
![]() $A_1$
by definition, call it
$A_1$
by definition, call it
![]() $w^{(1)}_i$
. Now, define
$w^{(1)}_i$
. Now, define
![]() $x^{(1)}$
by setting
$x^{(1)}$
by setting
![]() $x^{(1)}(((i-0.5)m_1, (i+0.5)m_1)) = w^{(1)}_i$
for all i as above (that is, those for which
$x^{(1)}(((i-0.5)m_1, (i+0.5)m_1)) = w^{(1)}_i$
for all i as above (that is, those for which
![]() $S \cap ((i-0.5)m_1, (i+0.5)m_1) \neq \varnothing $
) and
$S \cap ((i-0.5)m_1, (i+0.5)m_1) \neq \varnothing $
) and
![]() $*$
elsewhere. Note that
$*$
elsewhere. Note that
![]() $x^{(1)}$
is an infinite concatenation of words in
$x^{(1)}$
is an infinite concatenation of words in
![]() $A_1$
and blocks of
$A_1$
and blocks of
![]() $*$
of length
$*$
of length
![]() $m_1$
and that
$m_1$
and that
![]() $x^{(1)}$
contains
$x^{(1)}$
contains
![]() $*$
on any interval
$*$
on any interval
![]() $((i-0.5)m_1, (i+0.5)m_1)$
which is disjoint from S.
$((i-0.5)m_1, (i+0.5)m_1)$
which is disjoint from S.
Now, suppose that
![]() $x^{(k)}$
has been defined as an infinite concatenation of words in
$x^{(k)}$
has been defined as an infinite concatenation of words in
![]() $A_k$
and blocks of
$A_k$
and blocks of
![]() $*$
of length
$*$
of length
![]() $m_k$
which contains
$m_k$
which contains
![]() $*$
on any interval
$*$
on any interval
![]() $((i-0.5)m_k, (i+0.5)m_k)$
which is disjoint from S. We wish to extend
$((i-0.5)m_k, (i+0.5)m_k)$
which is disjoint from S. We wish to extend
![]() $x^{(k)}$
to
$x^{(k)}$
to
![]() $x^{(k+1)}$
by changing some
$x^{(k+1)}$
by changing some
![]() $*$
symbols to letters in A. Consider any i for which
$*$
symbols to letters in A. Consider any i for which
![]() $S \cap ((i-0.5)m_{k+1}, \ldots , (i+0.5)m_{k+1}) \neq \varnothing $
. The portion of
$S \cap ((i-0.5)m_{k+1}, \ldots , (i+0.5)m_{k+1}) \neq \varnothing $
. The portion of
![]() $x^{(k)}$
occupying that interval is a concatenation of words in
$x^{(k)}$
occupying that interval is a concatenation of words in
![]() $A_k$
and blocks of
$A_k$
and blocks of
![]() $*$
of length
$*$
of length
![]() $m_k$
(we use here the fact that
$m_k$
(we use here the fact that
![]() $m_{k+1}$
is odd), and the number which are words in
$m_{k+1}$
is odd), and the number which are words in
![]() $A_k$
is bounded from above by the number of
$A_k$
is bounded from above by the number of
![]() $j \in ((i-0.5)m_{k+1}/m_k, (i+0.5)m_{k+1}/m_k)$
for which
$j \in ((i-0.5)m_{k+1}/m_k, (i+0.5)m_{k+1}/m_k)$
for which
![]() $((j-0.5)m_k, (j+0.5)m_k)$
is not disjoint from S, which in turn is bounded from above by
$((j-0.5)m_k, (j+0.5)m_k)$
is not disjoint from S, which in turn is bounded from above by
![]() $|S \cap ((i-0.5)m_{k+1}, (i+0.5)m_{k+1})|$
, which by definition of
$|S \cap ((i-0.5)m_{k+1}, (i+0.5)m_{k+1})|$
, which by definition of
![]() $m_{k+1}$
is less than
$m_{k+1}$
is less than
![]() $m_{k+1}/3m_k$
. Therefore, at least two-thirds of the concatenated
$m_{k+1}/3m_k$
. Therefore, at least two-thirds of the concatenated
![]() $m_k$
-blocks comprising
$m_k$
-blocks comprising
![]() $x^{(k)}(((i-0.5)m_{k+1}, (i+0.5)m_{k+1}))$
are blocks of
$x^{(k)}(((i-0.5)m_{k+1}, (i+0.5)m_{k+1}))$
are blocks of
![]() $*$
. Fill the first
$*$
. Fill the first
![]() $m_{k+1}/3m_k$
of these with
$m_{k+1}/3m_k$
of these with
![]() $w_k$
. Then at least
$w_k$
. Then at least
![]() $m_{k+1}/3m_k$
blocks remain, which is more than
$m_{k+1}/3m_k$
blocks remain, which is more than
![]() $|A_k|$
by definition of
$|A_k|$
by definition of
![]() $m_{k+1}$
. Fill these in an arbitrary way which uses each word in
$m_{k+1}$
. Fill these in an arbitrary way which uses each word in
![]() $|A_k|$
at least once. By definition, this creates a word in
$|A_k|$
at least once. By definition, this creates a word in
![]() $A_{k+1}$
, which we denote by
$A_{k+1}$
, which we denote by
![]() $w^{(k+1)}_i$
. Define
$w^{(k+1)}_i$
. Define
![]() $x^{(k+1)}(((i-0.5)m_{k+1}, (i+0.5)m_{k+1})) = w^{(k+1)}_i$
for any i as above (that is, those for which
$x^{(k+1)}(((i-0.5)m_{k+1}, (i+0.5)m_{k+1})) = w^{(k+1)}_i$
for any i as above (that is, those for which
![]() $S \cap ((i-0.5)m_{k+1}, (i+0.5)m_{k+1}) \neq \varnothing $
) and as
$S \cap ((i-0.5)m_{k+1}, (i+0.5)m_{k+1}) \neq \varnothing $
) and as
![]() $*$
elsewhere. Note that
$*$
elsewhere. Note that
![]() $x^{(k+1)}$
is an infinite concatenation of words in
$x^{(k+1)}$
is an infinite concatenation of words in
![]() $A_{k+1}$
and blocks of
$A_{k+1}$
and blocks of
![]() $*$
of length
$*$
of length
![]() $m_{k+1}$
which contains
$m_{k+1}$
which contains
![]() $*$
on any interval
$*$
on any interval
![]() $((i-0.5)m_{k+1}, (i+0.5)m_{k+1})$
which is disjoint from S.
$((i-0.5)m_{k+1}, (i+0.5)m_{k+1})$
which is disjoint from S.
We now have defined
![]() $x^{(k)} \in (A \sqcup \{*\})^{\mathbb {Z}}$
for all
$x^{(k)} \in (A \sqcup \{*\})^{\mathbb {Z}}$
for all
![]() $k \in \mathbb {N}$
. Since each is obtained from the previous by changing some
$k \in \mathbb {N}$
. Since each is obtained from the previous by changing some
![]() $*$
symbols to letters from A, they approach a limit
$*$
symbols to letters from A, they approach a limit
![]() $x_u$
which agrees with
$x_u$
which agrees with
![]() $x^{(0)}$
on all locations where
$x^{(0)}$
on all locations where
![]() $x^{(0)}$
had letters from A, that is,
$x^{(0)}$
had letters from A, that is,
![]() $x_u(s_n) = u(n)$
for all
$x_u(s_n) = u(n)$
for all
![]() $n \in \mathbb {N}$
. Since
$n \in \mathbb {N}$
. Since
![]() $S \neq \varnothing $
,
$S \neq \varnothing $
,
![]() $S \cap (-0.5m_k, 0.5m_k) \neq \varnothing $
for all large enough k, and so
$S \cap (-0.5m_k, 0.5m_k) \neq \varnothing $
for all large enough k, and so
![]() $x^{(k)}((-0.5m_k, 0.5m_k))$
has no
$x^{(k)}((-0.5m_k, 0.5m_k))$
has no
![]() $*$
, meaning that
$*$
, meaning that
![]() $x_u \in A^{\mathbb {Z}}$
.
$x_u \in A^{\mathbb {Z}}$
.
It remains only to show that
![]() $x_u \in X$
. By definition,
$x_u \in X$
. By definition,
![]() $x_u$
is a concatenation of words in
$x_u$
is a concatenation of words in
![]() $A_k$
for every k, so
$A_k$
for every k, so
![]() $x_u \in Y = \bigcap _k Y_k$
as in the definition of X. Finally, every subword w of
$x_u \in Y = \bigcap _k Y_k$
as in the definition of X. Finally, every subword w of
![]() $x_u$
is contained in
$x_u$
is contained in
![]() $x_u((-0.5m_k, 0.5m_k))$
for large enough k, and this word is in
$x_u((-0.5m_k, 0.5m_k))$
for large enough k, and this word is in
![]() $A_k$
by definition. Since all words in
$A_k$
by definition. Since all words in
![]() $A_k$
are subwords of
$A_k$
are subwords of
![]() $w_{k+1}$
, w is also. Therefore, by definition,
$w_{k+1}$
, w is also. Therefore, by definition,
![]() ${x_u \in X}$
and
${x_u \in X}$
and
![]() ${x_u(s_n) = u(n)}$
for all n, completing the proof.
${x_u(s_n) = u(n)}$
for all n, completing the proof.
Remark 3.1. We observe that the assumption of zero Banach density cannot be weakened in Theorem 1.5. Assume for a contradiction that
![]() $S \subset \mathbb {N}$
has
$S \subset \mathbb {N}$
has
![]() $d^*(S) = \alpha> 0$
, and that every
$d^*(S) = \alpha> 0$
, and that every
![]() $u \in A^{\mathbb {N}}$
could be assigned
$u \in A^{\mathbb {N}}$
could be assigned
![]() $x_u$
as in Theorem 1.5. By definition of Banach density, there exist intervals
$x_u$
as in Theorem 1.5. By definition of Banach density, there exist intervals
![]() $I_n$
with lengths approaching infinity so that
$I_n$
with lengths approaching infinity so that
![]() $|S \cap I_n|/|I_n|> \alpha /2$
for all n. For every n, since all possible assignments of letters from A to locations in
$|S \cap I_n|/|I_n|> \alpha /2$
for all n. For every n, since all possible assignments of letters from A to locations in
![]() $S \cap I_n$
give rise to sequences in X,
$S \cap I_n$
give rise to sequences in X,
![]() $|L_{|I_n|}(X)| \geq 2^{|S \cap I_n|}> |A|^{\alpha |I_n|/2}$
. Then,
$|L_{|I_n|}(X)| \geq 2^{|S \cap I_n|}> |A|^{\alpha |I_n|/2}$
. Then,
 $$ \begin{align*} h(X) = \lim_n \frac{\ln |L_{|I_n|}(X)|}{|I_n|} \geq \limsup \frac{\ln |A|^{\alpha|I_n|/2}}{|I_n|} = \alpha (\ln |A|)/2> 0. \end{align*} $$
$$ \begin{align*} h(X) = \lim_n \frac{\ln |L_{|I_n|}(X)|}{|I_n|} \geq \limsup \frac{\ln |A|^{\alpha|I_n|/2}}{|I_n|} = \alpha (\ln |A|)/2> 0. \end{align*} $$
Therefore, no such X, minimal or otherwise, can have zero entropy.
Acknowledgements
The author gratefully acknowledges the support of a Simons Foundation Collaboration Grant. The author would like to thank his PhD advisor, Vitaly Bergelson, for introducing him to this problem, and would also like to thank Anh Le for bringing the connection to the polynomial Sarnak conjecture to his attention.