Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-29T03:05:13.427Z Has data issue: false hasContentIssue false
  • English
  • Français

A minimal subsystem of the Kari–Culik tilings

Published online by Cambridge University Press:  11 February 2016

JASON SIEFKEN
JASON SIEFKEN*
Affiliation:
Department of Mathematics, Northwestern University, 2033 Sheridan Road, Evanston, IL 60208, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The Kari–Culik tilings are formed from a set of 13 Wang tiles that tile the plane only aperiodically. They are the smallest known set of Wang tiles to do so and are not as well understood as other examples of aperiodic Wang tiles. We show that the 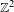$\mathbb{Z}^{2}$ action by translation on a certain subset of the Kari–Culik tilings, namely those whose rows can be interpreted as Sturmian sequences (rotation sequences), is minimal. We give a characterization of this space as a skew product as well as explicit bounds on the waiting time between occurrences of $m\times n$ configurations.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 37 , Issue 5 , August 2017 , pp. 1607 - 1634
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berenstein, C. A. and Lavine, D.. On the number of digital straight line segments. IEEE Trans. Pattern Anal. Mach. Intell. 10(6) (1988), 880–887.CrossRefGoogle Scholar
Durand, B., Gamard, G. and Grandjean, A.. Aperiodic tilings and entropy. 18th Int. Conf. Developments in Language Theory, DLT 2014 (Ekaterinburg, Russia, 2014) (Lecture Notes in Computer Science, 8688) . Eds. Shur, A. M. and Volkov, M. V.. Springer International, Switzerland, 2014, pp. 166–177.Google Scholar
Eigen, S., Navarro, J. and Prasad, V. S.. An aperiodic tiling using a dynamical system and Beatty sequences. Dynamics, Ergodic Theory, and Geometry (Mathematical Sciences Research Institute Publications, 54) . Cambridge University Press, Cambridge, 2007, pp. 223–241.CrossRefGoogle Scholar
Fogg, N. P.. Substitutions in Dynamics, Arithmetics and Combinatorics (Lecture Notes in Mathematics, 1794) . Eds. Berthé, V., Ferenczi, S., Mauduit, C. and Siegel, A.. Springer, Berlin, 2002.CrossRefGoogle Scholar
Liousse, I.. PL homeomorphisms of the circle which are piecewise C 1 conjugate to irrational rotations. Bull. Braz. Math. Soc. (N.S.) 35(2) (2004), 269–280.CrossRefGoogle Scholar
Lothaire, M.. Algebraic Combinatorics on Words (Encyclopedia of Mathematics and its Applications, 90) . Cambridge University Press, Cambridge, 2002, A collective work by J. Berstel, D. Perrin, P. Seebold, J. Cassaigne, A. De Luca, S. Varricchio, A. Lascoux, B. Leclerc, J.-Y. Thibon, V. Bruyere, C. Frougny, F. Mignosi, A. Restivo, C. Reutenauer, D. Foata, G.-N. Han, J. Desarmenien, V. Diekert, T. Harju, J. Karhumaki, and W. Plandowski, with a preface by Berstel and Perrin.Google Scholar
Rhin, G.. Approximants de Padé et mesures effectives d’irrationalité. Séminaire de Théorie des Nombres, Paris 1985–86 (Progress in Mathematics, 71) . Birkhäuser, Boston, MA, 1987, pp. 155–164.CrossRefGoogle Scholar
Robinson, E. A. Jr. The tilings of Kari and Culik. Numeration: Mathematics and Computer Science (CIRM, Marseilles, 2009). Unpublished conference talk available at http://home.gwu.edu/∼robinson/Documents/Marseille.pdf.Google Scholar