Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-27T05:08:32.675Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal convergence on Lp spaces

Published online by Cambridge University Press:  19 September 2008

I. Assani
I. Assani
Affiliation:
Department of Mathematics, University of Toronto, Ontario, Canada, M5S 1A1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let (X, F, μ) be a probability measure space, p and β real numbers such that 1≤p<+∞ and 0<β<p. For any linear positive operator T satisfying T1, T*1 = 1 we prove the norm and pointwise convergence of the sequence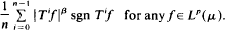 We get then the pointwise and norm convergence in Lp, 0 < β ≥ 1 < p < 2, of the sequence 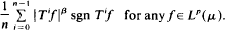sgn Sif for any positive linear operator on Lp(Ω, A, μ) (μ-σ-finite) verifying ∥(1 − α)I + αS∥p ≤ 1 for a real number 0 < α < 1. In the particular case α = 1, (S is a contraction), β = p−l, this result gives the pointwise and norm convergence of the sequences introduced by Beauzamy and Enflo in 1985 to the asymptotic center of the sequence .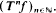

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 10 , Issue 3 , September 1990 , pp. 411 - 420
Copyright
Copyright © Cambridge University Press 1990

References

REFERENCES

[1]Assani, I.. Estimates of positive linear operators in L p. Proc. Amer. Math. Soc. accepted.Google Scholar
[2]Beauzamy, B. & Enflo, P.. Théorèmes de points fixes et d'approximation. Arkiv Math. 23 (1985), 19–34.CrossRefGoogle Scholar
[3]Benozene, R.. Sommes minimales des itérés d'une contraction dans les espaces de Hilbert et de Banach. Thèse de 3eme cycle, Université Pierre et Marie Curie, 29 Octobre 1981.Google Scholar
[4]Bruck, R. E. & Reich, S.. Accretive operators, Banach limits, and dual ergodic theorems. Bull. de l'Acad. Polon. des Sciences 19 Nos. 11–12 (1981), 585–589.Google Scholar
[5]Derriennic, Y.. Un théorème ergodique presque sous additif. Ann. of Prob. 11, 669–677.Google Scholar
[6]Edelstein, M.. The construction of an asymptotic center with a fixed point property. Bull. Amer. Math. Soc. 78 (1972), 206–208.CrossRefGoogle Scholar
[7]Guerre, S.. Procédé de convergence minimale dans les espaces de Banach. Une loi des grands nombres et un théorème ergodique. Sem. Geom. Espaces de Banach, Ec. polytech., Cent. Math (1977–1978), Exposé, 1–14.Google Scholar
[8]Krengel, U.. Ergodic theorems. Studies in Mathematics, de Gruyter, 1985.Google Scholar