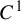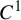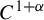1 Introduction
Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{1+\alpha }$
expanding map on a compact smooth Riemannian manifold M with a conformal repeller
$C^{1+\alpha }$
expanding map on a compact smooth Riemannian manifold M with a conformal repeller
![]() $\Lambda $
. Let
$\Lambda $
. Let
![]() $\mu $
be the unique equilibrium measure corresponding to the Hölder continuous function
$\mu $
be the unique equilibrium measure corresponding to the Hölder continuous function
![]() $-s\log \|D_xf\|$
, where s is the unique solution of Bowen’s equation
$-s\log \|D_xf\|$
, where s is the unique solution of Bowen’s equation
then the following properties hold:
-
(1)
 $\dim _H \Lambda =\dim _B\Lambda =s$
;
$\dim _H \Lambda =\dim _B\Lambda =s$
; -
(2) the s-Hausdorff dimension of
 $\Lambda $
is positive and finite, moreover, it is equivalent to the equilibrium measure
$\Lambda $
is positive and finite, moreover, it is equivalent to the equilibrium measure
 $\mu $
;
$\mu $
; -
(3)
 $\dim _H\mu =\dim _H\Lambda $
,
$\dim _H\mu =\dim _H\Lambda $
,
where
![]() ${\dim _H}$
and
${\dim _H}$
and
![]() $\dim _B$
denote the Hausdorff dimension and the box dimension, respectively. The first property of Hausdorff dimension was first established by Bowen in a special case [Reference Bowen8]. Ruelle showed the general case in [Reference Ruelle24], where his proof consists of showing the second property. Falconer [Reference Falconer15] obtained the equality between Hausdorff dimension and box dimension. Later, the smoothness
$\dim _B$
denote the Hausdorff dimension and the box dimension, respectively. The first property of Hausdorff dimension was first established by Bowen in a special case [Reference Bowen8]. Ruelle showed the general case in [Reference Ruelle24], where his proof consists of showing the second property. Falconer [Reference Falconer15] obtained the equality between Hausdorff dimension and box dimension. Later, the smoothness
![]() $C^{1+\alpha }$
was eventually relaxed to
$C^{1+\alpha }$
was eventually relaxed to
![]() $C^1$
by Gatzouras and Peres [Reference Gatzouras and Peres18]. The third property is clear from the variational principle of topological pressure. Such a measure is called the measure of full dimension.
$C^1$
by Gatzouras and Peres [Reference Gatzouras and Peres18]. The third property is clear from the variational principle of topological pressure. Such a measure is called the measure of full dimension.
By the variational principle of topological pressure, there exists an equilibrium measure provided that the entropy map
![]() $\mu \mapsto h_\mu (f)$
is upper semi-continuous. The existence of measures of full dimension could be regarded as a dimensional version of the existence of an equilibrium state. However, the map
$\mu \mapsto h_\mu (f)$
is upper semi-continuous. The existence of measures of full dimension could be regarded as a dimensional version of the existence of an equilibrium state. However, the map
![]() $\mu \mapsto \dim _H\mu $
enjoys no continuity property even if the entropy map is upper semi-continuous. This is the crucial difference between dimension and pressure/entropy.
$\mu \mapsto \dim _H\mu $
enjoys no continuity property even if the entropy map is upper semi-continuous. This is the crucial difference between dimension and pressure/entropy.
As one can see, a
![]() $C^1$
conformal repeller admits a measure of full dimension. How about the non-conformal and hyperbolic case? The answer is usually negative, although a certain special non-conformal repeller–average conformal repeller, which is introduced in [Reference Ban, Cao and Hu2], does have an ergodic measure of full dimension (see [Reference Cao, Hu and Zhao10, Theorem E]). So it is natural to generalize the question into two parts: one is to consider a general quantity of dimension type; the other one is to consider the existence of measures of maximal dimension, that is, try to find an invariant measure which attains the supremum of the following quantity:
$C^1$
conformal repeller admits a measure of full dimension. How about the non-conformal and hyperbolic case? The answer is usually negative, although a certain special non-conformal repeller–average conformal repeller, which is introduced in [Reference Ban, Cao and Hu2], does have an ergodic measure of full dimension (see [Reference Cao, Hu and Zhao10, Theorem E]). So it is natural to generalize the question into two parts: one is to consider a general quantity of dimension type; the other one is to consider the existence of measures of maximal dimension, that is, try to find an invariant measure which attains the supremum of the following quantity:
This quantity was introduced by Denker and Urbański [Reference Denker and Urbański14] in the context of one-dimensional complex dynamics, where they considered the supremum over the ergodic measures of positive entropy. Later, this quantity has been intensively studied in one-dimensional complex dynamics (see [Reference Urbański25] for more details).
For non-conformal repellers, we consider a substitute quantity of dimension type called Carathéodory singular dimension (see §2.3.2 for a detailed definition) which was introduced by Cao, Pesin, and Zhao [Reference Cao, Pesin and Zhao11]. They proved its continuity for
![]() $C^{1+\alpha }$
maps under
$C^{1+\alpha }$
maps under
![]() $C^1$
topology. Later, following the approach described in [Reference Pesin21], the authors introduced the Carathéodory singular dimension of invariant measures in [Reference Cao, Wang and Zhao12], and proved that the unique zero of the measure theoretic pressure function equals the Carathéodory singular dimension of ergodic measures. For a general
$C^1$
topology. Later, following the approach described in [Reference Pesin21], the authors introduced the Carathéodory singular dimension of invariant measures in [Reference Cao, Wang and Zhao12], and proved that the unique zero of the measure theoretic pressure function equals the Carathéodory singular dimension of ergodic measures. For a general
![]() $C^1$
non-conformal repeller, in this paper, we will prove that there exists an ergodic measure of full Carathéodory singular dimension.
$C^1$
non-conformal repeller, in this paper, we will prove that there exists an ergodic measure of full Carathéodory singular dimension.
For the existence of measures of maximal dimension for hyperbolic diffeomorphisms, it was shown by Barreira and Wolf [Reference Barreira and Wolf5] that if
![]() $f: M\to M$
is a
$f: M\to M$
is a
![]() $C^{1+\alpha }$
surface diffeomorphism and
$C^{1+\alpha }$
surface diffeomorphism and
![]() $\Lambda $
is a topological mixing locally maximal hyperbolic set, then there exists an ergodic measure of maximal dimension, see [Reference Barreira4, Ch. 5] for the hyperbolic conformal case. In [Reference Rams22], Rams proved the existence of a measure of maximal dimension for piecewise linear horseshoe maps by computing
$\Lambda $
is a topological mixing locally maximal hyperbolic set, then there exists an ergodic measure of maximal dimension, see [Reference Barreira4, Ch. 5] for the hyperbolic conformal case. In [Reference Rams22], Rams proved the existence of a measure of maximal dimension for piecewise linear horseshoe maps by computing
![]() $\delta (f)$
explicitly. In [Reference Wolf30], Wolf showed that there exist finitely many measures of maximal dimension for polynomial automorphisms of
$\delta (f)$
explicitly. In [Reference Wolf30], Wolf showed that there exist finitely many measures of maximal dimension for polynomial automorphisms of
![]() $C^2$
. However, these are not guaranteed to be measures of full dimension unless the automorphism is volume preserving. It should be noted that only a minimal lack of hyperbolicity may yield no measure of maximal dimension. Urbański and Wolf [Reference Urbański and Wolf26] constructed nonlinear horseshoes of a surface, which are hyperbolic except at one parabolic fixed point, and which do not have any measure of maximal dimension.
$C^2$
. However, these are not guaranteed to be measures of full dimension unless the automorphism is volume preserving. It should be noted that only a minimal lack of hyperbolicity may yield no measure of maximal dimension. Urbański and Wolf [Reference Urbański and Wolf26] constructed nonlinear horseshoes of a surface, which are hyperbolic except at one parabolic fixed point, and which do not have any measure of maximal dimension.
For an average conformal hyperbolic (ACH for short) set
![]() $\Lambda $
of a
$\Lambda $
of a
![]() $C^{1}$
diffeomorphism, which is introduced in [Reference Wang, Wang, Cao and Zhao29], we construct a Borel probability measure
$C^{1}$
diffeomorphism, which is introduced in [Reference Wang, Wang, Cao and Zhao29], we construct a Borel probability measure
![]() $\mu $
(not necessarily invariant) on
$\mu $
(not necessarily invariant) on
![]() $\Lambda $
and show that this measure has full Hausdorff dimension, that is,
$\Lambda $
and show that this measure has full Hausdorff dimension, that is,
![]() $\dim _H\mu =\dim _H\Lambda $
. Our method consists of using the weak Gibbs measure of a continuous function. The desired measure is the product of two weak Gibbs measure with respect to the future and past behavior of the derivative continuous function along unstable and stable directions. The measure constructed in this way has support strictly inside the repeller. If
$\dim _H\mu =\dim _H\Lambda $
. Our method consists of using the weak Gibbs measure of a continuous function. The desired measure is the product of two weak Gibbs measure with respect to the future and past behavior of the derivative continuous function along unstable and stable directions. The measure constructed in this way has support strictly inside the repeller. If
![]() $\Lambda $
is an average conformal hyperbolic set of a
$\Lambda $
is an average conformal hyperbolic set of a
![]() $C^{1+\alpha }$
diffeomorphism, following Barreira and Wolf’s approach in [Reference Barreira and Wolf5], this paper proves that there exists an ergodic measure of maximal dimension, which extends the result [Reference Barreira and Wolf5] for average conformal hyperbolic sets.
$C^{1+\alpha }$
diffeomorphism, following Barreira and Wolf’s approach in [Reference Barreira and Wolf5], this paper proves that there exists an ergodic measure of maximal dimension, which extends the result [Reference Barreira and Wolf5] for average conformal hyperbolic sets.
The paper is organized as follows. In §2, we recall some necessary concepts, such as average conformal hyperbolic set and Carathéodory singular dimension, and give the statement of the main result in this paper. Section 3 presents the detailed proofs of the results in the previous section. Namely, we prove that there exists an ergodic measure of full Carathéodory singular dimension on a
![]() $C^1$
non-conformal repeller; and we construct a Borel probability measure of full Hausdorff dimension on a
$C^1$
non-conformal repeller; and we construct a Borel probability measure of full Hausdorff dimension on a
![]() $C^1$
average conformal hyperbolic set; finally, we show that there exists an ergodic measure of maximal dimension on a
$C^1$
average conformal hyperbolic set; finally, we show that there exists an ergodic measure of maximal dimension on a
![]() $C^{1+\alpha }$
average conformal hyperbolic set.
$C^{1+\alpha }$
average conformal hyperbolic set.
2 Preliminaries and statements
In this section, we recall some notions in dimension theory and smooth dynamical systems, and give the statement of the main results in this paper. The proofs will be postponed to the next section.
2.1 Topological pressure
Let
![]() $f: X\to X$
be a continuous transformation on a compact metric space X equipped with metric d. A subset
$f: X\to X$
be a continuous transformation on a compact metric space X equipped with metric d. A subset
![]() $F\subset X$
is called an
$F\subset X$
is called an
![]() $(n, \epsilon )-$
separated set with respect to f if for any two different points
$(n, \epsilon )-$
separated set with respect to f if for any two different points
![]() $x,y\in F$
, we have
$x,y\in F$
, we have
![]() $d_n(x,y):=\max _{0\leq k\leq n-1}d(f^k(x), f^k(y))>\epsilon .$
A sequence of continuous functions
$d_n(x,y):=\max _{0\leq k\leq n-1}d(f^k(x), f^k(y))>\epsilon .$
A sequence of continuous functions
![]() $\Phi =\{\phi _n\}_{n\ge 1}$
is called sub-additive, if
$\Phi =\{\phi _n\}_{n\ge 1}$
is called sub-additive, if
Given a sub-additive potential
![]() $\Phi =\{\phi _n\}_{n\ge 1}$
on X, put
$\Phi =\{\phi _n\}_{n\ge 1}$
on X, put
 $$ \begin{align*}P_n(f, \Phi, \epsilon)=\sup\bigg\{\sum_{x\in F}e^{\phi_n(x)}| F\ \mbox{is an}\ (n, \epsilon)\mbox{-separated subset of } X\bigg\}.\end{align*} $$
$$ \begin{align*}P_n(f, \Phi, \epsilon)=\sup\bigg\{\sum_{x\in F}e^{\phi_n(x)}| F\ \mbox{is an}\ (n, \epsilon)\mbox{-separated subset of } X\bigg\}.\end{align*} $$
Definition 2.1. We call the following quantity
the sub-additive topological pressure of
![]() $(f,\Phi )$
.
$(f,\Phi )$
.
Remark 2.1. If
![]() $\Phi =\{\phi _n\}_{n\geq 1}$
is additive in the sense that
$\Phi =\{\phi _n\}_{n\geq 1}$
is additive in the sense that
![]() $\phi _n(x)=\phi (x)+\phi (fx)+\cdots +\phi (f^{n-1}x)$
for some continuous function
$\phi _n(x)=\phi (x)+\phi (fx)+\cdots +\phi (f^{n-1}x)$
for some continuous function
![]() $\phi : X\to \mathbb {R}$
, we simply write
$\phi : X\to \mathbb {R}$
, we simply write
![]() $P(f, \Phi )$
as
$P(f, \Phi )$
as
![]() $P(f, \phi )$
. If it is clear from the context of the dynamics, we will simplify the topological pressure as
$P(f, \phi )$
. If it is clear from the context of the dynamics, we will simplify the topological pressure as
![]() $P(\phi )$
.
$P(\phi )$
.
Cao, Feng, and Huang [Reference Cao, Feng and Huang9] proved the following variational principle:
where
![]() $\mathcal {M}_f(X)$
denotes the space of all f-invariant measures on X,
$\mathcal {M}_f(X)$
denotes the space of all f-invariant measures on X,
![]() $h_\mu (f)$
denotes the metric entropy of f with respect to
$h_\mu (f)$
denotes the metric entropy of f with respect to
![]() $\mu $
(see [Reference Walters27] for details of metric entropy), and
$\mu $
(see [Reference Walters27] for details of metric entropy), and
for every
![]() $\mu \in \mathcal {M}_f(X)$
. The previous limit is well defined. A standard sub-additive argument yields the existence of this limit. A measure
$\mu \in \mathcal {M}_f(X)$
. The previous limit is well defined. A standard sub-additive argument yields the existence of this limit. A measure
![]() $\mu \in \mathcal {M}_f(X)$
that attains the supermum in equation (2.2) is called an equilibrium state of the topological pressure
$\mu \in \mathcal {M}_f(X)$
that attains the supermum in equation (2.2) is called an equilibrium state of the topological pressure
![]() $P(f,\Phi )$
.
$P(f,\Phi )$
.
2.2 Dimensions of sets and measures
Now we recall the definitions of Hausdorff and box dimensions of subsets and measures. Given a subset
![]() $Z\subset X$
, for any
$Z\subset X$
, for any
![]() $s\ge 0$
, let
$s\ge 0$
, let
 $$ \begin{align*} \mathcal{H}_{\delta}^{s}(Z)=\inf\bigg\{\sum\limits_{i=1}^{\infty}(\mbox{diam} U_{i})^{s}:\{U_{i}\}_{i\ge1}\ \mbox{is\ a cover\ of } Z \ \mbox{with } \mbox{diam}U_{i}\le \delta, \text{ for all } i\ge1 \bigg\} \end{align*} $$
$$ \begin{align*} \mathcal{H}_{\delta}^{s}(Z)=\inf\bigg\{\sum\limits_{i=1}^{\infty}(\mbox{diam} U_{i})^{s}:\{U_{i}\}_{i\ge1}\ \mbox{is\ a cover\ of } Z \ \mbox{with } \mbox{diam}U_{i}\le \delta, \text{ for all } i\ge1 \bigg\} \end{align*} $$
and
The above limit exists, though the limit may be infinity. We call
![]() $\mathcal {H}^{s}(Z)$
the s-Hausdorff measure of Z.
$\mathcal {H}^{s}(Z)$
the s-Hausdorff measure of Z.
Definition 2.2. The following jump-up value of
![]() $\mathcal {H}^{s}(Z)$
$\mathcal {H}^{s}(Z)$
is called the Hausdorff dimension of Z. The lower and upper box dimension of Z are defined respectively by
where
![]() $N(Z,\delta )$
denotes the least number of balls of radius
$N(Z,\delta )$
denotes the least number of balls of radius
![]() $\delta $
that are needed to cover the set Z. If
$\delta $
that are needed to cover the set Z. If
![]() $\underline {\dim }_BZ=\overline {\dim }_BZ$
, we will denote the common value by
$\underline {\dim }_BZ=\overline {\dim }_BZ$
, we will denote the common value by
![]() $\dim _BZ$
and call it the box dimension of Z.
$\dim _BZ$
and call it the box dimension of Z.
Given a Borel probability measure
![]() $\mu $
on X, the following quantity
$\mu $
on X, the following quantity
 $$ \begin{align*} \begin{aligned} \dim_H\mu &=\inf\{\dim_HZ: Z\subset X \text{ and } \mu(Z)=1\}\\ &=\lim_{\delta\to 0} \inf\{\dim_HZ: Z\subset X \text{ and } \mu(Z)\ge1-\delta\} \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \dim_H\mu &=\inf\{\dim_HZ: Z\subset X \text{ and } \mu(Z)=1\}\\ &=\lim_{\delta\to 0} \inf\{\dim_HZ: Z\subset X \text{ and } \mu(Z)\ge1-\delta\} \end{aligned} \end{align*} $$
is called the Hausdorff dimension of the measure
![]() $\mu $
. Similarly, we call the following two quantities
$\mu $
. Similarly, we call the following two quantities
and
the lower box dimension and upper box dimension of
![]() $\mu $
, respectively.
$\mu $
, respectively.
If
![]() $\mu $
is a finite measure on X, the following quantities
$\mu $
is a finite measure on X, the following quantities
are called lower and upper point-wise dimensions of
![]() $\mu $
at point x, respectively, where
$\mu $
at point x, respectively, where
![]() $B_{r}(x)=\{y\in X:d(x,y)< r\}$
. We recall two basic properties relating these quantities with the Hausdorff dimension of subsets and measures (see [Reference Pesin21] for details):
$B_{r}(x)=\{y\in X:d(x,y)< r\}$
. We recall two basic properties relating these quantities with the Hausdorff dimension of subsets and measures (see [Reference Pesin21] for details):
-
(1) if
 $\underline d_{\mu }(x) \geqslant a$
for
$\underline d_{\mu }(x) \geqslant a$
for
 $\mu $
almost every
$\mu $
almost every
 $x \in \Lambda $
, then
$x \in \Lambda $
, then
 $\operatorname {dim}_{H} \mu \geqslant a$
;
$\operatorname {dim}_{H} \mu \geqslant a$
; -
(2) if
 $\underline d_{\mu }(x)\leqslant a$
for every
$\underline d_{\mu }(x)\leqslant a$
for every
 $x \in Z \subset \Lambda $
, then
$x \in Z \subset \Lambda $
, then
 $\operatorname {dim}_{H} Z \leqslant a$
.
$\operatorname {dim}_{H} Z \leqslant a$
.
2.3 Measures of full Carathéodory singular dimension for repellers
In this section, we will recall the concept of Carathéodory singular dimension of subsets and invariant measures. For a non-conformal repeller of a
![]() $C^1$
map, we will show that there exists an ergodic measure of full Carathéodory singular dimension.
$C^1$
map, we will show that there exists an ergodic measure of full Carathéodory singular dimension.
2.3.1 Singular valued potentials
Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^1$
transformation of a
$C^1$
transformation of a
![]() $m_0$
-dimensional compact smooth Riemannian manifold M, and let
$m_0$
-dimensional compact smooth Riemannian manifold M, and let
![]() $\Lambda $
be a compact f-invariant subset of M. Denote by
$\Lambda $
be a compact f-invariant subset of M. Denote by
![]() $\mathcal {M}(f|_\Lambda )$
and
$\mathcal {M}(f|_\Lambda )$
and
![]() $\mathcal {E}(f|_\Lambda )$
the set of all f-invariant measures and ergodic measures on
$\mathcal {E}(f|_\Lambda )$
the set of all f-invariant measures and ergodic measures on
![]() $\Lambda $
, respectively.
$\Lambda $
, respectively.
If a compact f-invariant subset
![]() $\Lambda $
satisfies the following two properties:
$\Lambda $
satisfies the following two properties:
-
(1) there exists an open neighborhood U of
 $\Lambda $
such that
$\Lambda $
such that
 $\Lambda =\{x\in U: f^n(x)\in U \text { for all } n\ge 0\}$
;
$\Lambda =\{x\in U: f^n(x)\in U \text { for all } n\ge 0\}$
; -
(2) there is
 $\kappa> 1 $
such that where
$\kappa> 1 $
such that where $$ \begin{align*} \|D_xf v \| \ge \kappa \|v\| \quad \text{for all } x \in \Lambda, \quad\text{and}\ v \in T_xM, \end{align*} $$
$$ \begin{align*} \|D_xf v \| \ge \kappa \|v\| \quad \text{for all } x \in \Lambda, \quad\text{and}\ v \in T_xM, \end{align*} $$
 $\|\cdot \|$
is the norm induced by the Riemannian metric on M, and
$\|\cdot \|$
is the norm induced by the Riemannian metric on M, and
 $D_xf:T_xM\rightarrow T_{f(x)}M$
is the differential operator,
$D_xf:T_xM\rightarrow T_{f(x)}M$
is the differential operator,
then we call
![]() $\Lambda $
a repeller for f or f is expanding on
$\Lambda $
a repeller for f or f is expanding on
![]() $\Lambda $
.
$\Lambda $
.
Given
![]() $x\in \Lambda $
and
$x\in \Lambda $
and
![]() $n\ge 1$
, denote the singular values of
$n\ge 1$
, denote the singular values of
![]() $D_xf^n$
(square roots of the eigenvalues of
$D_xf^n$
(square roots of the eigenvalues of
![]() $(D_xf^n)^*D_xf^n$
) in the decreasing order by
$(D_xf^n)^*D_xf^n$
) in the decreasing order by
For
![]() $t\in [0,m_0]$
, set
$t\in [0,m_0]$
, set
 $$ \begin{align} \varphi^{t}(x,f^n): =\sum_{i=m_0-[t]+1}^{m_0}\log\alpha_i(x,f^n) +(t-[t])\log\alpha_{m_0-[t]}(x,f^n). \end{align} $$
$$ \begin{align} \varphi^{t}(x,f^n): =\sum_{i=m_0-[t]+1}^{m_0}\log\alpha_i(x,f^n) +(t-[t])\log\alpha_{m_0-[t]}(x,f^n). \end{align} $$
The functions
![]() $x\mapsto \alpha _i(x,f^n)$
,
$x\mapsto \alpha _i(x,f^n)$
,
![]() $x\mapsto \varphi ^t(x,f^n)$
are continuous for every
$x\mapsto \varphi ^t(x,f^n)$
are continuous for every
![]() $n\ge 1$
, since f is smooth. It is easy to see that for all
$n\ge 1$
, since f is smooth. It is easy to see that for all
![]() $n,\ell \in \mathbb {N}$
,
$n,\ell \in \mathbb {N}$
,
Hence, the sequence of functions
![]() $ \Phi _f(t):=\{-\varphi ^t(\cdot ,f^n)\}_{n\ge 1} $
is sub-additive, which is called the sub-additive singular valued potentials.
$ \Phi _f(t):=\{-\varphi ^t(\cdot ,f^n)\}_{n\ge 1} $
is sub-additive, which is called the sub-additive singular valued potentials.
2.3.2 Carathéodory singular dimension of sets and measures
The Carathéodory singular dimension of a repeller is introduced in [Reference Cao, Pesin and Zhao11]. Following the approach in [Reference Cao, Pesin and Zhao11], we will introduce the notions of Carathéodory singular dimension of subsets and measures.
Let
![]() $B_n(x,r):=\{x\in M: d_n(x,y)<r\}$
. Given a subset
$B_n(x,r):=\{x\in M: d_n(x,y)<r\}$
. Given a subset
![]() $Z\subseteq \Lambda $
, for each small number
$Z\subseteq \Lambda $
, for each small number
![]() $r>0$
, let
$r>0$
, let
 $$ \begin{align*} m(Z,t,r):=\lim_{N\to\infty}\inf\bigg\{\sum_i\exp\Big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^{t}(y,f^{n_i})\Big)\bigg\}, \end{align*} $$
$$ \begin{align*} m(Z,t,r):=\lim_{N\to\infty}\inf\bigg\{\sum_i\exp\Big(\sup_{y\in B_{n_i}(x_i,r)}-\varphi^{t}(y,f^{n_i})\Big)\bigg\}, \end{align*} $$
where the infimum is taken over all collections
![]() $\{B_{n_i}(x_i,r)\}$
of Bowen’s balls with
$\{B_{n_i}(x_i,r)\}$
of Bowen’s balls with
![]() $x_i\in \Lambda $
,
$x_i\in \Lambda $
,
![]() $n_i\ge N$
that cover Z. It is easy to see that there is a critical point
$n_i\ge N$
that cover Z. It is easy to see that there is a critical point
Consequently, we call the following quantity
the Carathéodory singular dimension of Z. In particular, the Carathéodory singular dimension of the repeller
![]() $\Lambda $
is independent of sufficiently small
$\Lambda $
is independent of sufficiently small
![]() $r>0$
(see [Reference Cao, Pesin and Zhao11, Theorem 4.1]).
$r>0$
(see [Reference Cao, Pesin and Zhao11, Theorem 4.1]).
For each f-invariant measure
![]() $\mu $
supported on
$\mu $
supported on
![]() $\Lambda $
, let
$\Lambda $
, let
and the following quantity
is called the Carathéodory singular dimension of the measure
![]() $\mu $
.
$\mu $
.
Theorem A. Let
![]() $f: M\to M$
be a
$f: M\to M$
be a
![]() $C^{1}$
transformation of an
$C^{1}$
transformation of an
![]() $m_0$
-dimensional compact smooth Riemannian manifold M, and
$m_0$
-dimensional compact smooth Riemannian manifold M, and
![]() $\Lambda $
a repeller of f. Then there exists an f-invariant ergodic measure
$\Lambda $
a repeller of f. Then there exists an f-invariant ergodic measure
![]() $\mu $
such that
$\mu $
such that
2.4 Measures of full and maximal dimension for ACH sets
In this section, we first recall the concept of an average conformal hyperbolic set which is introduced in [Reference Wang, Wang, Cao and Zhao29]. By modifying the methods in [Reference Chung13], we construct a Borel probability measure (not necessarily invariant) of full Hausdorff dimension for ACH sets of
![]() $C^1$
diffeomorphisms. Following Barreira and Wolf’s approach [Reference Barreira and Wolf5], we prove that there exists an ergodic measure of maximal Hausdorff dimension for ACH sets of
$C^1$
diffeomorphisms. Following Barreira and Wolf’s approach [Reference Barreira and Wolf5], we prove that there exists an ergodic measure of maximal Hausdorff dimension for ACH sets of
![]() $C^{1+\alpha }$
diffeomorphisms.
$C^{1+\alpha }$
diffeomorphisms.
2.4.1 Definition of ACH
Let
![]() $f{\kern-0.5pt}:{\kern-0.5pt}M{\kern-0.5pt}\rightarrow{\kern-0.5pt} M$
be a
$f{\kern-0.5pt}:{\kern-0.5pt}M{\kern-0.5pt}\rightarrow{\kern-0.5pt} M$
be a
![]() $C^1$
diffeomorphism on a
$C^1$
diffeomorphism on a
![]() $m_0$
-dimensional compact Riemannian manifold. For each
$m_0$
-dimensional compact Riemannian manifold. For each
![]() $x \in M$
, the following quantities
$x \in M$
, the following quantities
 $$ \begin{align*}\|D_x f\|=\sup_{0\neq v\in T_x M} \frac{\|D_x f(v)\|}{\|v\|},\quad m(D_x f)=\inf_{0\neq v\in T_x M} \frac{\|D_x f(v)\|}{\|v\|}\end{align*} $$
$$ \begin{align*}\|D_x f\|=\sup_{0\neq v\in T_x M} \frac{\|D_x f(v)\|}{\|v\|},\quad m(D_x f)=\inf_{0\neq v\in T_x M} \frac{\|D_x f(v)\|}{\|v\|}\end{align*} $$
are respectively called the maximal norm and minimum norm of the differentiable operator
![]() $D_{x}f:T_{x}M\rightarrow T_{f(x)}M$
, where
$D_{x}f:T_{x}M\rightarrow T_{f(x)}M$
, where
![]() $\|\cdot \|$
is the norm induced by the Riemannian metric on M. A compact f-invariant subset
$\|\cdot \|$
is the norm induced by the Riemannian metric on M. A compact f-invariant subset
![]() $\Lambda \subset M$
is called a locally maximal hyperbolic set if there exists an open neighborhood U such that
$\Lambda \subset M$
is called a locally maximal hyperbolic set if there exists an open neighborhood U such that
![]() $ \Lambda =\bigcap _{n \in \mathbb {Z}} f^{n} U$
, and a continuous splitting of the tangent bundle
$ \Lambda =\bigcap _{n \in \mathbb {Z}} f^{n} U$
, and a continuous splitting of the tangent bundle
![]() $T_{x} M=E_{x}^{s} \oplus E_{x}^{u}$
, and constants
$T_{x} M=E_{x}^{s} \oplus E_{x}^{u}$
, and constants
![]() $0<\unicode{x3bb} <1, C>0$
such that for every
$0<\unicode{x3bb} <1, C>0$
such that for every
![]() $x \in \Lambda $
:
$x \in \Lambda $
:
-
(1)
 $D_{x} f(E_{x}^{u})=E_{f(x)}^{u} , D_{x} f(E_{x}^{s})=E_{f(x)}^{s};$
$D_{x} f(E_{x}^{u})=E_{f(x)}^{u} , D_{x} f(E_{x}^{s})=E_{f(x)}^{s};$
-
(2) for every
 $n \in \mathbb {N}$
, one has
$n \in \mathbb {N}$
, one has
 $\|D_{x} f^{-n}(v)\| \leqslant C \unicode{x3bb} ^n\|v\| \text { for all } v \in E_{x}^{u}$
, and
$\|D_{x} f^{-n}(v)\| \leqslant C \unicode{x3bb} ^n\|v\| \text { for all } v \in E_{x}^{u}$
, and
 $\|D_{x} f^{n}(v)\| \leqslant C\unicode{x3bb} ^n\|v\| \text { for all } v \in E_{x}^{s}$
.
$\|D_{x} f^{n}(v)\| \leqslant C\unicode{x3bb} ^n\|v\| \text { for all } v \in E_{x}^{s}$
.
For
![]() $x \in M$
and
$x \in M$
and
![]() $v\in T_{x}M$
, the Lyapunov exponent of v at x is the limit
$v\in T_{x}M$
, the Lyapunov exponent of v at x is the limit
whenever the limit exists. Given an invariant measure
![]() $\mu \in \mathcal {M}(f|_\Lambda )$
, by the Oseledec multiplicative ergodic theorem [Reference Oseledec20], for
$\mu \in \mathcal {M}(f|_\Lambda )$
, by the Oseledec multiplicative ergodic theorem [Reference Oseledec20], for
![]() $\mu $
-almost every x, every vector
$\mu $
-almost every x, every vector
![]() $v\in T_xM$
has a Lyapunov exponent, and they can be denoted by
$v\in T_xM$
has a Lyapunov exponent, and they can be denoted by
![]() $\unicode{x3bb} _{1}(x)\geqslant \unicode{x3bb} _{2}(x)\geqslant \cdots \geqslant \unicode{x3bb} _{m_0}(x)$
. Furthermore, if
$\unicode{x3bb} _{1}(x)\geqslant \unicode{x3bb} _{2}(x)\geqslant \cdots \geqslant \unicode{x3bb} _{m_0}(x)$
. Furthermore, if
![]() $\mu $
is ergodic, since the Lyapunov exponents are f-invariant, we write the Lyapunov exponents as
$\mu $
is ergodic, since the Lyapunov exponents are f-invariant, we write the Lyapunov exponents as
![]() $\unicode{x3bb} _{1}(\mu )\geqslant \unicode{x3bb} _{2}(\mu )\geqslant \cdots \geqslant \unicode{x3bb} _{m_0}(\mu )$
. Notice that
$\unicode{x3bb} _{1}(\mu )\geqslant \unicode{x3bb} _{2}(\mu )\geqslant \cdots \geqslant \unicode{x3bb} _{m_0}(\mu )$
. Notice that
![]() $\|D_x f\|=\|D_x f|_{E_{x}^{u}}\|, ~\|D_x f^{-1}\|=\|D_x f^{-1}|_{E_{x}^{s}}\|$
in the hyperbolic setting.
$\|D_x f\|=\|D_x f|_{E_{x}^{u}}\|, ~\|D_x f^{-1}\|=\|D_x f^{-1}|_{E_{x}^{s}}\|$
in the hyperbolic setting.
A hyperbolic set
![]() $\Lambda \subset M$
is called an average conformal hyperbolic set if for each
$\Lambda \subset M$
is called an average conformal hyperbolic set if for each
![]() $\mu \in \mathcal {E}(f|_\Lambda )$
, one has
$\mu \in \mathcal {E}(f|_\Lambda )$
, one has
![]() $\unicode{x3bb} _{1}(\mu )=\unicode{x3bb} _{2}(\mu )=\cdots =\unicode{x3bb} _{d_u}(\mu )>0$
and
$\unicode{x3bb} _{1}(\mu )=\unicode{x3bb} _{2}(\mu )=\cdots =\unicode{x3bb} _{d_u}(\mu )>0$
and
![]() $\unicode{x3bb} _{d_u+1}(\mu )=\unicode{x3bb} _{d_u+2}(\mu )=\cdots =\unicode{x3bb} _{m_0}(\mu )<0$
, where
$\unicode{x3bb} _{d_u+1}(\mu )=\unicode{x3bb} _{d_u+2}(\mu )=\cdots =\unicode{x3bb} _{m_0}(\mu )<0$
, where
![]() $d_u=\operatorname {dim} E^u$
and
$d_u=\operatorname {dim} E^u$
and
![]() $d_s=\operatorname {dim} E^s=m_0-d_u$
. In other words, it has only two Lyapunov exponents
$d_s=\operatorname {dim} E^s=m_0-d_u$
. In other words, it has only two Lyapunov exponents
![]() $\unicode{x3bb} _u(\nu )>0$
and
$\unicode{x3bb} _u(\nu )>0$
and
![]() $\unicode{x3bb} _s(\nu )<0$
with respect to each
$\unicode{x3bb} _s(\nu )<0$
with respect to each
![]() $\nu \in \mathcal {E}(f|_\Lambda )$
.
$\nu \in \mathcal {E}(f|_\Lambda )$
.
2.4.2 Statements of main results
Although we cannot obtain an invariant measure of full dimension even in the case of conformal hyperbolic dynamical systems (see [Reference Barreira4, Ch. 5] for a detailed description), the following result shows that there exists a measure (not necessarily invariant) of full dimension for ACH sets of a
![]() $C^{1}$
diffeomorphism.
$C^{1}$
diffeomorphism.
Theorem B. Let
![]() $f:M\rightarrow M$
be a
$f:M\rightarrow M$
be a
![]() $C^{1}$
diffeomorphism on a
$C^{1}$
diffeomorphism on a
![]() $m_0$
-dimensional compact Riemannian manifold, and let
$m_0$
-dimensional compact Riemannian manifold, and let
![]() $\Lambda \subset M$
be a compact locally maximal hyperbolic set such that
$\Lambda \subset M$
be a compact locally maximal hyperbolic set such that
![]() $f|_{\Lambda }$
is topologically mixing and average conformal. Then there exists a Borel probability measure
$f|_{\Lambda }$
is topologically mixing and average conformal. Then there exists a Borel probability measure
![]() $\mu $
on
$\mu $
on
![]() $\Lambda $
with support strictly inside
$\Lambda $
with support strictly inside
![]() $\Lambda $
such that
$\Lambda $
such that
Under the setting of the above theorem, if f is of
![]() $C^{1+\alpha }$
smoothness, then there exists an f-invariant ergodic measure of maximal dimension.
$C^{1+\alpha }$
smoothness, then there exists an f-invariant ergodic measure of maximal dimension.
Theorem C. Let
![]() $f:M\rightarrow M$
be a
$f:M\rightarrow M$
be a
![]() $C^{1+\alpha }$
diffeomorphism on an
$C^{1+\alpha }$
diffeomorphism on an
![]() $m_0$
-dimensional compact Riemannian manifold, and let
$m_0$
-dimensional compact Riemannian manifold, and let
![]() $\Lambda \subset M$
be a compact locally maximal hyperbolic set such that
$\Lambda \subset M$
be a compact locally maximal hyperbolic set such that
![]() $f|_{\Lambda }$
is topologically mixing and average conformal. Then there exists an f-invariant ergodic probability measure
$f|_{\Lambda }$
is topologically mixing and average conformal. Then there exists an f-invariant ergodic probability measure
![]() $\mu $
on
$\mu $
on
![]() $\Lambda $
such that
$\Lambda $
such that
3 Proofs
In this section, we provide the detailed proof of the main results in this paper.
3.1 Proof of Theorem A
By the definition of Carathéodory singular dimension of subsets and measures, for every
![]() $\mu \in \mathcal {M}(f|_{\Lambda })$
, we have that
$\mu \in \mathcal {M}(f|_{\Lambda })$
, we have that
for all sufficiently small
![]() $r>0$
, see [Reference Cao, Pesin and Zhao11, Theorem 4.1] for the first equality. Letting
$r>0$
, see [Reference Cao, Pesin and Zhao11, Theorem 4.1] for the first equality. Letting
![]() $r\to 0$
, one has
$r\to 0$
, one has
![]() $\dim _C \Lambda \ge \dim _{C}\mu $
for every
$\dim _C \Lambda \ge \dim _{C}\mu $
for every
![]() $\mu \in \mathcal {M}(f|_{\Lambda })$
. Hence, we have that
$\mu \in \mathcal {M}(f|_{\Lambda })$
. Hence, we have that
However, for each f-invariant measure
![]() $\mu $
, let
$\mu $
, let
It is easy to see that
![]() $P_\mu (f|_\Lambda , \Phi _f(t))=0$
has a unique root, since
$P_\mu (f|_\Lambda , \Phi _f(t))=0$
has a unique root, since
![]() $P_\mu (f|_\Lambda , \Phi _f(t))$
is strictly decreasing and continuous with respect to t. If
$P_\mu (f|_\Lambda , \Phi _f(t))$
is strictly decreasing and continuous with respect to t. If
![]() $\mu \in \mathcal {E}(f|_{\Lambda })$
, it follows from [Reference Cao, Wang and Zhao12, Theorem A] that
$\mu \in \mathcal {E}(f|_{\Lambda })$
, it follows from [Reference Cao, Wang and Zhao12, Theorem A] that
where
![]() $t_\mu $
is the unique solution of the equation
$t_\mu $
is the unique solution of the equation
![]() $P_\mu (f|_\Lambda , \Phi _f(t))=0$
. Let
$P_\mu (f|_\Lambda , \Phi _f(t))=0$
. Let
![]() $t^*$
be the unique zero of Bowen’s equation
$t^*$
be the unique zero of Bowen’s equation
![]() $P(f|_\Lambda ,\Phi _f(t))=0$
. Then
$P(f|_\Lambda ,\Phi _f(t))=0$
. Then
![]() $\dim _C\Lambda =t^*$
(see [Reference Cao, Pesin and Zhao11, Theorem 4.1] for details).
$\dim _C\Lambda =t^*$
(see [Reference Cao, Pesin and Zhao11, Theorem 4.1] for details).
Since f is expanding on
![]() $\Lambda $
, the map
$\Lambda $
, the map
![]() $\mu \mapsto P_\mu (f|_\Lambda , \Phi _f(t^*))$
is upper semi-continuous on
$\mu \mapsto P_\mu (f|_\Lambda , \Phi _f(t^*))$
is upper semi-continuous on
![]() $\mathcal {M}(f|_{\Lambda })$
. It follows from the variational principle of sub-additive topological pressure that there exists an f-invariant ergodic measure
$\mathcal {M}(f|_{\Lambda })$
. It follows from the variational principle of sub-additive topological pressure that there exists an f-invariant ergodic measure
![]() $\widetilde {\mu }$
so that
$\widetilde {\mu }$
so that
Hence,
This completes the proof of the theorem.
![]() $\square $
$\square $
3.2 Proof of Theorem B
We first recall some facts of average conformal hyperbolic sets. For each
![]() $x \in \Lambda $
, denote
$x \in \Lambda $
, denote
where
![]() $d_u=\dim E^u_x$
,
$d_u=\dim E^u_x$
,
![]() $d^s=\dim E^s_x$
, and
$d^s=\dim E^s_x$
, and
![]() $d_u+d_s=m_0$
. It is clear that
$d_u+d_s=m_0$
. It is clear that
![]() $\phi _u$
and
$\phi _u$
and
![]() $\phi _s$
are continuous functions, since f is a
$\phi _s$
are continuous functions, since f is a
![]() $C^1$
diffeomorphism. Furthermore, the following properties hold:
$C^1$
diffeomorphism. Furthermore, the following properties hold:
-
(1) for any
 $n\in \mathbb {Z}$
, one has
$n\in \mathbb {Z}$
, one has
 $m(D_{x} f^{n}|_{E_{x}^{i}}) \leqslant |\!\operatorname {det} D_{x} f^n|_{E_{x}^{i}}|^{{1}/{d_i}} \leqslant \|D_{x} f^{n}|_{E_{x}^{i}}\|$
and (3.2)uniformly on
$m(D_{x} f^{n}|_{E_{x}^{i}}) \leqslant |\!\operatorname {det} D_{x} f^n|_{E_{x}^{i}}|^{{1}/{d_i}} \leqslant \|D_{x} f^{n}|_{E_{x}^{i}}\|$
and (3.2)uniformly on $$ \begin{align} \lim _{n \rightarrow \pm\infty} \frac{1}{|n|}(\log \|D_{x} f^{n}|_{E_{x}^{i}} \|-\log m(D_{x} f^{n}|_{E_{x}^{i}}))=0 \end{align} $$
$$ \begin{align} \lim _{n \rightarrow \pm\infty} \frac{1}{|n|}(\log \|D_{x} f^{n}|_{E_{x}^{i}} \|-\log m(D_{x} f^{n}|_{E_{x}^{i}}))=0 \end{align} $$
 $\Lambda $
, for
$\Lambda $
, for
 $i \in \{u, s\}$
. In fact, let
$i \in \{u, s\}$
. In fact, let
 $\psi _n(x) = \log \|D_{x} f^{n}|_{E_{x}^{u}} \|-\log m (D_{x} f^{n} |_{E_{x}^{u}})$
. Then the sequence of continuous functions
$\psi _n(x) = \log \|D_{x} f^{n}|_{E_{x}^{u}} \|-\log m (D_{x} f^{n} |_{E_{x}^{u}})$
. Then the sequence of continuous functions
 $\Psi :=\{\psi _n\}_{n\ge 1}$
is sub-additive. By [Reference Morris19, Theorem A.3], one has The case of
$\Psi :=\{\psi _n\}_{n\ge 1}$
is sub-additive. By [Reference Morris19, Theorem A.3], one has The case of $$ \begin{align*} \begin{aligned} \lim_{n\to\infty}\frac{1}{n}\max_{x\in\Lambda }\psi_n(x)&=\sup\{\mathcal{L}_*(\Psi,\mu):\mu\in \mathcal{E}(f|_\Lambda)\}\\ &=\sup\{\unicode{x3bb}_1(\mu)-\unicode{x3bb}_{d_u}(\mu):\mu\in \mathcal{E}(f|_\Lambda)\}\\ &=0. \end{aligned} \end{align*} $$
$$ \begin{align*} \begin{aligned} \lim_{n\to\infty}\frac{1}{n}\max_{x\in\Lambda }\psi_n(x)&=\sup\{\mathcal{L}_*(\Psi,\mu):\mu\in \mathcal{E}(f|_\Lambda)\}\\ &=\sup\{\unicode{x3bb}_1(\mu)-\unicode{x3bb}_{d_u}(\mu):\mu\in \mathcal{E}(f|_\Lambda)\}\\ &=0. \end{aligned} \end{align*} $$
 $i=s$
can be proven in a similar fashion. This yields the uniformly convergence in equation (3.2). See [Reference Ban, Cao and Hu2, Theorem 4.2] for the detailed proof of the case of average conformal repellers;
$i=s$
can be proven in a similar fashion. This yields the uniformly convergence in equation (3.2). See [Reference Ban, Cao and Hu2, Theorem 4.2] for the detailed proof of the case of average conformal repellers;
-
(2) let
 $t_{u}$
and
$t_{u}$
and
 $t_{s}$
denote the unique root of
$t_{s}$
denote the unique root of
 $P(f|_\Lambda , t \phi _{u})=0$
and
$P(f|_\Lambda , t \phi _{u})=0$
and
 $P(f|_\Lambda , t \phi _{s})=0$
, respectively. Then (3.3)see [Reference Wang, Wang, Cao and Zhao29, Theorem A and Remark 7] for a detailed description.
$P(f|_\Lambda , t \phi _{s})=0$
, respectively. Then (3.3)see [Reference Wang, Wang, Cao and Zhao29, Theorem A and Remark 7] for a detailed description. $$ \begin{align} \dim_H \Lambda=\dim_B \Lambda =t_{u}+t_{s}, \end{align} $$
$$ \begin{align} \dim_H \Lambda=\dim_B \Lambda =t_{u}+t_{s}, \end{align} $$
Since f is hyperbolic on
![]() $\Lambda $
, it is expansive, so we let
$\Lambda $
, it is expansive, so we let
![]() $0<c<1$
be an expansive constant of
$0<c<1$
be an expansive constant of
![]() $f|_{\Lambda }$
. In the rest of the proof of Theorem B, we fix a small number
$f|_{\Lambda }$
. In the rest of the proof of Theorem B, we fix a small number
![]() $\delta>0$
. According to equation (3.2), there exists
$\delta>0$
. According to equation (3.2), there exists
![]() $N(\delta )$
such that
$N(\delta )$
such that
 $$ \begin{align*} 1 \leqslant \frac{\|D_{x} f^{n}|_{E_{x}^{u}}\|}{\exp\{-\sum_{i=0}^{n-1} \phi_{u}(f^{i} x)\}} \leqslant e^{n \delta},\quad e^{-\ell \delta}\leqslant \frac{\|D_{x} f^{-\ell}|_{E_{x}^{s}}\|} {\exp\{-\sum_{i=0}^{\ell-1} \phi_{s}(f^{-i} x)\}} \leqslant 1 \end{align*} $$
$$ \begin{align*} 1 \leqslant \frac{\|D_{x} f^{n}|_{E_{x}^{u}}\|}{\exp\{-\sum_{i=0}^{n-1} \phi_{u}(f^{i} x)\}} \leqslant e^{n \delta},\quad e^{-\ell \delta}\leqslant \frac{\|D_{x} f^{-\ell}|_{E_{x}^{s}}\|} {\exp\{-\sum_{i=0}^{\ell-1} \phi_{s}(f^{-i} x)\}} \leqslant 1 \end{align*} $$
for any
![]() $n,\ell \geqslant N(\delta )$
and any
$n,\ell \geqslant N(\delta )$
and any
![]() $x\in \Lambda $
. Fix a positive integer
$x\in \Lambda $
. Fix a positive integer
![]() $L\geqslant N(\delta )$
. It follows from the uniform continuity of the map
$L\geqslant N(\delta )$
. It follows from the uniform continuity of the map
![]() $x \mapsto \|D_{x} f^{L}\|$
that there exists
$x \mapsto \|D_{x} f^{L}\|$
that there exists
![]() $~0<\varepsilon _{0}<{c}/{4}~$
such that
$~0<\varepsilon _{0}<{c}/{4}~$
such that
 $$ \begin{align*} e^{-\delta} \leqslant \frac{\|D_{z} f^{L}\|}{\|D_{y} f^{L}\|} \leqslant e^{\delta} \quad\text{and}\quad e^{-\delta} \leqslant \frac{\|D_{z} f^{-L}\|}{\|D_{y} f^{-L}\|} \leqslant e^{\delta} \end{align*} $$
$$ \begin{align*} e^{-\delta} \leqslant \frac{\|D_{z} f^{L}\|}{\|D_{y} f^{L}\|} \leqslant e^{\delta} \quad\text{and}\quad e^{-\delta} \leqslant \frac{\|D_{z} f^{-L}\|}{\|D_{y} f^{-L}\|} \leqslant e^{\delta} \end{align*} $$
for any
![]() $y,z\in \Lambda $
with
$y,z\in \Lambda $
with
![]() $d(y,z)<\varepsilon _{0}$
.
$d(y,z)<\varepsilon _{0}$
.
Choose a Markov partition
![]() $\mathcal {R}=\{R_{1}, \ldots , R_{s}\}$
of
$\mathcal {R}=\{R_{1}, \ldots , R_{s}\}$
of
![]() $\Lambda $
such that
$\Lambda $
such that
and
![]() $\#\{1 \leqslant q \leqslant s: R_{p} \cap R_{q}=\varnothing \}>0$
for every
$\#\{1 \leqslant q \leqslant s: R_{p} \cap R_{q}=\varnothing \}>0$
for every
![]() $p\in \{1,\ldots ,s\}$
(see [Reference Bowen7]). Let
$p\in \{1,\ldots ,s\}$
(see [Reference Bowen7]). Let
![]() $A=(a_{i j})_{1\leqslant i,j\leqslant s}$
be the structure matrix of
$A=(a_{i j})_{1\leqslant i,j\leqslant s}$
be the structure matrix of
![]() $\mathcal {R}$
and
$\mathcal {R}$
and
![]() $(\Sigma _{A}, \sigma )$
be the corresponding Markov subshift. We denote the set of all words of length n of
$(\Sigma _{A}, \sigma )$
be the corresponding Markov subshift. We denote the set of all words of length n of
![]() $\Sigma _{A}$
by
$\Sigma _{A}$
by
![]() $\Sigma {(n)}$
and let
$\Sigma {(n)}$
and let
for each
![]() $\mathbf {a}=(a_{i}) \in \Sigma _{A}$
and
$\mathbf {a}=(a_{i}) \in \Sigma _{A}$
and
![]() $k, \ell \in \mathbb {N}$
. Define a coding map
$k, \ell \in \mathbb {N}$
. Define a coding map
![]() $h:\Sigma _{A}\rightarrow \Lambda $
by
$h:\Sigma _{A}\rightarrow \Lambda $
by
 $$ \begin{align*}h({}_{-k}[a_{-k} \ldots a_{0} \ldots a_{\ell}] _{\ell})=\bigcap_{j=-k}^{\ell} f^{-j} R_{a_{j}}\quad\text{for all }(a_{-k}\ldots a_{\ell}) \in \Sigma(k+\ell+1),\end{align*} $$
$$ \begin{align*}h({}_{-k}[a_{-k} \ldots a_{0} \ldots a_{\ell}] _{\ell})=\bigcap_{j=-k}^{\ell} f^{-j} R_{a_{j}}\quad\text{for all }(a_{-k}\ldots a_{\ell}) \in \Sigma(k+\ell+1),\end{align*} $$
then the map h is a continuous surjection which satisfies
![]() $h \circ \sigma =f \circ h$
. Let
$h \circ \sigma =f \circ h$
. Let
 $$ \begin{align*}\mathcal{R}(-k, \ell)=\bigg\{\bigcap_{j=-k}^{\ell} f^{-j} R_{a_{j}}:(a_{-k} \ldots a_{\ell}) \in \Sigma(k+\ell+1)\bigg\}.\end{align*} $$
$$ \begin{align*}\mathcal{R}(-k, \ell)=\bigg\{\bigcap_{j=-k}^{\ell} f^{-j} R_{a_{j}}:(a_{-k} \ldots a_{\ell}) \in \Sigma(k+\ell+1)\bigg\}.\end{align*} $$
Since h is bounded finite to one (see [Reference Aoki1]), there is an integer
![]() $e_{0}>0$
such that
$e_{0}>0$
such that
for every
![]() $x \in \Lambda $
and
$x \in \Lambda $
and
![]() $k, \ell \in \mathbb {N}$
.
$k, \ell \in \mathbb {N}$
.
We construct the desired Borel probability measure as follows. Since
![]() $t_u \phi _{u} \circ h$
and
$t_u \phi _{u} \circ h$
and
![]() $t_s \phi _{s} \circ h$
are continuous functions and
$t_s \phi _{s} \circ h$
are continuous functions and
there exist two weak Gibbs measures
![]() $m_+, m_-$
on
$m_+, m_-$
on
![]() $\Sigma _{A}$
in the sense that there exist two sequences of positive constants
$\Sigma _{A}$
in the sense that there exist two sequences of positive constants
![]() $\{A_\ell \}_{\ell \in \mathbb {N}}$
and
$\{A_\ell \}_{\ell \in \mathbb {N}}$
and
![]() $\{B_k\}_{k\in \mathbb {N}}$
satisfying
$\{B_k\}_{k\in \mathbb {N}}$
satisfying
![]() $\lim _{\ell \rightarrow \infty } ({1}/{\ell }) \log A_{\ell }=0$
and
$\lim _{\ell \rightarrow \infty } ({1}/{\ell }) \log A_{\ell }=0$
and
![]() $\lim _{k \rightarrow \infty } ({1}/{k}) \log B_{k}=0$
such that
$\lim _{k \rightarrow \infty } ({1}/{k}) \log B_{k}=0$
such that
 $$ \begin{align*} \frac{1}{A_{l+1}} \leqslant \frac{m_{+}({}_{0}[a_{0} \ldots a_{l}]_{l})}{\exp \bigg\{\sum_{j=0}^{l} t_{u} \phi_{u}\circ h(\sigma^{j} \mathbf{a})\bigg\}} \leqslant A_{l+1} \end{align*} $$
$$ \begin{align*} \frac{1}{A_{l+1}} \leqslant \frac{m_{+}({}_{0}[a_{0} \ldots a_{l}]_{l})}{\exp \bigg\{\sum_{j=0}^{l} t_{u} \phi_{u}\circ h(\sigma^{j} \mathbf{a})\bigg\}} \leqslant A_{l+1} \end{align*} $$
and
 $$ \begin{align*} \frac{1}{B_{k+1}} \leqslant \frac{m_{-}({}_{-k}[a_{-k} \ldots a_{0}]_{0})}{\exp \bigg\{\sum_{j=0}^{k} t_{s} \phi_{s}\circ h(\sigma^{-j} \mathbf{a})\bigg\}} \leqslant B_{k+1} \end{align*} $$
$$ \begin{align*} \frac{1}{B_{k+1}} \leqslant \frac{m_{-}({}_{-k}[a_{-k} \ldots a_{0}]_{0})}{\exp \bigg\{\sum_{j=0}^{k} t_{s} \phi_{s}\circ h(\sigma^{-j} \mathbf{a})\bigg\}} \leqslant B_{k+1} \end{align*} $$
for every
![]() $\mathbf {a}=(a_i)\in \Sigma _{A}$
and
$\mathbf {a}=(a_i)\in \Sigma _{A}$
and
![]() $k,\ell \in \mathbb {N}$
(see [Reference Barreira3, pp. 289]).
$k,\ell \in \mathbb {N}$
(see [Reference Barreira3, pp. 289]).
Let m be a Borel probability measure on
![]() $\Sigma _{A}$
such that
$\Sigma _{A}$
such that
 $$ \begin{align*}m({}_{-k}[a_{-k} \ldots a_{0} \ldots a_{\ell}]_{\ell})=\begin{cases} C_{1}m_{+}({}_{0}[a_{0} \ldots a_{\ell}]_{\ell}) m_{-}({}_{-k}[a_{-k} \ldots a_{0}]_{0}), & a_0=1,\\ 0, &a_0 \neq 1, \end{cases}\end{align*} $$
$$ \begin{align*}m({}_{-k}[a_{-k} \ldots a_{0} \ldots a_{\ell}]_{\ell})=\begin{cases} C_{1}m_{+}({}_{0}[a_{0} \ldots a_{\ell}]_{\ell}) m_{-}({}_{-k}[a_{-k} \ldots a_{0}]_{0}), & a_0=1,\\ 0, &a_0 \neq 1, \end{cases}\end{align*} $$
for every
![]() $\mathbf {a}=(a_i)\in \Sigma _{A}$
,
$\mathbf {a}=(a_i)\in \Sigma _{A}$
,
![]() $k,\ell \in \mathbb {N}$
, and
$k,\ell \in \mathbb {N}$
, and
![]() $C_{1}=m_{+}({}_{0}[1]_{0})^{-1} m_{-}({}_{0}[1]_{0})^{-1}.$
$C_{1}=m_{+}({}_{0}[1]_{0})^{-1} m_{-}({}_{0}[1]_{0})^{-1}.$
Define a Borel probability measure
![]() $\mu $
on
$\mu $
on
![]() $\Lambda $
by
$\Lambda $
by
for each Borel subset
![]() $A\subset \Lambda $
. It is clear from the definition that the support of
$A\subset \Lambda $
. It is clear from the definition that the support of
![]() $\mu $
is
$\mu $
is
![]() $R_{1}$
. Furthermore, if
$R_{1}$
. Furthermore, if
![]() $a_{0}=1\text { and }(a_{-k} \ldots a_{0} \ldots a_{\ell }) \in \Sigma (k+\ell +1),~k,\ell \in \mathbb {N}$
, then we have that for
$a_{0}=1\text { and }(a_{-k} \ldots a_{0} \ldots a_{\ell }) \in \Sigma (k+\ell +1),~k,\ell \in \mathbb {N}$
, then we have that for
![]() $ x \in \bigcap _{j=-k}^{\ell } f^{-j} R_{a_{j}}$
,
$ x \in \bigcap _{j=-k}^{\ell } f^{-j} R_{a_{j}}$
,
 $$ \begin{align} \frac{C_{1}}{A_{\ell+1}B_{k+1}} \leqslant \frac{\mu(\bigcap_{j=-k}^{\ell} f^{-j} R_{a_{j}})}{\exp \{\sum_{i=0}^{\ell} t_{u} \phi_{u} (f^{i} x)+\sum_{j=0}^{k} t_{s} \phi_{s} (f^{-j} x)\}} \leqslant C_{1}A_{\ell+1}B_{k+1}. \end{align} $$
$$ \begin{align} \frac{C_{1}}{A_{\ell+1}B_{k+1}} \leqslant \frac{\mu(\bigcap_{j=-k}^{\ell} f^{-j} R_{a_{j}})}{\exp \{\sum_{i=0}^{\ell} t_{u} \phi_{u} (f^{i} x)+\sum_{j=0}^{k} t_{s} \phi_{s} (f^{-j} x)\}} \leqslant C_{1}A_{\ell+1}B_{k+1}. \end{align} $$
To prove Theorem B, we first prove some auxiliary results.
Lemma 3.1. Let
![]() $f:M\rightarrow M$
be a
$f:M\rightarrow M$
be a
![]() $C^{1}$
diffeomorphism on an
$C^{1}$
diffeomorphism on an
![]() $m_0$
-dimensional compact Riemannian manifold, and let
$m_0$
-dimensional compact Riemannian manifold, and let
![]() $\Lambda \subset M$
be a compact locally maximal hyperbolic set such that
$\Lambda \subset M$
be a compact locally maximal hyperbolic set such that
![]() $f|_{\Lambda }$
is topologically mixing and average conformal. There exists
$f|_{\Lambda }$
is topologically mixing and average conformal. There exists
![]() $\varepsilon _0>0$
(make
$\varepsilon _0>0$
(make
![]() $\varepsilon _0$
small if necessarily) such that for any
$\varepsilon _0$
small if necessarily) such that for any
![]() $n,m\in \mathbb {N}$
, if
$n,m\in \mathbb {N}$
, if
![]() $ x,z\in \Lambda $
satisfy
$ x,z\in \Lambda $
satisfy
![]() $\max _{0 \leqslant j \leqslant n-1} d(f^{j} x, f^{j} z) <\varepsilon _0$
and
$\max _{0 \leqslant j \leqslant n-1} d(f^{j} x, f^{j} z) <\varepsilon _0$
and
![]() $ y,w\in \Lambda $
satisfy
$ y,w\in \Lambda $
satisfy
![]() $\max _{0 \leqslant j \leqslant m-1} d(f^{-j} y, f^{-j} w) <\varepsilon _0$
, then
$\max _{0 \leqslant j \leqslant m-1} d(f^{-j} y, f^{-j} w) <\varepsilon _0$
, then
 $$ \begin{align*} e^{-n\delta} < \frac{|\!\det D_{z} f^{n}|_{E^u_{z}}|^{{1}/{d_{u}}}}{|\!\det D_{x} f^{n}|_{E^u_{x}}|^{{1}/{d_{u}}}} < e^{n\delta} \end{align*} $$
$$ \begin{align*} e^{-n\delta} < \frac{|\!\det D_{z} f^{n}|_{E^u_{z}}|^{{1}/{d_{u}}}}{|\!\det D_{x} f^{n}|_{E^u_{x}}|^{{1}/{d_{u}}}} < e^{n\delta} \end{align*} $$
and
 $$ \begin{align*} e^{-m\delta} < \frac{|\!\det D_{w} f^{-m}|_{E^s_{w}}|^{{1}/{d_{s}}}}{|\!\det D_{y} f^{-m}|_{E^s_{y}}|^{{1}/{d_{s}}}} < e^{m\delta}. \end{align*} $$
$$ \begin{align*} e^{-m\delta} < \frac{|\!\det D_{w} f^{-m}|_{E^s_{w}}|^{{1}/{d_{s}}}}{|\!\det D_{y} f^{-m}|_{E^s_{y}}|^{{1}/{d_{s}}}} < e^{m\delta}. \end{align*} $$
Proof. Since
![]() $\log |\!\operatorname {det} D_xf|$
is uniformly continuous on
$\log |\!\operatorname {det} D_xf|$
is uniformly continuous on
![]() $\Lambda $
, there exists
$\Lambda $
, there exists
![]() $\varepsilon _0>0$
such that if
$\varepsilon _0>0$
such that if
![]() $d(x,z)<\varepsilon _0$
, then
$d(x,z)<\varepsilon _0$
, then
Hence, if
![]() $ x,z\in \Lambda $
satisfy
$ x,z\in \Lambda $
satisfy
![]() $\max _{0 \leqslant j \leqslant n-1} d(f^{j} x, f^{j} z) <\varepsilon _0$
, then
$\max _{0 \leqslant j \leqslant n-1} d(f^{j} x, f^{j} z) <\varepsilon _0$
, then
 $$ \begin{align*} \bigg|\log \frac{|\det D_{z} f^{n}|_{E^u_{z}}|^{{1}/{d_u}}}{|\det D_{x} f^{n}|_{E^u_{x}}|^{{1}/{d_u}}}\bigg| &\le \sum_{j=0}^{n-1}\bigg|\log \frac{|\operatorname {det} D_{f^{j} z} f|_{E^u_{f^{j} z}}|^{{1}/{d_u}}}{|\det D_{f^{j} x} f|_{E^u_{f^{j} x}}|^{{1}/{d_{u}}}}\bigg|\\ &< n\delta. \end{align*} $$
$$ \begin{align*} \bigg|\log \frac{|\det D_{z} f^{n}|_{E^u_{z}}|^{{1}/{d_u}}}{|\det D_{x} f^{n}|_{E^u_{x}}|^{{1}/{d_u}}}\bigg| &\le \sum_{j=0}^{n-1}\bigg|\log \frac{|\operatorname {det} D_{f^{j} z} f|_{E^u_{f^{j} z}}|^{{1}/{d_u}}}{|\det D_{f^{j} x} f|_{E^u_{f^{j} x}}|^{{1}/{d_{u}}}}\bigg|\\ &< n\delta. \end{align*} $$
The other one can be proven in a similar fashion. This completes the proof of the lemma.
Set
![]() $\delta _{0}=\inf \{ d(x, y):\ x \in R_{p},\ y \in R_{q},\ R_{p} \cap R_{q}=\emptyset ,\ 1 \leqslant p<q \leqslant s \}>0$
,
$\delta _{0}=\inf \{ d(x, y):\ x \in R_{p},\ y \in R_{q},\ R_{p} \cap R_{q}=\emptyset ,\ 1 \leqslant p<q \leqslant s \}>0$
,
![]() $ r_{0}=\min \{{\delta _{0}}/{2}, {\varepsilon _{0}}/{2}\}>0$
, and
$ r_{0}=\min \{{\delta _{0}}/{2}, {\varepsilon _{0}}/{2}\}>0$
, and
![]() $ C_2=\max _{1 \leqslant i \leqslant {L-1}} \max _{x\in M}\{\|D_{x} f^{i}\|\}$
.
$ C_2=\max _{1 \leqslant i \leqslant {L-1}} \max _{x\in M}\{\|D_{x} f^{i}\|\}$
.
Lemma 3.2. For
![]() $n, \ell> L\geqslant N(\delta )$
, if
$n, \ell> L\geqslant N(\delta )$
, if
![]() $x\in \Lambda $
and
$x\in \Lambda $
and
![]() $0<r<r_0$
satisfy that
$0<r<r_0$
satisfy that
![]() $ C_{2} r \exp \{2n \delta -\sum _{i=0}^{n-1} \phi _{u}(f^{i} x)\}<r_0$
and
$ C_{2} r \exp \{2n \delta -\sum _{i=0}^{n-1} \phi _{u}(f^{i} x)\}<r_0$
and
![]() $C_{2} r \exp \{2\ell \delta -\sum _{i=0}^{\ell -1} \phi _{s}(f^{-i} x)\}<r_{0}$
, then
$C_{2} r \exp \{2\ell \delta -\sum _{i=0}^{\ell -1} \phi _{s}(f^{-i} x)\}<r_{0}$
, then
where
![]() $B_{r_{0}}^{f}(x,-\ell , n)=\{z \in M: d(f^{j} x, f^{j} z) < r_{0}, \text { for all } j=-\ell , \ldots , n\}.$
$B_{r_{0}}^{f}(x,-\ell , n)=\{z \in M: d(f^{j} x, f^{j} z) < r_{0}, \text { for all } j=-\ell , \ldots , n\}.$
Proof. Take
![]() $y\in B_{r}(x)$
, we first show that
$y\in B_{r}(x)$
, we first show that
![]() $ d(f^{j} x, f^{j} y) < r_{0}$
for every
$ d(f^{j} x, f^{j} y) < r_{0}$
for every
![]() $j=1, \ldots , n$
if
$j=1, \ldots , n$
if
![]() $ C_{2} r \exp \{2n \delta -\sum _{i=0}^{n-1} \phi _{u}(f^{i} x)\}<r_0.$
$ C_{2} r \exp \{2n \delta -\sum _{i=0}^{n-1} \phi _{u}(f^{i} x)\}<r_0.$
Choose
![]() $0<\varepsilon _{1}<{\varepsilon _{0}}/{2}$
so small that
$0<\varepsilon _{1}<{\varepsilon _{0}}/{2}$
so small that
![]() $ C_{2}(r+\varepsilon _{1}) \exp \{2n \delta -\sum _{i=0}^{n-1} \phi _{u}(f^{i} x)\}<r_{0}$
. According to the definition of the Riemannian metric, there exists a smooth curve
$ C_{2}(r+\varepsilon _{1}) \exp \{2n \delta -\sum _{i=0}^{n-1} \phi _{u}(f^{i} x)\}<r_{0}$
. According to the definition of the Riemannian metric, there exists a smooth curve
![]() $\xi :[0,1]\rightarrow M$
such that
$\xi :[0,1]\rightarrow M$
such that
 $$ \begin{align*}\xi(0)=x,~\xi(1)=y\quad\text{and}\quad\int_{0}^{1}\|\dot{\xi} (s)\| \,d s \le r+\varepsilon_{1}.\end{align*} $$
$$ \begin{align*}\xi(0)=x,~\xi(1)=y\quad\text{and}\quad\int_{0}^{1}\|\dot{\xi} (s)\| \,d s \le r+\varepsilon_{1}.\end{align*} $$
Since
 $$ \begin{align*}d(x, \xi(t)) \leqslant \int_{0}^{t}\|\dot{\xi}(s)\|\, d s\leqslant r+\varepsilon_{1}<\varepsilon_{0}~(0\leqslant t \leqslant 1),\end{align*} $$
$$ \begin{align*}d(x, \xi(t)) \leqslant \int_{0}^{t}\|\dot{\xi}(s)\|\, d s\leqslant r+\varepsilon_{1}<\varepsilon_{0}~(0\leqslant t \leqslant 1),\end{align*} $$
we have
 $$ \begin{align*} d(f^{L}x, f^{L}\xi(t)) &\le \int_{0}^{t}\|D_{\xi(s)} f^L\| \cdot\|\dot{\xi}(s)\|\, d s\\[-2pt]&\leqslant e^\delta\|D_{x} f^L\|\int_{0}^{t}\|\dot{\xi}(s)\|\, d s\\[-2pt]&= e^\delta\|D_{x} f^L|_{E^u_{x}}\|\int_{0}^{t}\|\dot{\xi}(s)\|\, d s\\[-2pt]&\leqslant (r+\varepsilon_{1}) e^{(L+1) \delta}\cdot \prod_{i=0}^{L-1}\|\!\det D_{f^{i} x} f|_{E_{f^{i} x}^{u}}\|^{{1}/{d_u}}\\[-2pt]&= (r+\varepsilon_{1}) \exp \bigg\{(L+1) \delta-\sum_{i=0}^{L-1} \phi_{u}(f^{i} x)\bigg\}\\[-2pt]&<r_{0}(<\varepsilon_{0}). \end{align*} $$
$$ \begin{align*} d(f^{L}x, f^{L}\xi(t)) &\le \int_{0}^{t}\|D_{\xi(s)} f^L\| \cdot\|\dot{\xi}(s)\|\, d s\\[-2pt]&\leqslant e^\delta\|D_{x} f^L\|\int_{0}^{t}\|\dot{\xi}(s)\|\, d s\\[-2pt]&= e^\delta\|D_{x} f^L|_{E^u_{x}}\|\int_{0}^{t}\|\dot{\xi}(s)\|\, d s\\[-2pt]&\leqslant (r+\varepsilon_{1}) e^{(L+1) \delta}\cdot \prod_{i=0}^{L-1}\|\!\det D_{f^{i} x} f|_{E_{f^{i} x}^{u}}\|^{{1}/{d_u}}\\[-2pt]&= (r+\varepsilon_{1}) \exp \bigg\{(L+1) \delta-\sum_{i=0}^{L-1} \phi_{u}(f^{i} x)\bigg\}\\[-2pt]&<r_{0}(<\varepsilon_{0}). \end{align*} $$
Furthermore, we have that
 $$ \begin{align*} d(f^{2L}x, f^{2L}\xi(t)) &\leqslant \int_{0}^{t}\|D_{\xi(s)} f^L\|\cdot\|D_{f^{L}\xi(s)} f^L\| \cdot\|\dot{\xi}(s)\| \,d s\\ &\leqslant e^{2\delta}\|D_{x} f^L\|\cdot\|D_{f^{L}x} f^L\|\int_{0}^{t}\|\dot{\xi}(s)\| \,d s\\ &= e^{2\delta}\|D_{x} f^L|_{E^u_{x}}\|\cdot\|D_{f^{L}x} f^L|_{E^u_{f^L x}}\|\int_{0}^{t}\|\dot{\xi}(s)\| \,d s\\ &\leqslant (r+\varepsilon_{1}) e^{2(L+1) \delta}\cdot\prod_{i=0}^{2L-1} \|\!\operatorname {det} D_{f^{i} x} f|_{E_{f^{i} x}^{u}}\|^{{1}/{d_u}}\\ &= (r+\varepsilon_{1}) \exp \bigg\{2(L+1) \delta-\sum_{i=0}^{2L-1} \phi_{u}(f^{i} x)\bigg\}. \end{align*} $$
$$ \begin{align*} d(f^{2L}x, f^{2L}\xi(t)) &\leqslant \int_{0}^{t}\|D_{\xi(s)} f^L\|\cdot\|D_{f^{L}\xi(s)} f^L\| \cdot\|\dot{\xi}(s)\| \,d s\\ &\leqslant e^{2\delta}\|D_{x} f^L\|\cdot\|D_{f^{L}x} f^L\|\int_{0}^{t}\|\dot{\xi}(s)\| \,d s\\ &= e^{2\delta}\|D_{x} f^L|_{E^u_{x}}\|\cdot\|D_{f^{L}x} f^L|_{E^u_{f^L x}}\|\int_{0}^{t}\|\dot{\xi}(s)\| \,d s\\ &\leqslant (r+\varepsilon_{1}) e^{2(L+1) \delta}\cdot\prod_{i=0}^{2L-1} \|\!\operatorname {det} D_{f^{i} x} f|_{E_{f^{i} x}^{u}}\|^{{1}/{d_u}}\\ &= (r+\varepsilon_{1}) \exp \bigg\{2(L+1) \delta-\sum_{i=0}^{2L-1} \phi_{u}(f^{i} x)\bigg\}. \end{align*} $$
Therefore, for every
![]() $j=1, \ldots , n $
, write
$j=1, \ldots , n $
, write
![]() $j=g_{j}L+t_{j}$
, where
$j=g_{j}L+t_{j}$
, where
![]() $g_{j}\in \mathbb {N}$
and
$g_{j}\in \mathbb {N}$
and
![]() $0\leqslant t_{j}< L$
, we have
$0\leqslant t_{j}< L$
, we have
 $$ \begin{align*} d(f^{j}x, f^{j}\xi(t)) &\leqslant \int_{0}^{t}\prod_{i=0}^{g_{j}-1}\|D_{f^{iL}\xi(s)} f^L\|\cdot\|D_{f^{g_{j}L}\xi(s)} f^{t_j}\| \cdot\|\dot{\xi}(s)\| \,d s\\[-2pt]&\leqslant C_{2}e^{g_{j}\delta}\cdot\prod_{i=0}^{g_{j}-1}\|D_{f^{iL}x}f^L\|\cdot\int_{0}^{t}\|\dot{\xi}(s)\| \,d s\\[-2pt]&\leqslant C_{2}(r+\varepsilon_{1}) \exp \bigg\{g_{j}(L+1) \delta-\sum_{i=0}^{g_{j}L-1} \phi_{u}(f^{i} x)\bigg\}\\[-2pt]&\leqslant C_{2}(r+\varepsilon_{1}) \exp \bigg\{2j\delta-\sum_{i=0}^{j-1} \phi_{u}(f^{i} x)\bigg\}\\[-2pt]&\leqslant C_{2}(r+\varepsilon_{1}) \exp \bigg\{2n\delta-\sum_{i=0}^{n-1} \phi_{u}(f^{i} x)\bigg\}\\[-2pt]&<r_0~(0\leqslant t \leqslant 1). \end{align*} $$
$$ \begin{align*} d(f^{j}x, f^{j}\xi(t)) &\leqslant \int_{0}^{t}\prod_{i=0}^{g_{j}-1}\|D_{f^{iL}\xi(s)} f^L\|\cdot\|D_{f^{g_{j}L}\xi(s)} f^{t_j}\| \cdot\|\dot{\xi}(s)\| \,d s\\[-2pt]&\leqslant C_{2}e^{g_{j}\delta}\cdot\prod_{i=0}^{g_{j}-1}\|D_{f^{iL}x}f^L\|\cdot\int_{0}^{t}\|\dot{\xi}(s)\| \,d s\\[-2pt]&\leqslant C_{2}(r+\varepsilon_{1}) \exp \bigg\{g_{j}(L+1) \delta-\sum_{i=0}^{g_{j}L-1} \phi_{u}(f^{i} x)\bigg\}\\[-2pt]&\leqslant C_{2}(r+\varepsilon_{1}) \exp \bigg\{2j\delta-\sum_{i=0}^{j-1} \phi_{u}(f^{i} x)\bigg\}\\[-2pt]&\leqslant C_{2}(r+\varepsilon_{1}) \exp \bigg\{2n\delta-\sum_{i=0}^{n-1} \phi_{u}(f^{i} x)\bigg\}\\[-2pt]&<r_0~(0\leqslant t \leqslant 1). \end{align*} $$
Setting
![]() $t=1$
, we obtain
$t=1$
, we obtain
![]() $d(f^{j} x, f^{j} y) \leqslant r_{0}$
for every
$d(f^{j} x, f^{j} y) \leqslant r_{0}$
for every
![]() $1\leqslant j\leqslant n$
. Analogously, one can show that
$1\leqslant j\leqslant n$
. Analogously, one can show that
![]() $d(f^{-j}x, f^{-j}y){\kern-1pt}<{\kern-1pt}r_0$
for
$d(f^{-j}x, f^{-j}y){\kern-1pt}<{\kern-1pt}r_0$
for
![]() $j{\kern-1pt}={\kern-1pt}1, \ldots , \ell $
if
$j{\kern-1pt}={\kern-1pt}1, \ldots , \ell $
if
![]() $ C_{2} r \exp \{2\ell \delta {\kern-1pt}-{\kern-1pt}\sum _{i=0}^{\ell -1} \phi _{s}(f^{-i} x)\}{\kern-1pt}<{\kern-1pt}r_{0}$
. This completes the proof of the lemma.
$ C_{2} r \exp \{2\ell \delta {\kern-1pt}-{\kern-1pt}\sum _{i=0}^{\ell -1} \phi _{s}(f^{-i} x)\}{\kern-1pt}<{\kern-1pt}r_{0}$
. This completes the proof of the lemma.
For each
![]() $x\in \Lambda $
and sufficiently small
$x\in \Lambda $
and sufficiently small
![]() $0<r<r_0$
, let
$0<r<r_0$
, let
 $$ \begin{align*} n_{1}=\min \bigg\{n\in{\mathbb{Z}}^{+}: C_{2} r \exp \bigg\{2(n+1) \delta-\sum_{i=0}^{n} \phi_{u}(f^{i} x)\bigg\} \geqslant r_{0}\bigg\}, \end{align*} $$
$$ \begin{align*} n_{1}=\min \bigg\{n\in{\mathbb{Z}}^{+}: C_{2} r \exp \bigg\{2(n+1) \delta-\sum_{i=0}^{n} \phi_{u}(f^{i} x)\bigg\} \geqslant r_{0}\bigg\}, \end{align*} $$
 $$ \begin{align*} n_{2}=\min \bigg\{n\in{\mathbb{Z}}^{+}: C_{2} r \exp \bigg\{2(n+1) \delta-\sum_{i=0}^{n} \phi_{s}(f^{-i} x)\bigg\} \geqslant r_{0}\bigg\}. \end{align*} $$
$$ \begin{align*} n_{2}=\min \bigg\{n\in{\mathbb{Z}}^{+}: C_{2} r \exp \bigg\{2(n+1) \delta-\sum_{i=0}^{n} \phi_{s}(f^{-i} x)\bigg\} \geqslant r_{0}\bigg\}. \end{align*} $$
It follows from the definition of
![]() $n_1,~n_2$
that
$n_1,~n_2$
that
![]() $n_1,n_2\rightarrow +\infty ~ (r\rightarrow 0)$
. Recall that
$n_1,n_2\rightarrow +\infty ~ (r\rightarrow 0)$
. Recall that
![]() $\mathcal {R}=\{R_{1}, \ldots , R_{s}\}$
is a Markov partition of
$\mathcal {R}=\{R_{1}, \ldots , R_{s}\}$
is a Markov partition of
![]() $\Lambda $
and
$\Lambda $
and
![]() $e_0$
is defined in equation (3.4).
$e_0$
is defined in equation (3.4).
Lemma 3.3. For each
![]() $x\in \Lambda $
, take a sufficiently small
$x\in \Lambda $
, take a sufficiently small
![]() $0<r<r_0$
so that
$0<r<r_0$
so that
![]() $n_1,~n_2>L$
. Then there exist
$n_1,~n_2>L$
. Then there exist
![]() $W_{1}, \ldots , W_{m} \in \mathcal {R}(-n_{2}, n_{1})$
with
$W_{1}, \ldots , W_{m} \in \mathcal {R}(-n_{2}, n_{1})$
with
![]() $m=m(x, r_{0},-n_{2}, n_{1}) \leq s^{2} e_{0}$
such that
$m=m(x, r_{0},-n_{2}, n_{1}) \leq s^{2} e_{0}$
such that
and
![]() $ B_{r}(x) \cap \Lambda \subset \bigcup _{k=1}^{m} W_{k}$
.
$ B_{r}(x) \cap \Lambda \subset \bigcup _{k=1}^{m} W_{k}$
.
Proof. For
![]() $y\in \Lambda $
, let
$y\in \Lambda $
, let
![]() $\mathcal {R}_{y}=\{Q \in \mathcal {R} \mid R \cap Q \neq \varnothing , y \in R \in \mathcal {R}\}$
and
$\mathcal {R}_{y}=\{Q \in \mathcal {R} \mid R \cap Q \neq \varnothing , y \in R \in \mathcal {R}\}$
and
![]() $P_y=\bigcup _{\mathcal {R}_{y}} Q$
, then
$P_y=\bigcup _{\mathcal {R}_{y}} Q$
, then
![]() $P_{y} \subset B_{2 \varepsilon _{0}}(y) \cap \Lambda $
. From the definition of
$P_{y} \subset B_{2 \varepsilon _{0}}(y) \cap \Lambda $
. From the definition of
![]() $\delta _{0}$
, if
$\delta _{0}$
, if
![]() $z \in \Lambda $
and
$z \in \Lambda $
and
![]() $d(y, z)<\delta _{0}$
, then for any
$d(y, z)<\delta _{0}$
, then for any
![]() $Q\in \mathcal {R}$
containing z,
$Q\in \mathcal {R}$
containing z,
![]() $Q \in \mathcal {R}_{y}$
.
$Q \in \mathcal {R}_{y}$
.
Let
 $$ \begin{align*} &\mathcal{P}(x,-n_{2}, n_{1})\\&\quad=\bigg\{W=\bigcap_{j=-n_{2}}^{n_1} f^{-j} R_{a_j} \in \mathcal{R}(-n_{2}, n_{1}) : R_{a_j} \subset P_{f^{j} x}~\text{ for all } j=-n_{2},\ldots, n_{1}\bigg\} \end{align*} $$
$$ \begin{align*} &\mathcal{P}(x,-n_{2}, n_{1})\\&\quad=\bigg\{W=\bigcap_{j=-n_{2}}^{n_1} f^{-j} R_{a_j} \in \mathcal{R}(-n_{2}, n_{1}) : R_{a_j} \subset P_{f^{j} x}~\text{ for all } j=-n_{2},\ldots, n_{1}\bigg\} \end{align*} $$
and
![]() $ \mathcal {P}(x, r_{0},-n_{2}, n_{1})=\{W \in \mathcal {P}(x,-n_{2}, n_{1}): B_{r_{0}}^{f}(x,-n_{2}, n_{1}) \cap W \neq \varnothing \}$
. By Lemma 3.2 and the choice of
$ \mathcal {P}(x, r_{0},-n_{2}, n_{1})=\{W \in \mathcal {P}(x,-n_{2}, n_{1}): B_{r_{0}}^{f}(x,-n_{2}, n_{1}) \cap W \neq \varnothing \}$
. By Lemma 3.2 and the choice of
![]() $n_1,n_2$
, we have
$n_1,n_2$
, we have
 $$ \begin{align*} B_r(x) \cap \Lambda\subset B_{r_{0}}^{f}(x,-n_{2}, n_{1}) \cap \Lambda\subset \bigcup_{W \in \mathcal{P}(x,r_0,-n_{2}, n_{1})} W. \end{align*} $$
$$ \begin{align*} B_r(x) \cap \Lambda\subset B_{r_{0}}^{f}(x,-n_{2}, n_{1}) \cap \Lambda\subset \bigcup_{W \in \mathcal{P}(x,r_0,-n_{2}, n_{1})} W. \end{align*} $$
Let
![]() $m=\#\mathcal {P}(x, r_{0},-n_{2}, n_{1})$
and
$m=\#\mathcal {P}(x, r_{0},-n_{2}, n_{1})$
and
![]() $\mathcal {P}(x, r_{0},-n_{2}, n_{1})=\{W_{1}, \ldots , W_{m}\}$
. To complete the proof of the lemma, it suffices to show that
$\mathcal {P}(x, r_{0},-n_{2}, n_{1})=\{W_{1}, \ldots , W_{m}\}$
. To complete the proof of the lemma, it suffices to show that
To prove this, set
![]() $\ell _{1}=\# \mathcal {R}_{f^{n_1} x},~~ \ell _{2}=\# \mathcal {R}_{f^{-n_2} x}$
and take
$\ell _{1}=\# \mathcal {R}_{f^{n_1} x},~~ \ell _{2}=\# \mathcal {R}_{f^{-n_2} x}$
and take
![]() $\alpha _{1}, \ldots , \alpha _{\ell _1}, \beta _{1}, \ldots , \beta _{\ell _{2}} \in \{1, \ldots , s\}$
so that
$\alpha _{1}, \ldots , \alpha _{\ell _1}, \beta _{1}, \ldots , \beta _{\ell _{2}} \in \{1, \ldots , s\}$
so that
 $$ \begin{align*}P_{f^{n_1} x}=\bigcup_{p=1}^{\ell_1} R_{\alpha_{p}},\quad P_{f^{-n_2} x}=\bigcup_{q=1}^{\ell_2} R_{\beta_{q}}.\end{align*} $$
$$ \begin{align*}P_{f^{n_1} x}=\bigcup_{p=1}^{\ell_1} R_{\alpha_{p}},\quad P_{f^{-n_2} x}=\bigcup_{q=1}^{\ell_2} R_{\beta_{q}}.\end{align*} $$
Then,
 $$ \begin{align*}\mathcal{P}(x, r_{0},-n_{2}, n_{1})=\bigcup_{p=1}^{l_1}\ \bigcup_{q=1}^{l_2} Q_{p, q},\end{align*} $$
$$ \begin{align*}\mathcal{P}(x, r_{0},-n_{2}, n_{1})=\bigcup_{p=1}^{l_1}\ \bigcup_{q=1}^{l_2} Q_{p, q},\end{align*} $$
where
![]() $Q_{p, q}=\{W \in \mathcal {P}(x, r_{0},-n_{2}, n_{1}):W \subset f^{n_{2}} R_{\beta _{q}} \cap f^{-n_{1}} R_{\alpha _{p}}\}$
. Fix
$Q_{p, q}=\{W \in \mathcal {P}(x, r_{0},-n_{2}, n_{1}):W \subset f^{n_{2}} R_{\beta _{q}} \cap f^{-n_{1}} R_{\alpha _{p}}\}$
. Fix
![]() $1 \leqslant p \leqslant \ell _{1}, 1 \leqslant q \leqslant \ell _{2}$
such that
$1 \leqslant p \leqslant \ell _{1}, 1 \leqslant q \leqslant \ell _{2}$
such that
![]() $Q_{p, q} \neq \varnothing $
. Put
$Q_{p, q} \neq \varnothing $
. Put
![]() $t=\# Q_{p, q}$
and let
$t=\# Q_{p, q}$
and let
Since
![]() $(\Sigma _{A},\sigma )$
is topologically mixing, there is a
$(\Sigma _{A},\sigma )$
is topologically mixing, there is a
![]() $K_0\geqslant 2$
such that
$K_0\geqslant 2$
such that
![]() $A^{K}>0$
for each
$A^{K}>0$
for each
![]() $K\geqslant K_0$
. We choose
$K\geqslant K_0$
. We choose
![]() $(\alpha _{p} \omega _{1} \omega _{2} \ldots \omega _{K_{0}-1} \beta _{q}) \in \Sigma (K_{0}+1)$
and take
$(\alpha _{p} \omega _{1} \omega _{2} \ldots \omega _{K_{0}-1} \beta _{q}) \in \Sigma (K_{0}+1)$
and take
 $$ \begin{align*}z_{p, q}^i\in W_{p, q}^{i} \cap\bigg(\bigcap_{k=1}^{K_{0}-1} f^{-n_{1}-k} R_{\omega_{k}}\bigg)\quad\text{such that }f^{n_{1}+n_{2}+K_{0}} z_{p, q}^{i}=z_{p, q}^{i}\end{align*} $$
$$ \begin{align*}z_{p, q}^i\in W_{p, q}^{i} \cap\bigg(\bigcap_{k=1}^{K_{0}-1} f^{-n_{1}-k} R_{\omega_{k}}\bigg)\quad\text{such that }f^{n_{1}+n_{2}+K_{0}} z_{p, q}^{i}=z_{p, q}^{i}\end{align*} $$
for each
![]() $i=1,2, \ldots ,t$
.
$i=1,2, \ldots ,t$
.
Hence, for
![]() $1\le i,~j\le t$
, one has
$1\le i,~j\le t$
, one has
 $$ \begin{align*} d(f^{k} z_{p, q}^{i}, f^{k} z_{p,q}^{j}) &\leqslant d(f^{k} z_{p, q}^{i}, f^{k} x)+d(f^{k} x, f^{k} z_{p, q}^{j}) \\ & \leqslant 2 \varepsilon_{0}+2 \varepsilon_{0}\\ &<c \end{align*} $$
$$ \begin{align*} d(f^{k} z_{p, q}^{i}, f^{k} z_{p,q}^{j}) &\leqslant d(f^{k} z_{p, q}^{i}, f^{k} x)+d(f^{k} x, f^{k} z_{p, q}^{j}) \\ & \leqslant 2 \varepsilon_{0}+2 \varepsilon_{0}\\ &<c \end{align*} $$
for each
![]() $k=-n_2,\ldots ,0,\ldots ,n_1$
, where c is the expansive constant of f. Moreover, for
$k=-n_2,\ldots ,0,\ldots ,n_1$
, where c is the expansive constant of f. Moreover, for
![]() $k=1,\ldots ,K_0-1$
, we have that
$k=1,\ldots ,K_0-1$
, we have that
This implies that
![]() $d(f^{m} z_{p, q}^{i}, f^{m} z_{p, q}^{j})<c$
for every
$d(f^{m} z_{p, q}^{i}, f^{m} z_{p, q}^{j})<c$
for every
![]() $m\in \mathbb {Z}$
. Thus,
$m\in \mathbb {Z}$
. Thus,
![]() $z_{p, q}^{i}=z_{p, q}^{j}$
for each
$z_{p, q}^{i}=z_{p, q}^{j}$
for each
![]() $1\leqslant i,j\leqslant t$
. Hence, we have that
$1\leqslant i,j\leqslant t$
. Hence, we have that
 $$ \begin{align*}z_{p, q}^{1} \in \bigcap_{i=1}^{t} W_{p, q}^{i}=\bigcap_{W \in Q_{p, q}} W.\end{align*} $$
$$ \begin{align*}z_{p, q}^{1} \in \bigcap_{i=1}^{t} W_{p, q}^{i}=\bigcap_{W \in Q_{p, q}} W.\end{align*} $$
Furthermore, one has
![]() $\# Q_{p, q} \le e_{0}$
since
$\# Q_{p, q} \le e_{0}$
since
![]() $\#\{W \in \mathcal {R}(-n_{2}, n_{1}): z_{p, q}^{1} \in W\} \leqslant e_{0}$
. Hence, we have
$\#\{W \in \mathcal {R}(-n_{2}, n_{1}): z_{p, q}^{1} \in W\} \leqslant e_{0}$
. Hence, we have
 $$ \begin{align*} m &=\# \mathcal{P}(x, r_{0},-n_{2}, n_{1}) \\ &=\sum_{p=1}^{l_{1}} \sum_{q=1}^{l_2} \# Q_{p, q} \\ & \leqslant s^{2} e_0. \end{align*} $$
$$ \begin{align*} m &=\# \mathcal{P}(x, r_{0},-n_{2}, n_{1}) \\ &=\sum_{p=1}^{l_{1}} \sum_{q=1}^{l_2} \# Q_{p, q} \\ & \leqslant s^{2} e_0. \end{align*} $$
This completes the proof of the lemma.
Using the previous results, we proceed with the proof of Theorem B.
Proof of Theorem B
For every
![]() $x\in \text {supp}\mu ~(=R_1)$
and sufficiently small
$x\in \text {supp}\mu ~(=R_1)$
and sufficiently small
![]() $0<r<r_0$
, choose
$0<r<r_0$
, choose
![]() $n_1,~n_2>L\geqslant N(\delta )$
and
$n_1,~n_2>L\geqslant N(\delta )$
and
![]() $W_1,\ldots ,W_m\in \mathcal {R}(-n_2,n_1)$
with
$W_1,\ldots ,W_m\in \mathcal {R}(-n_2,n_1)$
with
![]() $m\leqslant s^2 e_0$
, as in Lemma 3.3. For each
$m\leqslant s^2 e_0$
, as in Lemma 3.3. For each
![]() $k=1, \ldots , m$
, pick
$k=1, \ldots , m$
, pick
By Lemma 3.1, we have
 $$ \begin{align*} \exp \bigg\{\sum_{i=0}^{n_{1}} \phi_{u}(f^{i} y_{k})\bigg\} \leq \exp \bigg\{(n_1+1)\delta+\sum_{i=0}^{n_1} \phi_{u}(f^{i} x)\bigg\} \end{align*} $$
$$ \begin{align*} \exp \bigg\{\sum_{i=0}^{n_{1}} \phi_{u}(f^{i} y_{k})\bigg\} \leq \exp \bigg\{(n_1+1)\delta+\sum_{i=0}^{n_1} \phi_{u}(f^{i} x)\bigg\} \end{align*} $$
and
 $$ \begin{align*} \exp \bigg\{\sum_{j=0}^{n_2} \phi_{s}(f^{-j} y_{k})\bigg\} \leqslant \exp \bigg\{(n_2+1)\delta+\sum_{j=0}^{n_{2}} \phi_{s}(f^{-j} x)\bigg\}. \end{align*} $$
$$ \begin{align*} \exp \bigg\{\sum_{j=0}^{n_2} \phi_{s}(f^{-j} y_{k})\bigg\} \leqslant \exp \bigg\{(n_2+1)\delta+\sum_{j=0}^{n_{2}} \phi_{s}(f^{-j} x)\bigg\}. \end{align*} $$
Furthermore, for each
![]() $k=1, \ldots , m$
, it follows from equation (3.5) that
$k=1, \ldots , m$
, it follows from equation (3.5) that
 $$ \begin{align*} \mu(W_{k}) &\leqslant C_{1}A_{n_1+1}B_{n_2+1} \exp\bigg\{\sum_{i=0}^{n_{1}} t_{u} \phi_{u}(f^{i} y_{k})+\sum_{j=0}^{n_{2}} t_s \phi_{s}(f^{-j} y_{k})\bigg\}\\[-3pt]&\leq C_{1}A_{n_1+1}B_{n_2+1} \exp \bigg\{(t_u (n_1+1)+t_s (n_2+1))\delta+\sum_{i=0}^{n_{1}}t_u \phi_{u}(f^{i} x)\\[-3pt]& \quad+\sum_{j=0}^{n_{2}}t_{s}\phi_{s}(f^{-j} x)\bigg\}\\[-3pt]&\leq C_{1}A_{n_1+1}B_{n_2+1} \exp \{3(t_{u}(n_{1}+1) +t_{s}(n_{2}+1)) \delta\}\\[-3pt]&\quad\cdot\exp \bigg\{-2t_{u}(n_{1}+1) \delta+\sum_{i=0}^{n_{1}} t_u \phi_{u}(f^{i} x)-2t_{s}(n_{2}+1) \delta+\sum_{j=0}^{n_{2}} t_{s} \phi_{s}(f^{-j} x)\bigg\}\\[-3pt]&\leqslant C_{1}A_{n_1+1}B_{n_2+1}\bigg(\frac{C_{2} r}{r_{0}}\bigg)^{\dim_{H} \Lambda}\cdot \exp \{3(t_{u}(n_{1}+1) +t_{s}(n_{2}+1)) \delta\}, \end{align*} $$
$$ \begin{align*} \mu(W_{k}) &\leqslant C_{1}A_{n_1+1}B_{n_2+1} \exp\bigg\{\sum_{i=0}^{n_{1}} t_{u} \phi_{u}(f^{i} y_{k})+\sum_{j=0}^{n_{2}} t_s \phi_{s}(f^{-j} y_{k})\bigg\}\\[-3pt]&\leq C_{1}A_{n_1+1}B_{n_2+1} \exp \bigg\{(t_u (n_1+1)+t_s (n_2+1))\delta+\sum_{i=0}^{n_{1}}t_u \phi_{u}(f^{i} x)\\[-3pt]& \quad+\sum_{j=0}^{n_{2}}t_{s}\phi_{s}(f^{-j} x)\bigg\}\\[-3pt]&\leq C_{1}A_{n_1+1}B_{n_2+1} \exp \{3(t_{u}(n_{1}+1) +t_{s}(n_{2}+1)) \delta\}\\[-3pt]&\quad\cdot\exp \bigg\{-2t_{u}(n_{1}+1) \delta+\sum_{i=0}^{n_{1}} t_u \phi_{u}(f^{i} x)-2t_{s}(n_{2}+1) \delta+\sum_{j=0}^{n_{2}} t_{s} \phi_{s}(f^{-j} x)\bigg\}\\[-3pt]&\leqslant C_{1}A_{n_1+1}B_{n_2+1}\bigg(\frac{C_{2} r}{r_{0}}\bigg)^{\dim_{H} \Lambda}\cdot \exp \{3(t_{u}(n_{1}+1) +t_{s}(n_{2}+1)) \delta\}, \end{align*} $$
where we use the fact that
![]() $\dim _H\Lambda =t_u+t_s$
. Hence, we have
$\dim _H\Lambda =t_u+t_s$
. Hence, we have
 $$ \begin{align} \begin{split} \mu&(B_{r}(x) \cap \Lambda) \\ &\leqslant \sum_{k=1}^{m} \mu(W_{k})\\ &\leqslant CA_{n_1+1}B_{n_2+1}r^{\dim_H \Lambda} \cdot \exp \{3(t_{u}(n_{1}+1) +t_{s}(n_{2}+1)) \delta\}, \end{split} \end{align} $$
$$ \begin{align} \begin{split} \mu&(B_{r}(x) \cap \Lambda) \\ &\leqslant \sum_{k=1}^{m} \mu(W_{k})\\ &\leqslant CA_{n_1+1}B_{n_2+1}r^{\dim_H \Lambda} \cdot \exp \{3(t_{u}(n_{1}+1) +t_{s}(n_{2}+1)) \delta\}, \end{split} \end{align} $$
where
![]() $C=s^{2} e_{0}C_{1} C_{2}^{\operatorname {dim} _H \Lambda }r_{0}^{-\operatorname {dim} _H \Lambda }.$
$C=s^{2} e_{0}C_{1} C_{2}^{\operatorname {dim} _H \Lambda }r_{0}^{-\operatorname {dim} _H \Lambda }.$
By the definition of
![]() $n_1,~n_2$
, we have
$n_1,~n_2$
, we have
 $$ \begin{align} &2n_{1} \delta-\sum_{i=0}^{n_1-1} \phi_u(f^{i} x)<\log r_{0}-\log C_{2}-\log r, \end{align} $$
$$ \begin{align} &2n_{1} \delta-\sum_{i=0}^{n_1-1} \phi_u(f^{i} x)<\log r_{0}-\log C_{2}-\log r, \end{align} $$
 $$ \begin{align} &2n_{2} \delta-\sum_{i=0}^{n_2-1} \phi_{s}(f^{-i} x)<\log r_{0}-\log C_{2}-\log r. \end{align} $$
$$ \begin{align} &2n_{2} \delta-\sum_{i=0}^{n_2-1} \phi_{s}(f^{-i} x)<\log r_{0}-\log C_{2}-\log r. \end{align} $$
Let
![]() $ M:=\max _{x \in \Lambda }\{\phi _{u}(x), \phi _s (x)\}<0$
. Thus, by equation (3.7), we conclude
$ M:=\max _{x \in \Lambda }\{\phi _{u}(x), \phi _s (x)\}<0$
. Thus, by equation (3.7), we conclude
that is,
Similarly, by equatoin (3.8), one has
Therefore, by equation (3.6), we have
for every
![]() $x\in \text {supp}\mu $
. The arbitrariness of
$x\in \text {supp}\mu $
. The arbitrariness of
![]() $\delta $
implies
$\delta $
implies
for every
![]() $x\in \text {supp}\mu $
. Thus, we have that
$x\in \text {supp}\mu $
. Thus, we have that
However, the reverse inequality
![]() $\dim _{H} \mu \leqslant \dim _{H} \Lambda $
clearly follows from the definitions. This completes the proof of Theorem B.
$\dim _{H} \mu \leqslant \dim _{H} \Lambda $
clearly follows from the definitions. This completes the proof of Theorem B.
3.3 Proof of Theorem C
Assume that
![]() $f:M\rightarrow M$
is a
$f:M\rightarrow M$
is a
![]() $C^{1+\alpha }$
diffeomorphism on an
$C^{1+\alpha }$
diffeomorphism on an
![]() $m_0$
-dimensional compact Riemannian manifold, and let
$m_0$
-dimensional compact Riemannian manifold, and let
![]() $\Lambda \subset M$
be a compact locally maximal hyperbolic set such that
$\Lambda \subset M$
be a compact locally maximal hyperbolic set such that
![]() $f|_{\Lambda }$
is topologically mixing and average conformal. Recall that
$f|_{\Lambda }$
is topologically mixing and average conformal. Recall that
![]() $\mathcal {M}(f|_\Lambda )$
and
$\mathcal {M}(f|_\Lambda )$
and
![]() $\mathcal {E}(f|_\Lambda )$
denote the set of f-invariant measures and ergodic measures on
$\mathcal {E}(f|_\Lambda )$
denote the set of f-invariant measures and ergodic measures on
![]() $\Lambda $
, respectively.
$\Lambda $
, respectively.
Recall that the topological pressure
![]() $P(\phi )$
of a continuous function
$P(\phi )$
of a continuous function
![]() $\phi :\Lambda \mapsto \mathbb {R}$
(with respect to
$\phi :\Lambda \mapsto \mathbb {R}$
(with respect to
![]() $f|_{\Lambda }$
) satisfies the following variational principle:
$f|_{\Lambda }$
) satisfies the following variational principle:
 $$ \begin{align} P(\phi)=\sup _{\mu \in \mathcal{M}(f|_\Lambda)}\bigg\{h_{\mu}(f)+\int \phi ~d \mu\bigg\}. \end{align} $$
$$ \begin{align} P(\phi)=\sup _{\mu \in \mathcal{M}(f|_\Lambda)}\bigg\{h_{\mu}(f)+\int \phi ~d \mu\bigg\}. \end{align} $$
Remark that
![]() $P(0)=h_{\text {top}}(f)$
is the topological entropy of
$P(0)=h_{\text {top}}(f)$
is the topological entropy of
![]() $f|_{\Lambda }$
. A measure
$f|_{\Lambda }$
. A measure
![]() $\mu \in \mathcal {M}(f|_\Lambda )$
which attains the supermum in equation (3.9) is called an equilibrium measure of
$\mu \in \mathcal {M}(f|_\Lambda )$
which attains the supermum in equation (3.9) is called an equilibrium measure of
![]() $\phi $
, and two functions
$\phi $
, and two functions
![]() $\phi , \psi :\Lambda \rightarrow \mathbb {R}$
are said to be cohomologous if
$\phi , \psi :\Lambda \rightarrow \mathbb {R}$
are said to be cohomologous if
![]() $\phi -\psi =\eta -\eta \circ f$
for some continuous function
$\phi -\psi =\eta -\eta \circ f$
for some continuous function
![]() $\eta : \Lambda \rightarrow \mathbb {R}$
. Denote by
$\eta : \Lambda \rightarrow \mathbb {R}$
. Denote by
![]() $C^{\alpha }(\Lambda )$
the space of Hölder continuous functions
$C^{\alpha }(\Lambda )$
the space of Hölder continuous functions
![]() $\varphi :\Lambda \rightarrow \mathbb {R}$
with Hölder exponent
$\varphi :\Lambda \rightarrow \mathbb {R}$
with Hölder exponent
![]() $\alpha $
. We list several properties of the topological pressure in the following (see [Reference Ruelle23] for details):
$\alpha $
. We list several properties of the topological pressure in the following (see [Reference Ruelle23] for details):
-
(1) the map
 $\phi \mapsto P(\phi )$
is analytic in
$\phi \mapsto P(\phi )$
is analytic in
 $C^{\alpha }(\Lambda )$
;
$C^{\alpha }(\Lambda )$
; -
(2) each function
 $\phi \in C^{\alpha }(\Lambda )$
has a unique equilibrium measure
$\phi \in C^{\alpha }(\Lambda )$
has a unique equilibrium measure
 $\nu _{\phi } \in \mathcal {E}(f|_\Lambda )$
;
$\nu _{\phi } \in \mathcal {E}(f|_\Lambda )$
; -
(3) for each
 $\phi ,\psi \in C^{\alpha }(\Lambda )$
, we have
$\phi ,\psi \in C^{\alpha }(\Lambda )$
, we have
 $\nu _{\phi }=\nu _{\psi }$
if and only if
$\nu _{\phi }=\nu _{\psi }$
if and only if
 $\phi -\psi $
is cohomologous to a constant;
$\phi -\psi $
is cohomologous to a constant; -
(4) for each
 $\phi ,\psi \in C^{\alpha }(\Lambda )$
and
$\phi ,\psi \in C^{\alpha }(\Lambda )$
and
 $t\in \mathbb {R}$
, we have with equality if and only if
$t\in \mathbb {R}$
, we have with equality if and only if $$ \begin{align*}\frac{d}{d t} P(\phi+t \psi) \geqslant 0,\end{align*} $$
$$ \begin{align*}\frac{d}{d t} P(\phi+t \psi) \geqslant 0,\end{align*} $$
 $\psi $
is cohomologous to a constant.
$\psi $
is cohomologous to a constant.
Note that the functions
![]() $\phi _u$
and
$\phi _u$
and
![]() $\phi _s$
defined in equation (3.1) are
$\phi _s$
defined in equation (3.1) are
![]() $\alpha $
-Hölder continuous in this case. For each
$\alpha $
-Hölder continuous in this case. For each
![]() $\nu \in \mathcal {M}(f|_\Lambda )$
, put
$\nu \in \mathcal {M}(f|_\Lambda )$
, put
 $$ \begin{align*}\unicode{x3bb}_{u}(\nu)=-\int \phi_{u}~ d \nu,~~\unicode{x3bb}_{s}(\nu)=\int \phi_{s}~ d \nu \quad\text{and}\quad d(\nu)=h_{\nu}(f)\bigg(\frac{1}{\unicode{x3bb}_{u}(\nu)}-\frac{1}{\unicode{x3bb}_{s}(\nu)}\bigg),\end{align*} $$
$$ \begin{align*}\unicode{x3bb}_{u}(\nu)=-\int \phi_{u}~ d \nu,~~\unicode{x3bb}_{s}(\nu)=\int \phi_{s}~ d \nu \quad\text{and}\quad d(\nu)=h_{\nu}(f)\bigg(\frac{1}{\unicode{x3bb}_{u}(\nu)}-\frac{1}{\unicode{x3bb}_{s}(\nu)}\bigg),\end{align*} $$
then
![]() $\unicode{x3bb} _{u}(\nu )>0,~ \unicode{x3bb} _{s}(\nu )<0$
. Furthermore, if
$\unicode{x3bb} _{u}(\nu )>0,~ \unicode{x3bb} _{s}(\nu )<0$
. Furthermore, if
![]() $\nu \in \mathcal {E}(f|_\Lambda )$
, then
$\nu \in \mathcal {E}(f|_\Lambda )$
, then
See [Reference Wang and Cao28] for the detailed proofs, which can be viewed as an extension of Young’s results in [Reference Young31] to the case of an average conformal hyperbolic setting. If
![]() $\mu \in \mathcal {M}(f|_\Lambda )$
, Fang, Cao, and Zhao [Reference Fang, Cao and Zhao16, Theorem 4.4] proved that
$\mu \in \mathcal {M}(f|_\Lambda )$
, Fang, Cao, and Zhao [Reference Fang, Cao and Zhao16, Theorem 4.4] proved that
with the essential supremum taken with respect to the ergodic decomposition
![]() $\tau $
of
$\tau $
of
![]() $\mu $
. See [Reference Barreira and Wolf6, Theorem 2] for the case of hyperbolic surface diffeomorphisms. Their approach extends without change to general conformal hyperbolic diffeomorphisms (see [Reference Barreira4, Theorem 13.2.4]). Consequently, to prove Theorem C, it suffices to show that there exists
$\mu $
. See [Reference Barreira and Wolf6, Theorem 2] for the case of hyperbolic surface diffeomorphisms. Their approach extends without change to general conformal hyperbolic diffeomorphisms (see [Reference Barreira4, Theorem 13.2.4]). Consequently, to prove Theorem C, it suffices to show that there exists
![]() $\mu \in \mathcal {E}(f|_\Lambda )$
so that
$\mu \in \mathcal {E}(f|_\Lambda )$
so that
Next, one can show the desired result by following mutatis mutandis Barreira and Wolf’s proof [Reference Barreira and Wolf5] (see also [Reference Barreira4, Ch. 5]). We outline some key steps for the reader’s convenience.
Consider the following bivariate function:
Since
![]() $\phi _{u}$
,
$\phi _{u}$
,
![]() $\phi _{s}\in C^{\alpha }(\Lambda )$
,
$\phi _{s}\in C^{\alpha }(\Lambda )$
,
![]() $p \phi _{u}+q \phi _{s}$
has a unique equilibrium measure
$p \phi _{u}+q \phi _{s}$
has a unique equilibrium measure
![]() $\nu _{p,q} \in \mathcal {E}(f|_\Lambda )$
for each
$\nu _{p,q} \in \mathcal {E}(f|_\Lambda )$
for each
![]() $(p, q) \in \mathbb {R}^{2}$
. Let
$(p, q) \in \mathbb {R}^{2}$
. Let
and
![]() $Q(p, q)=h(p, q)-p \unicode{x3bb} _{u}(p, q)+q \unicode{x3bb} _{s}(p, q)$
. By properties (1)–(4) of the topological pressure, one can show
$Q(p, q)=h(p, q)-p \unicode{x3bb} _{u}(p, q)+q \unicode{x3bb} _{s}(p, q)$
. By properties (1)–(4) of the topological pressure, one can show
![]() $\unicode{x3bb} _{u},\unicode{x3bb} _{s}$
and h as functions in
$\unicode{x3bb} _{u},\unicode{x3bb} _{s}$
and h as functions in
![]() $\mathbb {R}^{2}$
are real-analytic. Furthermore, let
$\mathbb {R}^{2}$
are real-analytic. Furthermore, let
Then
![]() $d_s$
and
$d_s$
and
![]() $d_u$
are also real-analytic.
$d_u$
are also real-analytic.
Since the maps
![]() $\nu \mapsto \unicode{x3bb} _{u} (\nu )$
and
$\nu \mapsto \unicode{x3bb} _{u} (\nu )$
and
![]() $\nu \mapsto \unicode{x3bb} _{s} (\nu )$
are continuous on the compact space
$\nu \mapsto \unicode{x3bb} _{s} (\nu )$
are continuous on the compact space
![]() $\mathcal {M}(f|_\Lambda )$
, put
$\mathcal {M}(f|_\Lambda )$
, put
 $$ \begin{align} \unicode{x3bb}_{u}^{\min }=\min_{\mu\in\mathcal{M}(f|_\Lambda)} \unicode{x3bb}_{u}(\mu),\quad\unicode{x3bb}_{u}^{\max }=\max_{\mu\in\mathcal{M}(f|_\Lambda)} \unicode{x3bb}_{u}(\mu),\nonumber\\ \unicode{x3bb}_{s}^{\min }=\min_{\mu\in\mathcal{M}(f|_\Lambda)} \unicode{x3bb}_{s}(\mu),\quad\unicode{x3bb}_{s}^{\max }=\max_{\mu\in\mathcal{M}(f|_\Lambda)} \unicode{x3bb}_{s}(\mu). \end{align} $$
$$ \begin{align} \unicode{x3bb}_{u}^{\min }=\min_{\mu\in\mathcal{M}(f|_\Lambda)} \unicode{x3bb}_{u}(\mu),\quad\unicode{x3bb}_{u}^{\max }=\max_{\mu\in\mathcal{M}(f|_\Lambda)} \unicode{x3bb}_{u}(\mu),\nonumber\\ \unicode{x3bb}_{s}^{\min }=\min_{\mu\in\mathcal{M}(f|_\Lambda)} \unicode{x3bb}_{s}(\mu),\quad\unicode{x3bb}_{s}^{\max }=\max_{\mu\in\mathcal{M}(f|_\Lambda)} \unicode{x3bb}_{s}(\mu). \end{align} $$
Set
Note that
![]() $I_{u}\neq \varnothing $
(respectively
$I_{u}\neq \varnothing $
(respectively
![]() $I_{s}\neq \varnothing $
) if and only if
$I_{s}\neq \varnothing $
) if and only if
![]() $\phi _{u}$
(respectively
$\phi _{u}$
(respectively
![]() $\phi _{s}$
) is not cohomologous to a constant.
$\phi _{s}$
) is not cohomologous to a constant.
Let
![]() $\{\nu _{n}\}_{n\geqslant 1}$
be a sequence of measures in
$\{\nu _{n}\}_{n\geqslant 1}$
be a sequence of measures in
![]() $\mathcal {E}(f|_\Lambda )$
such that
$\mathcal {E}(f|_\Lambda )$
such that
Without loss of generality, assume that
![]() $\{\nu _{n}\}_{n\geqslant 1}$
converges to some measure
$\{\nu _{n}\}_{n\geqslant 1}$
converges to some measure
![]() $m \in \mathcal {M}(f|_\Lambda )$
. By equation (3.10) and the upper semi-continuity of the entropy map
$m \in \mathcal {M}(f|_\Lambda )$
. By equation (3.10) and the upper semi-continuity of the entropy map
![]() $\nu \mapsto h_{\nu }(f)$
, one has
$\nu \mapsto h_{\nu }(f)$
, one has
To prove the desired result, it suffices to show that there exists
![]() $\mu \in \mathcal {E}(f|_\Lambda )$
such that
$\mu \in \mathcal {E}(f|_\Lambda )$
such that
We also note that when m is ergodic, it follows from equation (3.10) that
![]() $\dim _{H}m=d(m)$
, this completes the proof. However, m may be non-ergodic.
$\dim _{H}m=d(m)$
, this completes the proof. However, m may be non-ergodic.
As in [Reference Barreira4, Lemmas 5.24, 5.25, and 5.26], one can show the following properties:
-
(i) if
 $\unicode{x3bb} _{s}(m) \in I_{s}$
, then there exists
$\unicode{x3bb} _{s}(m) \in I_{s}$
, then there exists
 ${p \in [0, {h_{m}(f)}/{\unicode{x3bb} _{u}(m)}]}$
such that
${p \in [0, {h_{m}(f)}/{\unicode{x3bb} _{u}(m)}]}$
such that
 $\unicode{x3bb} _{u}(p, \gamma _{s}(p))=\unicode{x3bb} _{u}(m);$
$\unicode{x3bb} _{u}(p, \gamma _{s}(p))=\unicode{x3bb} _{u}(m);$
-
(ii) assume that neither
 $\phi _{u}$
nor
$\phi _{u}$
nor
 $\phi _{s}$
are cohomologous to a constant, then
$\phi _{s}$
are cohomologous to a constant, then
 $\unicode{x3bb} _u(m)\in I_u \text { if and only if }\unicode{x3bb} _s(m)\in I_s$
;
$\unicode{x3bb} _u(m)\in I_u \text { if and only if }\unicode{x3bb} _s(m)\in I_s$
; -
(iii) if
 $\unicode{x3bb} _{u}(p, q)=\unicode{x3bb} _{u}(m)\text { and }\unicode{x3bb} _{s}(p, q)=\unicode{x3bb} _{s}(m)$
for some
$\unicode{x3bb} _{u}(p, q)=\unicode{x3bb} _{u}(m)\text { and }\unicode{x3bb} _{s}(p, q)=\unicode{x3bb} _{s}(m)$
for some
 $p, q\in \mathbb {R}$
, then
$p, q\in \mathbb {R}$
, then
 $m=\nu _{p,q}$
.
$m=\nu _{p,q}$
.
Item (ii) implies that it is sufficient to consider the following four cases:
-
(I)
 $\unicode{x3bb} _u(m)\in I_u \text { and }\unicode{x3bb} _s(m)\in I_s;$
$\unicode{x3bb} _u(m)\in I_u \text { and }\unicode{x3bb} _s(m)\in I_s;$
-
(II)
 $\unicode{x3bb} _s(m)\in I_s$
and
$\unicode{x3bb} _s(m)\in I_s$
and
 $\phi _{u}$
is cohomologous to a constant;
$\phi _{u}$
is cohomologous to a constant; -
(III)
 $\unicode{x3bb} _u(m)\in I_u$
and
$\unicode{x3bb} _u(m)\in I_u$
and
 $\phi _{s}$
is cohomologous to a constant;
$\phi _{s}$
is cohomologous to a constant; -
(IV)
 $\unicode{x3bb} _u(m)\notin I_u $
and
$\unicode{x3bb} _u(m)\notin I_u $
and
 $\unicode{x3bb} _s(m)\notin I_s.$
$\unicode{x3bb} _s(m)\notin I_s.$
For case (I), as in [Reference Barreira and Wolf5, Lemma 4], one can prove that there exists
![]() $(p,q)\in \mathbb {R}^2$
so that
$(p,q)\in \mathbb {R}^2$
so that
![]() $m=\nu _{p,q}$
. For cases (II) and (III), following the proof of [Reference Barreira and Wolf5, Lemmas 5 and 6], one can also show that
$m=\nu _{p,q}$
. For cases (II) and (III), following the proof of [Reference Barreira and Wolf5, Lemmas 5 and 6], one can also show that
![]() $m=\nu _{p,q}$
for some
$m=\nu _{p,q}$
for some
![]() $(p,q)\in \mathbb {R}^2$
. For the last case, one can show that: (1)
$(p,q)\in \mathbb {R}^2$
. For the last case, one can show that: (1)
![]() $\unicode{x3bb} _{u}(m)=\unicode{x3bb} _{u}^{\min } \text { and } \unicode{x3bb} _{s}(m)=\unicode{x3bb} _{s}^{\max }$
; (2) there exists
$\unicode{x3bb} _{u}(m)=\unicode{x3bb} _{u}^{\min } \text { and } \unicode{x3bb} _{s}(m)=\unicode{x3bb} _{s}^{\max }$
; (2) there exists
![]() $\nu \in \mathcal {E}(f|_\Lambda )$
such that
$\nu \in \mathcal {E}(f|_\Lambda )$
such that
This completes the proof of equation (3.12).
Acknowledgements
The authors are grateful to the anonymous referee for valuable comments which helped to improve the manuscript greatly. This work is partially supported by The National Key Research and Development Program of China (2022YFA1005802). Y.Z. is partially supported by NSFC (12271386) and Qinglan project of Jiangsu Province.