Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T12:46:31.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximally highly proximal flows

Part of: Set theory Connections with other structures, applications Topological dynamics

Published online by Cambridge University Press:  18 May 2020

ANDY ZUCKER Open the ORCID record for ANDY ZUCKER [Opens in a new window]
ANDY ZUCKER*
Affiliation:
Université Paris Diderot, IMJ-PRG, 8 place Aurélie Nemours, Bat. Sophie Germain, Paris, 75205, France email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For 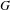$G$ a Polish group, we consider 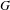$G$-flows which either contain a comeager orbit or have all orbits meager. We single out a class of flows, the maximally highly proximal (MHP) flows, for which this analysis is particularly nice. In the former case, we provide a complete structure theorem for flows containing comeager orbits, generalizing theorems of Melleray, Nguyen Van Thé, and Tsankov and of Ben Yaacov, Melleray, and Tsankov. In the latter, we show that any minimal MHP flow with all orbits meager has a metrizable factor with all orbits meager, thus ‘reflecting’ complicated dynamical behavior to metrizable flows. We then apply this to obtain a structure theorem for Polish groups whose universal minimal flow is distal.

Keywords

topological dynamicscomeager orbitshighly proximal extensions

MSC classification

Primary: 37B05: Transformations and group actions with special properties (minimality, distality, proximality, etc.)
Secondary: 54H20: Topological dynamics 03E15: Descriptive set theory
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 7 , July 2021 , pp. 2220 - 2240
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Angel, O., Kechris, A. S. and Lyons, R.. Random orderings and unique ergodicity of automorphism groups. J. Eur. Math. Soc. (JEMS) 16 (2014), 2059–2095.CrossRefGoogle Scholar
Auslander, J.. Minimal Flows and Their Extensions. North-Holland, Amsterdam, 1988.Google Scholar
Auslander, J. and Glasner, S.. Distal and highly proximal extensions of minimal flows. Indiana Univ. Math. J. 26(4) (1977), 731–749.CrossRefGoogle Scholar
Ben Yaacov, I.. Lipschitz functions on topometric spaces. J. Log. Anal. 5(8) (2013), 1–21.Google Scholar
Ben Yaacov, I., Berenstein, A., Henson, C. W. and Usvyatsov, A.. Model Theory for Metric Structures (Model Theory with Applications to Algebra and Analysis, 2, London Mathematical Society Lecture Note Series, 350) . Cambridge University Press, Cambridge, 2008, pp. 315–427.Google Scholar
Ben Yaacov, I. and Melleray, J.. Grey subsets of Polish spaces. J. Symb. Log. 80(4) (2015), 1379–1397.CrossRefGoogle Scholar
Ben Yaacov, I., Melleray, J. and Tsankov, T.. Metrizable universal minimal flows of Polish groups have a comeager orbit. Geom. Funct. Anal. 27(1) (2017), 67–77.CrossRefGoogle Scholar
Glasner, S.. Proximal Flows (Lecture Notes in Mathematics, 517) . Springer, Berlin, 1976.CrossRefGoogle Scholar
Kechris, A., Pestov, V. and Todorčević, S.. Fraïssé limits, Ramsey theory, and topological dynamics of automorphism groups. Geom. Funct. Anal. 15 (2005), 106–189.CrossRefGoogle Scholar
Kwiatkowska, A.. Universal minimal flows of generalized Ważewski dendrites. J. Symb. Log. 83(4) (2018), 1618–1632.CrossRefGoogle Scholar
Melleray, J., Nguyen Van Thé, L. and Tsankov, T.. Polish groups with metrizable universal minimal flow. Int. Math. Res. Not. IMRN 2016(5) (2016), 1285–1307.Google Scholar
Zucker, A.. Topological dynamics of automorphism groups, ultrafilter combinatorics, and the generic point problem. Trans. Amer. Math. Soc. 368(9) (2016), 6715–6740.CrossRefGoogle Scholar
Zucker, A.. A direct solution to the generic point problem. Proc. Amer. Math. Soc. 146(5) (2018), 2143–2148.CrossRefGoogle Scholar
Zucker, A.. New directions in the abstract topological dynamics of Polish groups. PhD Thesis, Carnegie Mellon University, 2018.Google Scholar