Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-26T20:37:11.108Z Has data issue: false hasContentIssue false
  • English
  • Français

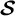$\mathcal{\textbf{S}}$-adic characterization of minimal ternary dendric shifts

Part of: Discrete mathematics in relation to computer science Topological dynamics

Published online by Cambridge University Press:  02 September 2021

FRANCE GHEERAERT ,
MARIE LEJEUNE  and
JULIEN LEROY Open the ORCID record for JULIEN LEROY [Opens in a new window]
FRANCE GHEERAERT
Affiliation:
Department of Mathematics, University of LiĂšge, LiĂšge, 4000, Belgium (e-mail: [email protected], [email protected])
MARIE LEJEUNE
Affiliation:
Department of Mathematics, University of LiĂšge, LiĂšge, 4000, Belgium (e-mail: [email protected], [email protected])
JULIEN LEROY*
Affiliation:
Department of Mathematics, University of LiĂšge, LiĂšge, 4000, Belgium (e-mail: [email protected], [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Dendric shifts are defined by combinatorial restrictions of the extensions of the words in their languages. This family generalizes well-known families of shifts such as Sturmian shifts, Arnoux–Rauzy shifts and codings of interval exchange transformations. It is known that any minimal dendric shift has a primitive 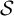$\mathcal {S}$ -adic representation where the morphisms in $\mathcal {S}$ are positive tame automorphisms of the free group generated by the alphabet. 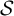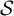In this paper, we investigate those $\mathcal {S}$ -adic representations, heading towards an 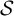$\mathcal {S}$ -adic characterization of this family. We obtain such a characterization in the ternary case, involving a directed graph with two vertices.

Keywords

symbolic dynamicssubstitutions𝒼-adicdendricinterval exchangereturn words

MSC classification

Primary: 37B10: Symbolic dynamics 68R15: Combinatorics on words
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 11 , November 2022 , pp. 3393 - 3432
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnoux, P. and Rauzy, G.. ReprĂ©sentation gĂ©omĂ©trique de suites de complexitĂ© $2n+1$ . Bull. Soc. Math. France 119(2) (1991), 199–215.CrossRefGoogle Scholar
Arnold, V. I.. Small denominators and problems of stability of motion in classical and celestial mechanics. Uspehi Mat. Nauk 18(114) (1963), 91–192.Google Scholar
BerthĂ©, V., Bernales, P. Cecchi, Durand, F., Leroy, J., Perrin, D. and Petite, S.. On the dimension group of unimodular $\mathcal{S}$ -adic subshifts. Monatsh. Math. 194(4) (2021), 687–717.CrossRefGoogle Scholar
BerthĂ©, V. and Delecroix, V.. Beyond substitutive dynamical systems: $\mathcal{S}$ -adic expansions. Numeration and substitution 2012 (RIMS KĂŽkyĂ»roku Bessatsu, B46). Research Institute for Mathematical Sciences (RIMS), Kyoto, 2014, pp. 81–123.Google Scholar
BerthĂ©, V., Dolce, F., Durand, F., Leroy, J. and Perrin, D.. Rigidity and substitutive dendric words. Internat. J. Found. Comput. Sci. 29(5) (2018), 705–720.CrossRefGoogle Scholar
BerthĂ©, V., De Felice, C., Dolce, F., Leroy, J., Perrin, D., Reutenauer, C. and Rindone, G.. Acyclic, connected and tree sets. Monatsh. Math. 176(4) (2015), 521–550.CrossRefGoogle Scholar
BerthĂ©, V., De Felice, C., Dolce, F., Leroy, J., Perrin, D., Reutenauer, C., and Rindone, G.. The finite index basis property. J. Pure Appl. Algebra 219(7) (2015), 2521–2537.CrossRefGoogle Scholar
BerthĂ©, V., De Felice, C., Dolce, F., Leroy, J., Perrin, D., Reutenauer, C. and Rindone, G.. Maximal bifix decoding. Discrete Math. 338(5) (2015), 725–742.CrossRefGoogle Scholar
BĂ©daride, N., Hilion, A., and Lustig, M.. Invariant measures on finite rank subshifts. Preprint, 2020, arXiv:2007.09700.Google Scholar
BĂ©daride, N., Hilion, A. and Lustig, M.. Tower power for $\mathcal{S}$ -adics. Math. Z. 297(3-4) (2021), 1853–1875.CrossRefGoogle Scholar
Boshernitzan, M.. A unique ergodicity of minimal symbolic flows with linear block growth. J. Anal. Math. 44 (1984/85), 77–96.CrossRefGoogle Scholar
Cassaigne, J., LabbĂ©, S. and Leroy, J.. A set of sequences of complexity $2n+1$ . Combinatorics on Words (Lecture Notes in Computer Science, 10432). Springer, Cham, 2017, pp. 144–156.CrossRefGoogle Scholar
Cassaigne, J., Labbé, S. and Leroy, J.. Almost everywhere balanced sequences of complexity $2n+1$ . Preprint, 2021, arXiv:2102.10093.Google Scholar
Cassaigne, J. and Nicolas, F.. Factor complexity. Combinatorics, Automata and Number Theory (Encyclopedia of Mathematics and its Applications, 135). Cambridge University Press, Cambridge, 2010, pp. 163–247.CrossRefGoogle Scholar
Donoso, S., Durand, F., Maass, A. and Petite, S.. Interplay between finite topological rank minimal cantor systems, $\mathbf{\mathcal{S}}$ -adic subshifts and their complexity Trans. Amer. Math. Soc. 374(5) (2021), 3453–3489.CrossRefGoogle Scholar
Delecroix, V.. Interval exchange transformations. Lecture Notes from the CIMPA Research School “Dynamics on Cantor Sets”, 2015, available at https://cantorsalta2015.sciencesconf.org/ conference/cantorsalta2015/Delecroix.pdf Google Scholar
Damron, M. and Fickenscher, J.. The number of ergodic measures for transitive subshifts under the regular bispecial condition. Ergod. Th. & Dynam. Sys. doi: 10.1017/etds.2020.134. Published online 29 December 2020.CrossRefGoogle Scholar
Durand, F., Leroy, J. and Richomme, G.. Do the properties of an $\mathcal{S}$ -adic representation determine factor complexity? J. Integer Seq. 16(2) (2013), Article 13.2.6, 30.Google Scholar
Dolce, F. and Perrin, D.. Interval exchanges, admissibility and branching rauzy induction. RAIRO-Theor. Inf. Appl. 51(3) (2017), 135–139.CrossRefGoogle Scholar
Durand, F.. Linearly recurrent subshifts have a finite number of non-periodic subshift factors. Ergod. Th. & Dynam. Sys. 20(4) (2000), 1061–1078.CrossRefGoogle Scholar
Durand, F.. A characterization of substitutive sequences using return words. Discrete Math. 179(1-3) (1998), 89–101.CrossRefGoogle Scholar
Espinoza, B. and Maass, A.. On the automorphism group of minimal s-adic subshifts of finite alphabet rank. Preprint, 2020. arXiv:2008.05996.CrossRefGoogle Scholar
Ferenczi, S.. Rank and symbolic complexity. Ergod. Th. & Dynam. Sys. 16(4) (1996), 663–682.CrossRefGoogle Scholar
Ferenczi, S. and Zamboni, L. Q.. Languages of $k$ -interval exchange transformations. Bull. Lond. Math. Soc. 40(4) (2008), 705–714.CrossRefGoogle Scholar
Keane, M.. Interval exchange transformations. Math. Z., 141 (1975), 25–31.CrossRefGoogle Scholar
Leroy, J.. Some improvements of the $\mathcal{S}$ -adic conjecture. Adv. Appl. Math. 48(1) (2012), 79–98.CrossRefGoogle Scholar
Leroy, J.. An $\mathcal{S}$ -adic characterization of minimal subshifts with first difference of complexity $1\le p\left(n+1\right)-p(n)\le 2$ . Discrete Math. Theor. Comput. Sci. 16(1) (2014), 233–286.Google Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.CrossRefGoogle Scholar
Oseledec, V. I.. The spectrum of ergodic automorphisms. Dokl. Akad. Nauk SSSR 168 (1966), 1009–1011.Google Scholar
Rauzy, G.. Échanges d’intervalles et transformations induites. Acta Arithm. 34(4) (1979), 315–328.CrossRefGoogle Scholar