Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T04:21:57.182Z Has data issue: false hasContentIssue false
  • English
  • Français

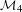${\mathcal{M}}_{4}$ is regular-closed

Published online by Cambridge University Press:  10 April 2018

YUTARO HIMEKI  and
YUTAKA ISHII
YUTARO HIMEKI
Affiliation:
Department of Mathematics, Kyushu University, Motooka, Fukuoka 819-0395, Japan email [email protected], [email protected]
YUTAKA ISHII
Affiliation:
Department of Mathematics, Kyushu University, Motooka, Fukuoka 819-0395, Japan email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For each 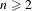$n\geq 2$, we investigate a family of iterated function systems which is parameterized by a common contraction ratio 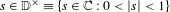$s\in \mathbb{D}^{\times }\equiv \{s\in \mathbb{C}:0<|s|<1\}$ and possesses a rotational symmetry of order $n$. Let 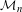${\mathcal{M}}_{n}$ be the locus of contraction ratio $s$ for which the corresponding self-similar set is connected. The purpose of this paper is to show that 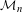${\mathcal{M}}_{n}$ is regular-closed, that is, 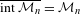$\overline{\text{int}\,{\mathcal{M}}_{n}}={\mathcal{M}}_{n}$ holds for 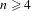$n\geq 4$. This gives a new result for 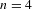$n=4$ and a simple geometric proof of the previously known result by Bandt and Hung [Fractal $n$-gons and their Mandelbrot sets. Nonlinearity 21 (2008), 2653–2670] for 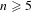$n\geq 5$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 1 , January 2020 , pp. 213 - 220
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bandt, C.. On the Mandelbrot set for pairs of linear maps. Nonlinearity 15(4) (2002), 1127–1147.10.1088/0951-7715/15/4/309Google Scholar
Bandt, C. and Hung, N. V.. Fractal n-gons and their Mandelbrot sets. Nonlinearity 21(11) (2008), 2653–2670.Google Scholar
Barnsley, M. and Harrington, A.. A Mandelbrot set for pairs of linear maps. Phys. D. 15(3) (1985), 421–432.10.1016/S0167-2789(85)80008-7Google Scholar
Bousch, T.. Paires de similitudes $z\rightarrow sz+1$ , $z\rightarrow sz-1$ . Preprint, 1988.Google Scholar
Bousch, T.. Connexité locale et par chemins hölderiens pour les systèmes itérés de fonctions. Preprint, 1992.Google Scholar
Calegari, D., Koch, S. and Walker, A.. Roots, Schottky semigroups, and a proof of Bandt’s conjecture. Ergod. Th. & Dynam. Sys. 37(8) (2017), 2487–2555.10.1017/etds.2016.17Google Scholar
Falconer, K.. Fractal Geometry. Mathematical Foundations and Applications. John Wiley & Sons, Chichester, 1990.Google Scholar
Hata, M.. On the structure of self-similar sets. Japan J. Appl. Math. 2(2) (1985), 381–414.10.1007/BF03167083Google Scholar