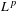 $L^{p}$ spectrum and heat dynamics of locally symmetric spaces of higher rank
$L^{p}$ spectrum and heat dynamics of locally symmetric spaces of higher rankPublished online by Cambridge University Press: 30 June 2014
The aim of this paper is to study the spectrum of the 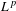 $L^{p}$ Laplacian and the dynamics of the
$L^{p}$ Laplacian and the dynamics of the 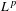 $L^{p}$ heat semigroup on non-compact locally symmetric spaces of higher rank. Our work here generalizes previously obtained results in the setting of locally symmetric spaces of rank one to higher rank spaces. Similarly as in the rank-one case, it turns out that the
$L^{p}$ heat semigroup on non-compact locally symmetric spaces of higher rank. Our work here generalizes previously obtained results in the setting of locally symmetric spaces of rank one to higher rank spaces. Similarly as in the rank-one case, it turns out that the 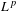 $L^{p}$ heat semigroup on
$L^{p}$ heat semigroup on 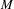 $M$ has a certain chaotic behavior if
$M$ has a certain chaotic behavior if 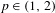 $p\in (1,2)$, whereas for
$p\in (1,2)$, whereas for 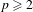 $p\geq 2$ such chaotic behavior never occurs.
$p\geq 2$ such chaotic behavior never occurs.