Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-27T03:59:30.377Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower bounds and the asymptotic behaviour of positive operator semigroups

Published online by Cambridge University Press:  02 May 2017

MORITZ GERLACH  and
JOCHEN GLÜCK
MORITZ GERLACH
Affiliation:
Universität Potsdam, Institut für Mathematik, Karl-Liebknecht-Straße 24–25, 14476 Potsdam, Germany email [email protected]
JOCHEN GLÜCK
Affiliation:
Institute of Applied Analysis, Ulm University, 89069 Ulm, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

If 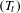$(T_{t})$ is a semigroup of Markov operators on an 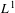$L^{1}$-space that admits a non-trivial lower bound, then a well-known theorem of Lasota and Yorke asserts that the semigroup is strongly convergent as 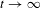$t\rightarrow \infty$. In this article we generalize and improve this result in several respects. First, we give a new and very simple proof for the fact that the same conclusion also holds if the semigroup is merely assumed to be bounded instead of Markov. As a main result, we then prove a version of this theorem for semigroups which only admit certain individual lower bounds. Moreover, we generalize a theorem of Ding on semigroups of Frobenius–Perron operators. We also demonstrate how our results can be adapted to the setting of general Banach lattices and we give some counterexamples to show optimality of our results. Our methods combine some rather concrete estimates and approximation arguments with abstract functional analytical tools. One of these tools is a theorem which relates the convergence of a time-continuous operator semigroup to the convergence of embedded discrete semigroups.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 8 , December 2018 , pp. 3012 - 3041
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arendt, W.. Positive semigroups of kernel operators. Positivity 12(1) (2008), 25–44.Google Scholar
Arendt, W., Batty, C. J. K., Hieber, M. and Neubrander, F.. Vector-valued Laplace Transforms and Cauchy Problems (Monographs in Mathematics, 96) , 2nd edn. Birkhäuser–Springer, Basel, 2011.Google Scholar
Arendt, W., Grabosch, A., Greiner, G., Groh, U., Lotz, H. P., Moustakas, U., Nagel, R., Neubrander, F. and Schlotterbeck, U.. One-parameter Semigroups of Positive Operators (Lecture Notes in Mathematics, 1184) . Springer, Berlin, 1986.Google Scholar
Bartoszek, W.. Asymptotic properties of the iterates of stochastic operators on (AL) Banach lattices. Ann. Polon. Math. 52(2) (1990), 165–173.Google Scholar
Bartoszek, W.. The work of Professor Andrzej Lasota on asymptotic stability and recent progress. Opuscula Math. 28(4) (2008), 395–413.Google Scholar
Prato, G. Da and Zabczyk, J.. Ergodicity for Infinite-dimensional Systems (London Mathematical Society Lecture Note Series, 229) . Cambridge University Press, Cambridge, 1996.Google Scholar
Davies, E. B.. Triviality of the peripheral point spectrum. J. Evol. Equ. 5(3) (2005), 407–415.Google Scholar
Ding, Y.. The asymptotic behavior of Frobenius–Perron operator with local lower-bound function. Chaos Solitons Fractals 18(2) (2003), 311–319.Google Scholar
Doob, J. L.. Stochastic Processes. John Wiley–Chapman & Hall, New York–London, 1953.Google Scholar
Eisner, T., Farkas, B., Haase, M. and Nagel, R.. Operator Theoretic Aspects of Ergodic Theory (Graduate Texts in Mathematics, 272) . Springer, Cham, 2015.Google Scholar
Emel’yanov, È. Y.. Conditions for the regularity of Markov semigroups on abstract L 1 -spaces. Mat. Tr. 7(1) (2004), 50–82.Google Scholar
Emel’yanov, É. Y.. Positive asymptotically regular operators in L 1 -spaces and KB-spaces. Positivity IV—Theory and Applications. Technische Universität Dresden, Dresden, 2006, pp. 53–61.Google Scholar
Emel’yanov, E. Y.. Non-spectral Asymptotic Analysis of One-parameter Operator Semigroups (Operator Theory: Advances and Applications, 173) . Birkhäuser, Basel, 2007.Google Scholar
Emel’yanov, E. Y., Kohler, U., Räbiger, F. and Wolff, M. P. H.. Stability and almost periodicity of asymptotically dominated semigroups of positive operators. Proc. Amer. Math. Soc. 129(9) (2001), 2633–2642 (electronic).Google Scholar
Engel, K. and Nagel, R.. One-parameter Semigroups for Linear Evolution Equations (Graduate Texts in Mathematics, 194) . Springer, New York, 2000.Google Scholar
Erkurşun-Özcan, N.. Asymptotic behaviour of operator sequences on KB-spaces. Preprint, 2016,arXiv:org/abs/1403.2114.Google Scholar
Gerlach, M.. On the peripheral point spectrum and the asymptotic behavior of irreducible semigroups of Harris operators. Positivity 17(3) (2013), 875–898.Google Scholar
Gerlach, M.. A Tauberian theorem for strong Feller semigroups. Arch. Math. (Basel) 102(3) (2014), 245–255.Google Scholar
Gerlach, M.. Convergence of dynamics and the Perron–Frobenius operator. Preprint, 2016,arXiv:org/abs/1609.04943.Google Scholar
Gerlach, M. and Kunze, M.. On the lattice structure of kernel operators. Math. Nachr. 288(5–6) (2015), 584–592.Google Scholar
Glück, J.. On the peripheral spectrum of positive operators. Positivity 20(2) (2016), 307–336.Google Scholar
Grobler, J. J.. Spectral theory in Banach lattices. Operator Theory in Function Spaces and Banach Lattices (Operator Theory: Advances and Applications, 75) . Birkhäuser, Basel, 1995, pp. 133–172.Google Scholar
Keicher, V.. On the peripheral spectrum of bounded positive semigroups on atomic Banach lattices. Arch. Math. (Basel) 87(4) (2006), 359–367.Google Scholar
Komorník, J.. Asymptotic periodicity of Markov and related operators. Dynamics Reported: Expositions in Dynamical Systems (N.S.), Vol. 2. Springer, Berlin, 1993, pp. 31–68.Google Scholar
Lasota, A.. Statistical stability of deterministic systems. Equadiff 82 (Würzburg, 1982) (Lecture Notes in Mathematics, 1017) . Springer, Berlin, 1983, pp. 386–419.Google Scholar
Lasota, A. and Mackey, M. C.. Chaos, Fractals, and Noise (Applied Mathematical Sciences, 97) , 2nd edn. Springer, New York, 1994.Google Scholar
Lasota, A. and Rudnicki, R.. Asymptotic behaviour of semigroups of positive operators on C (X). Bull. Pol. Acad. Sci. Math. 36(3–4) (1988), 151–159.Google Scholar
Lasota, A. and Yorke, J. A.. Exact dynamical systems and the Frobenius–Perron operator. Trans. Amer. Math. Soc. 273(1) (1982), 375–384.Google Scholar
Lotz, H. P.. Positive linear operators on L p and the Doeblin condition. Aspects of Positivity in Functional Analysis (Tübingen, 1985) (North-Holland Mathematics Studies, 122) . North-Holland, Amsterdam, 1986, pp. 137–156.Google Scholar
Malczak, J.. An application of Markov operators in differential and integral equations. Rend. Semin. Mat. Univ. Padova 87 (1992), 281–297.Google Scholar
Meyer-Nieberg, P.. Banach Lattices (Universitext) . Springer, Berlin, 1991.Google Scholar
Mischler, S. and Scher, J.. Spectral analysis of semigroups and growth–fragmentation equations. Ann. Inst. H. Poincaré Anal. Non Linéaire 33(3) (2016), 849–898.Google Scholar
Nagel, R.. On the linear operator approach to dynamical systems. Conf. Sem. Mat. Univ. Bari 237–244 (1991), 93–111 ; Proc. Conf. Recent Developments in Mathematical Analysis and its Applications (Bari, Italy, 1990) (in Italian).Google Scholar
Nagel, R. and Räbiger, F.. Superstable operators on Banach spaces. Israel J. Math. 81(1–2) (1993), 213–226.Google Scholar
Pichór, K. and Rudnicki, R.. Continuous Markov semigroups and stability of transport equations. J. Math. Anal. Appl. 249(2) (2000), 668–685.Google Scholar
Pichór, K., Rudnicki, R. and Tyran-Kamińska, M.. Stochastic semigroups and their applications to biological models. Demonstratio Math. 45(2) (2012), 463–494.Google Scholar
Rudnicki, R.. Asymptotic properties of the iterates of positive operators on C (X). Bull. Pol. Acad. Sci. Math. 34(3–4) (1986), 181–187.Google Scholar
Rudnicki, R., Pichór, K. and Tyran-Kamińska, M.. Markov semigroups and their applications. Dynamics of Dissipation. Springer, Berlin–Heidelberg, 2002, pp. 215–238.Google Scholar
Schaefer, H. H.. Banach Lattices and Positive Operators (Die Grundlehren der mathematischen Wissenschaften, 215) . Springer, New York, 1974.Google Scholar
Seneta, E.. Nonnegative Matrices and Markov Chains (Springer Series in Statistics) , 2nd edn. Springer, New York, 1981.Google Scholar
Socała, J.. Asymptotic behaviour of the iterates of nonnegative operators on a Banach lattice. Ann. Polon. Math. 68(1) (1998), 1–16.Google Scholar
Socała, J.. Asymptotic behaviour of the iterates of nonnegative operators on Banach spaces with a cone. Bull. Pol. Acad. Sci. Math. 50(2) (2002), 179–187.Google Scholar
Socała, J.. Asymptotic behaviour of semigroups of nonnegative operators on a Banach lattice. Ann. Polon. Math. 82(2) (2003), 95–103.Google Scholar
Wolff, M. P. H.. Triviality of the peripheral point spectrum of positive semigroups on atomic Banach lattices. Positivity 12(1) (2008), 185–192.Google Scholar
Zalewska-Mitura, A.. A generalization of the lower bound function theorem for Markov operators. Univ. Iagel. Acta Math. 31 (1994), 79–85.Google Scholar