Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T04:29:12.900Z Has data issue: false hasContentIssue false
  • English
  • Français

Local and doubly empirical convergence and the entropy of algebraic actions of sofic groups

Published online by Cambridge University Press:  07 September 2017

BEN HAYES
BEN HAYES*
Affiliation:
Stevenson Center, Nashville, TN 37240, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 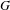$G$ be a sofic group and 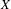$X$ a compact group with 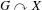$G\curvearrowright X$ by automorphisms. Using (and reformulating) the notion of local and doubly empirical convergence developed by Austin, we show that in many cases the topological and the measure-theoretic entropy with respect to the Haar measure of 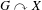$G\curvearrowright X$ agree. Our method of proof recovers all known examples. Moreover, the proofs are direct and do not go through explicitly computing the measure-theoretic or topological entropy.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 4 , April 2019 , pp. 930 - 953
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Austin, T.. Additivity properties of sofic entropy and measures on model spaces. Forum Math. Sigma 4(e25) (2016), 79 pp.Google Scholar
Austin, T.. An asymptotic equipartition property for measures on model spaces. Preprint, 2017,arXiv:1701.08723, Trans. Amer. Math. Soc., to appear.Google Scholar
Berg, K.. Convolution of invariant measures, maximal entropy. Math. Systems Theory 3 (1969), 146–150.Google Scholar
Bowen, L.. Measure conjugacy invariants for actions of countable sofic groups. J. Amer. Math. Soc. 23 (2010), 217–245.Google Scholar
Bowen, L.. Entropy for expansive algebraic actions of residually finite groups. Ergod. Th. & Dynam. Sys. 31(3) (2011), 703–718.Google Scholar
Bowen, L.. Entropy theory for sofic groupoids I: the foundations. J. Anal. Math. 124(1) (2014), 149–233.Google Scholar
Bowen, L. and Li, H.. Harmonic models and spanning forests of residually finite groups. J. Funct. Anal. 263(7) (2012), 1769–1808.Google Scholar
Deninger, C.. Fuglede–Kadison determinants and entropy for actions of discrete amenable groups. J. Amer. Math. Soc. 19 (2006), 737–758.Google Scholar
Gaboriau, D. and Seward, B.. Cost, $\ell ^{2}$ -Betti numbers and the sofic entropy of some algebraic actions. Preprint, 2015, arXiv:1509.02482, J. Anal. Math., to appear.Google Scholar
Hayes, B.. Independence tuples and Deninger’s problem. Groups Geom. Dyn., to appear.Google Scholar
Hayes, B.. Mixing and spectral gap relative to Pinsker factors for sofic groups. Proceedings in Honor of Vaughan F. R. Jones 60th Birthday Conferences, to appear.Google Scholar
Hayes, B.. Polish models and sofic entropy. J. Inst. Math. Jussieu, to appear.Google Scholar
Hayes, B.. Fuglede–Kadison determinants and sofic entropy. Geom. Funct. Anal. 26(2) (2016), 520–606.Google Scholar
Kerr, D.. Sofic measure entropy via finite partitions. Groups Geom. Dyn. 7 (2013), 617–632.Google Scholar
Kerr, D. and Li, H.. Topological entropy and the variational principle for actions of sofic groups. Invent. Math. 186 (2011), 501–558.Google Scholar
Kerr, D. and Li, H.. Soficity, amenability, and dynamical entropy. Amer. J. Math. 135(3) (2013), 721–761.Google Scholar
Kowalski, E.. An Introduction to the Representation Theory of Groups (Graduate Studies in Mathematics, 155) . American Mathematical Society, Providence, RI, 2014.Google Scholar
Li, H.. Sofic mean dimension. Adv. Math. 244 (2014), 570–604.Google Scholar
Li, H. and Liang, B.. Sofic mean length. Preprint, 2015, arXiv:1510.07655.Google Scholar
Li, H., Peterson, J. and Schmidt, K.. Ergodicity of principal algebraic group actions. Recent Trends in Ergodic Theory and Dynamical Systems (Contemporary Mathematics, 631) . American Mathematical Society, Providence, RI, 2015, pp. 201–210.Google Scholar
Lück, W.. L 2 -Invariants: Theory and Applications to Geometry and K-theory. Springer, Berlin, 2002.Google Scholar
Schmidt, K.. Dynamical Systems of Algebraic Origin (Progress in Mathematics, 128) . Birkhäuser, Basel, 1995.Google Scholar