Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-06T04:18:53.627Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear dynamics and recurrence properties defined via essential idempotents of 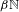$\unicode[STIX]{x1D6FD}\mathbb{N}$

Published online by Cambridge University Press:  13 July 2016

YUNIED PUIG DE DIOS
YUNIED PUIG DE DIOS*
Affiliation:
Università degli Studi di Milano, Dipartimento di Matematica “Federigo Enriques”, Via Saldini 50, 20133 Milano, Italy email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider 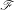$\mathscr{F}$, a non-empty set of subsets of 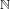$\mathbb{N}$. An operator $T$ on 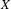$X$ satisfies property 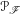${\mathcal{P}}_{\mathscr{F}}$ if, for any non-empty open set 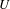$U$ in 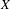$X$, there exists 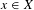$x\in X$ such that 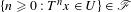$\{n\geq 0:T^{n}x\in U\}\in \mathscr{F}$. Let 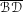$\overline{{\mathcal{B}}{\mathcal{D}}}$ be the collection of sets in 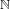$\mathbb{N}$ with positive upper Banach density. Our main result is a characterization of a sequence of operators satisfying property 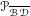${\mathcal{P}}_{\overline{{\mathcal{B}}{\mathcal{D}}}}$, for which we have used a deep result of Bergelson and McCutcheon in the vein of Szemerédi’s theorem. It turns out that operators having property 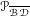${\mathcal{P}}_{\overline{{\mathcal{B}}{\mathcal{D}}}}$ satisfy a kind of recurrence described in terms of essential idempotents of 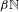$\unicode[STIX]{x1D6FD}\mathbb{N}$. We will also discuss the case of weighted backward shifts. Finally, we obtain a characterization of reiteratively hypercyclic operators.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 1 , February 2018 , pp. 285 - 300
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bayart, F. and Matheron, E.. Dynamics of Linear Operators (Cambridge Tracts in Mathematics, 179) . Cambridge University Press, Cambridge, 2009.CrossRefGoogle Scholar
Bayart, F. and Ruzsa, I.. Difference sets and frequently hypercyclic weighted shifts. Ergod. Th. & Dynam. Sys. 35(3) (2015), 691–709.Google Scholar
Bergelson, V. and Downarowicz, T.. Large sets of integers and hierarchy of mixing properties of measure preserving systems. Colloq. Math. 110(1) (2008), 117–150.CrossRefGoogle Scholar
Bergelson, V. and McCutcheon, R.. Idempotent ultrafilters, multiple weak mixing and Szemerédi’s theorem for generalized polynomials. J. Anal. Math. 111 (2010), 77–130.Google Scholar
Bès, J., Martin, Ö., Peris, A. and Shkarin, S.. Disjoint mixing operators. J. Funct. Anal. 263(5) (2012), 1283–1322.Google Scholar
Bès, J., Menet, Q., Peris, A. and Puig, Y.. Recurrence properties of hypercyclic operators. Math. Ann. (2015), 1–28, doi:10.1007/s00208-015-1336-3.Google Scholar
Bès, J., Menet, Q., Peris, A. and Puig, Y.. Strong transitivity properties for operators. Preprint.Google Scholar
Bès, J. and Peris, A.. Disjointness in hypercyclicity. J. Math. Anal. Appl. 336(1) (2007), 297–315.CrossRefGoogle Scholar
Bonilla, A. and Grosse-Erdmann, K.-G.. Frequently hypercyclic operators and vectors. Ergod. Th. & Dynam. Sys. 27(2) (2007), 383–404.Google Scholar
Bonilla, A. and Grosse-Erdmann, K.-G.. Erratum: Frequently hypercyclic operators and vectors. Ergod. Th. & Dynam. Sys. 29(6) (2009), 1993–1994.Google Scholar
Costakis, G. and Parissis, I.. Szemerédi’s theorem, frequent hypercyclicity and multiple recurrence. Math. Scand. 110(2) (2012), 251–272.Google Scholar
Furstenberg, H.. Ergodic behaviour of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.Google Scholar
Grosse-Erdmann, K.-G. and Peris, A.. Linear Chaos (Universitext) . Springer, London, 2011.Google Scholar
Hindman, N. and Strauss, D.. Algebra in the Stone–Čech Compactification. Theory and Applications (Expositions in Mathematics, 27) . De Gruyter, Berlin, 1998.Google Scholar
Hindman, N. and Strauss, D.. Density in arbitrary semigroups. Semigroup Forum 73(2) (2006), 273–300.Google Scholar
Menet, Q.. Linear chaos and frequent hypercyclicity. Trans. Amer. Math. Soc., to appear. doi:10.1090/tran/6808.Google Scholar
Stewart, C. L. and Tijdeman, R.. On infinite-difference sets. Canad. J. Math. 31(5) (1979), 897–910.CrossRefGoogle Scholar