Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T17:58:26.821Z Has data issue: false hasContentIssue false
  • English
  • Français

Limit drift for complex Feigenbaum mappings

Part of: Complex dynamical systems

Published online by Cambridge University Press:  28 September 2020

GENADI LEVIN  and
GRZEGORZ ŚWIA̧TEK
GENADI LEVIN
Affiliation:
Einstein Institute of Mathematics, Hebrew University, Givat Ram91904, Jerusalem, Israel (e-mail: [email protected])
GRZEGORZ ŚWIA̧TEK
Affiliation:
Department of Mathematics and Information Science, Politechnika Warszawska, Koszykowa 75, 00-662, Warszawa, Poland (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the dynamics of towers defined by fixed points of renormalization for Feigenbaum polynomials in the complex plane with varying order 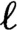$\ell $ of the critical point. It is known that the measure of the Julia set of the Feigenbaum polynomial is positive if and only if almost every point tends to 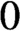$0$ under the dynamics of the tower for corresponding 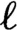$\ell $ . That in turn depends on the sign of a quantity called the drift. We prove the existence and key properties of absolutely continuous invariant measures for tower dynamics as well as their convergence when 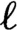$\ell $ tends to 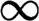$\infty $ . We also prove the convergence of the drifts to a finite limit, which can be expressed purely in terms of the limiting tower, which corresponds to a Feigenbaum map with a flat critical point.

Keywords

Feigenbaum functionmeasure of Julia setinvariant measurelimit drift

MSC classification

Primary: 37F25: Renormalization
Secondary: 37F35: Conformal densities and Hausdorff dimension
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 8 , August 2021 , pp. 2428 - 2479
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bochner, S. and Martin, W.. Several Complex Variables. Princeton University Press, Princeton, NJ, 1948.Google Scholar
Bruin, H., Keller, G., Nowicki, T. and Van Strien, S.. Wild Cantor attractors exist. Ann. Math. 143 (1996), 97–130.CrossRefGoogle Scholar
Coullet, P. and Tresser, C.. Iteration d’endomorphismes et groupe de renormalisation. C. R. Acad. Sci. 287 A (1978),5.Google Scholar
Dudko, A. and Sutherland, S.. On the Lebesgue measure of the Feigenbaum Julia set. Invent. Math. 221 (2020), 167–202.CrossRefGoogle Scholar
Eckmann, J.-P. and Wittwer, P.. Computer Methods and Borel Summability Applied to Feigenbaum’s Equation (Lecture Notes in Physics, 277). Springer, Berlin, 1985.CrossRefGoogle Scholar
Epstein, H. and Lascoux, J.. Analyticity properties of the Feigenbaum function. Comm. Math. Phys. 81 (1981), 437–453.CrossRefGoogle Scholar
Feigenbaum, M.. Qualitative universality for a class of non-linear transformations. J. Stat. Phys. 19 (1978), 25–52.CrossRefGoogle Scholar
Feigenbaum, M.. The universal metric properties of non-linear transformations. J. Stat. Phys. 21 (1979), 669–706.CrossRefGoogle Scholar
Lehto, O. and Virtanen, K.. Quasiconformal Mappings in the Plane, 2nd edn. Springer, Berlin, 1973.CrossRefGoogle Scholar
Levin, G. and Świa̧tek, G.. Dynamics and universality of unimodal mappings with infinite criticality. Comm. Math. Phys. 258 (2005), 103–133.CrossRefGoogle Scholar
Levin, G. and Świa̧tek, G.. Hausdorff dimension of Julia sets of Feigenbaum polynomials with high criticality. Comm. Math. Phys. 258 (2005), 135–148.CrossRefGoogle Scholar
Levin, G. and Świa̧tek, G.. Common limits of Fibonacci circle maps. Comm. Math. Phys. 312 (2012), 695–734.CrossRefGoogle Scholar
Levin, G. and Świa̧tek, G.. Measure of the Julia set of the Feigenbaum map with infinite criticality. Ergod. Th. & Dynam. Sys. 30 (2010), 855–875.CrossRefGoogle Scholar
Levin, G. and Świa̧tek, G.. Limit drift. Ergod. Th. & Dynam. Sys. 37(8) (2017), 2643–2670.CrossRefGoogle Scholar
Mc Mullen, C.. Renormalization and 3-manifolds which Fiber over the Circle (Annals of Mathematics Studies, 142). Princeton University Press, Princeton, NJ, 1998.Google Scholar
McMullen, C.. Hausdorff dimension and conformal dynamics II: Geometrically finite rational maps. Comment. Math. Helv. 75 (2000), 535–593.CrossRefGoogle Scholar
Van Strien, S. and Nowicki, T.. Polynomial maps with a Julia set of positive Lebesgue measure: Fibonacci maps. Preprint, 1994, arXiv:math/9402215.Google Scholar