Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T03:53:14.379Z Has data issue: false hasContentIssue false
  • English
  • Français

Lebesgue measure of escaping sets of entire functions

Published online by Cambridge University Press:  11 May 2018

WEIWEI CUI
WEIWEI CUI*
Affiliation:
Mathematisches Seminar, Christian-Albrechts-Universität zu Kiel, Ludewig-Meyn-Str. 4, 24098 Kiel, Germany email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a transcendental entire function 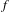$f$ of finite order in the Eremenko–Lyubich class 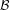${\mathcal{B}}$, we give conditions under which the Lebesgue measure of the escaping set 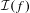${\mathcal{I}}(f)$ of 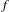$f$ is zero. This complements the recent work of Aspenberg and Bergweiler [Math. Ann. 352(1) (2012), 27–54], in which they give conditions on entire functions in the same class with escaping sets of positive Lebesgue measure. We will construct an entire function in the Eremenko–Lyubich class to show that the condition given by Aspenberg and Bergweiler is essentially sharp. Furthermore, we adapt our idea of proof to certain infinite-order entire functions. Under some restrictions to the growth of these entire functions, we show that the escaping sets have zero Lebesgue measure. This generalizes a result of Eremenko and Lyubich.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 1 , January 2020 , pp. 89 - 116
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aspenberg, M. and Bergweiler, W.. Entire functions with Julia sets of positive measure. Math. Ann. 352(1) (2012), 27–54.10.1007/s00208-010-0625-0Google Scholar
Ahlfors, L. V.. Lectures on Quasiconformal Mappings (University Lecture Series, 38) , 2nd edn. American Mathematical Society, Providence, RI, 2006.Google Scholar
Bergweiler, W. and Chyzhykov, I.. Lebesgue measure of escaping sets of entire functions of completely regular growth. J. Lond. Math. Soc. (2) 94(2) (2016), 639–661.Google Scholar
Bergweiler, W.. Iteration of meromorphic functions. Bull. Amer. Math. Soc. (N.S.) 29(2) (1993), 151–188.Google Scholar
Bergweiler, W., Fagella, N. and Rempe-Gillen, L.. Hyperbolic entire functions with bounded Fatou components. Comment. Math. Helv. 90(4) (2015), 799–829.10.4171/CMH/371Google Scholar
Bergweiler, W., Rippon, P. J. and Stallard, G. M.. Dynamics of meromorphic functions with direct or logarithmic singularities. Proc. Lond. Math. Soc. (3) 97(2) (2008), 368–400.Google Scholar
Eremenko, A. and Lyubich, M.. Dynamical properties of some classes of entire functions. Ann. Inst. Fourier (Grenoble) 42(4) (1992), 989–1020.10.5802/aif.1318Google Scholar
Eremenko, A.. On the iteration of entire functions. Dynamical Systems and Ergodic Theory (Warsaw, 1986) (Banach Center Publications, 23) . PWN, Warsaw, 1989, pp. 339–345.Google Scholar
Falconer, K. J.. Fractal Geometry: Mathematical Foundations and Applications, 2nd edn. John Wiley & Sons, Inc., Hoboken, NJ, 2003.Google Scholar
Fatou, P.. Sur l’itération des fonctions transcendantes entières. Acta Math. 47(4) (1926), 337–370.Google Scholar
Goldberg, A. A. and Ostrovskii, I. V.. Value Distribution of Meromorphic Functions (Translations of Mathematical Monographs, 236) . American Mathematical Society, Providence, RI, 2008.Google Scholar
Hayman, W. K.. Meromorphic Functions (Oxford Mathematical Monographs) . Clarendon Press, Oxford, 1964.Google Scholar
McMullen, C. T.. Area and Hausdorff dimension of Julia sets of entire functions. Trans. Amer. Math. Soc. 300(1) (1987), 329–342.10.1090/S0002-9947-1987-0871679-3Google Scholar
Milnor, J.. Dynamics in One Complex Variable (Annals of Mathematics Studies, 160) . Princeton University Press, Princeton, NJ, 2006.Google Scholar
Misiurewicz, M.. On iterates of e z . Ergod. Th. & Dynam. Sys. 1(1) (1981), 103–106.10.1017/S014338570000119XGoogle Scholar
Nevanlinna, R.. Analytic Functions (Grundlehren der mathematischen Wissenschaften, 162) . Springer, New York–Berlin, 1970, translated from the second German edition by Phillip Emig.Google Scholar
Pommerenke, Ch.. Boundary Behaviour of Conformal Maps (Grundlehren der mathematischen Wissenschaften, 299) . Springer, Berlin, 1992.Google Scholar
Rempe, L.. Rigidity of escaping dynamics for transcendental entire functions. Acta Math. 203(2) (2009), 235–267.10.1007/s11511-009-0042-yGoogle Scholar
Rempe-Gillen, L.. Arc-like continua, Julia sets of entire functions, and Eremenko’s Conjecture. Preprint, 2016, arXiv:1610.06278.Google Scholar
Rempe-Gillen, L. and Sixsmith, D. J.. Hyperbolic entire functions and the Eremenko–Lyubich class: Class 𝓑 or not class 𝓑? Math. Z. 286(3–4) (2017), 783–800.10.1007/s00209-016-1784-9Google Scholar
Rottenfusser, G., Rückert, J., Rempe, L. and Schleicher, D.. Dynamic rays of bounded-type entire functions. Ann. of Math. (2) 173(1) (2011), 77–125.Google Scholar
Schleicher, D.. Dynamics of entire functions. Holomorphic Dynamical Systems (Lecture Notes in Mathematics, 1998) . Springer, Berlin, 2010, pp. 295–339.Google Scholar
Tsuji, M.. Potential Theory in Modern Function Theory. Chelsea Publishing, New York, 1975.Google Scholar