Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-27T20:15:18.142Z Has data issue: false hasContentIssue false
  • English
  • Français

The lap-counting function for linear mod one transformations I: explicit formulas and renormalizability

Published online by Cambridge University Press:  19 September 2008

Leopold Flatto  and
Jeffrey C. Lagarias
Leopold Flatto
Affiliation:
AT&T Bell Laboratories, Murray Hill, New Jersey 07974, USA
Jeffrey C. Lagarias
Affiliation:
AT&T Bell Laboratories, Murray Hill, New Jersey 07974, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Linear mod one transformations are the maps of the unit interval given by fβα(x) = βx + α (mod 1), with β > 1 and 0 ≤ α < 1. The lap-counting function is the function 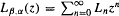where the lap number Ln essentially counts the number of monotonic pieces of the nth iterate 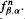. We derive an explicit factorization formula for Lβα(z) which directly shows that Lβα(z) is a function meromorphic in the open unit disk {z: |z| < 1} and analytic in the open disk {z: |z| < 1/β}, with a simple pole at z = 1/β.Comparison with a known formula for the Artin—Mazur—Ruelle zeta function ζβ,α(z) of fβα shows that Lβα(z) and ζβ,α(z) have identical sets of singularities in the disk {z: |z| < 1}. We derive two more factorization formulae for Lβ,α(z) valid for certain parameter ranges of (β, α). When 1 < α + β ≤ 2, there is sometimes a ‘renormalization’ structure of such maps present, which has previously been studied in connection with simplified models for the Lorenz attractor. In the case that fβα is non-trivially renormalizable, we obtain a factorization formula for Lβα(z). For (β, α) in a region 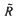contained in 2 < α + β ≤ 3 we obtain a factorization formula which relates Lβα(z) to a ‘rescaled’ lap-counting function from the region 1 < α + β ≤ 2. The various factorizations exhibit certain singularities of Lβα(z) on the circle |z| = 1/β. These singularities are related to topological dynamical properties of fβ,α. In parts II and III we show that these comprise the complete set of such singularities on the circle |z| = 1/β.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 16 , Issue 3 , June 1996 , pp. 451 - 491
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Artin, M. and Mazur, B.. On periodic points. Ann. Math. 81 (1965), 82–99.CrossRefGoogle Scholar
[2]Baladi, V. and Ruelle, D.. An extension of the theorem of Milnor and Thurston on the zeta functions of interval maps. Ergod. Th. & Dynam. Sys. 14 (1994), 621–632.CrossRefGoogle Scholar
[3]Carlson, F.. Über Potenzreihen mit ganzzahlingen Koeffizienten. Math. Z. 9 (1921), 1–13.CrossRefGoogle Scholar
[4]Denker, M., Grillenberger, C. and Sigmund, K.. Ergodk theory on compact spaces (Lecture Notes in Math. 527). Springer, Berlin, 1976.CrossRefGoogle Scholar
[5]Flatto, L.. Z-Numbers and β-transformations. Symbolic Dynamics and Its Applications (Contemporary Math. 135). Ed. Walters, P.. AMS, Providence, RI, 1992, pp. 181–202.CrossRefGoogle Scholar
[6]Flatto, L. and Lagarias, J. C.. The lap-counting function of the linear mod one transformation II. Markov chain for generalized lap numbers. Ergod. Th. & Dynam. Sys. To appear.Google Scholar
[7]Flatto, L. and Lagarias, J. C.. The lap-counting function of the linear mod one transformation III. Period of Markov chain. Ergod. Th. & Dynam. Sys. To appear.Google Scholar
[8]Flatto, L., Lagarias, J. C. and Pollington, A.. On the range of values . Acta Arithmetica 70 (1995), 125–147.CrossRefGoogle Scholar
[9]Flatto, L., Lagarias, J. C. and Poonen, B.. The zeta function of the beta transformation. Ergod. Th. & Dynam. Sys. 14 (1994), 237–266.CrossRefGoogle Scholar
[10]Frougny, C. and Solomyak, B.. Finite β-expansions. Ergod. Th. & Dynam. Sys. 12 (1992), 713–723.CrossRefGoogle Scholar
[11]Glendinning, P.. Topological conjugation of Lorenz maps by β-transformations. Math. Proc. Camb. Phil. Soc. 107 (1990), 401–413.CrossRefGoogle Scholar
[12]Glendinning, P. and Sparrow, C. T.. Prime and renormalizable kneading invariants and the dynamics of expanding Lorenz maps. Physica D 62 (1993), 22–50.Google Scholar
[13]Halfin, S.. Explicit construction of invariant measures for a class of continuous state Markov processes. Ann. Prob. 3 (1975), 859–864.CrossRefGoogle Scholar
[14]Hofbauer, F.. On intrinsic ergodicity of piecewise monotonic transformations with positive entropy. Israel J. Math. 34 (1979), 213–237.CrossRefGoogle Scholar
[15]Hofbauer, F.. l measures for piecewise monotonic functions on [0, 1]. Ergodic Theory (Lecture Notesin Math. 729). Ed. Denker, M.. Springer, Berlin, 1979, pp. 66–77.CrossRefGoogle Scholar
[16]Hofbauer, F.. Maximal measures for simple piecewise monotonic transformations. Z Warsch. Geb. 52 (1980), 289–300.CrossRefGoogle Scholar
[17]Hofbauer, F.. The maximal measure for linear mod one transformations. J. London Math. Soc. 23 (1981), 92–112.CrossRefGoogle Scholar
[18]Hofbauer, F.. The structure of piecewise monotonic transformations. Ergod. Th. & Dynam. Sys. 1 (1981), 159–178.CrossRefGoogle Scholar
[19]Hofbauer, F.. Hausdorff dimension and pressure for piecewise monotonic maps of the interval. J. London Math. Soc. 47 (1993), 142–156.CrossRefGoogle Scholar
[20]Hofbauer, F. and Keller, G.. Zeta-functions and transfer-operators for piecewise linear transformations. J. reine Angew. 352 (1984), 100–113.Google Scholar
[21]Hubbard, J. T. and Sparrow, C. T.. The classification of topologically expansive Lorenz maps. Comm. Pure Appl. Math. 43 (1990), 431–443.CrossRefGoogle Scholar
[22]Ito, S. and Takahashi, Y.. Markov subshifts and realization of β-expansions. J. Math. Soc. Japan 26 (1974), 33–55.Google Scholar
[23]Milnor, J. and Thurston, W.. On iterated maps of the interval. Lecture Notes in Math. 1342. Springer, Berlin, 1988, pp 465–563.Google Scholar
[24]Mori, M.. Fredholm determinant for piecewise linear transformations. Osaka J. Math. 27 (1990), 81–116.Google Scholar
[25]Palmer, M. R.. On the classification of measure preserving transformations of Lebesgue spaces. Ph.D. Thesis. University of Warwick, 1979.Google Scholar
[26]Parry, W.. On the β-expansions of real numbers. Acta Math. Acad. Sci. Hung. 11 (1960), 401–416.CrossRefGoogle Scholar
[27]Parry, W.. Representations for real numbers. Acta Math. Acad. Sci. Hung. 15 (1964), 95–105.CrossRefGoogle Scholar
[28]Parry, W.. Symbolic dynamics and transformations of the unit interval. Trans. Amer. Math. Soc. 122 (1966), 368–378.CrossRefGoogle Scholar
[29]Parry, W.. The Lorenz attractor and a related population model. Ergodic Theory (Lecture Notes in Math. 729). Eds. Denker, M. and Jacobs, K.. Springer, Berlin, 1979, pp. 169–187.Google Scholar
[30]Polya, G.. Sur les séries entières a coefficients entiers. Proc. London Math. Soc. 21 (1923), 22–38.CrossRefGoogle Scholar
[31]Preston, C.. Iterates of Piecewise Monotone Mappings on an Interval (Lecture Notes in Math. 1347). Springer, New York, 1988.CrossRefGoogle Scholar
[32]Preston, C.. What you need to know to knead. Adv. in Math. 78 (1989), 192–252.CrossRefGoogle Scholar
[33]Rand, D. M.. The topological classification of Lorenz attractors. Math. Proc. Camb. Phil. Soc. 83 (1978), 451–460.CrossRefGoogle Scholar
[34]Renyi, A.. Representations for real numbers and their ergodic properties. Acta Math. Acad. Sci. Hung. 8 (1957), 477–493.CrossRefGoogle Scholar
[35]Ruelle, D.. Dynamical Zeta Functions for Piecewise Monotone Maps of the Interval. (CRM Monographs vol. 4). AMS, 1994.Google Scholar
[36]Solomyak, V.. Conjugates of beta-numbers and a zero-free domain for a class of analytic functions. Proc. London Math. Soc. 68 (1994), 477–498.CrossRefGoogle Scholar
[37]Sparrow, C. T.. The Lorenz Equations: Bifurcations, Chaos and Strange Attractors (Applied Math Sciences, vol. 41). Springer, New York, 1982.CrossRefGoogle Scholar
[38]Swinnerton-Dyer, H. P. F.. The basic Lorenz list and Sparrow's conjecture A. J. London Math. Soc. 29 (1984), 509–520.CrossRefGoogle Scholar
[39]Takahashi, Y.. β-transformations and symbolic dynamics. Proc. Second Japan—USSR Symposium on Probability Theory (Lecture Notes in Math. 330). Springer, New York, 1973, pp. 455–464.CrossRefGoogle Scholar
[40]Takahashi, Y.. Shift with orbit basis and realization of one-dimensional maps. Osaka Math. J. 20 (1983), 599–629 (Correction: 21 (1985), 637).Google Scholar
[41]Wilkinson, K. M.. Ergodic properties of certain linear mod one transformations. Adv. in Math. 14 (1974), 64–72.CrossRefGoogle Scholar
[42]Wilkinson, K. M.. Ergodic properties of a class of piecewise linear transformations. Z. Warsch. Geb. 31 (1975), 303–328.CrossRefGoogle Scholar
[43]Williams, R. F.. The structure of Lorenz attractors. lnst. Hautes Etudes Sci. Publ. Math. 50 (1979), 321–347.Google Scholar