Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T03:59:40.314Z Has data issue: false hasContentIssue false
  • English
  • Français

Julia sets converging to filled quadratic Julia sets

Published online by Cambridge University Press:  21 August 2012

ROBERT T. KOZMA  and
ROBERT L. DEVANEY
ROBERT T. KOZMA
Affiliation:
Department of Mathematics, Boston University, 111 Cummington Street, Boston, MA 02215, USA (email: [email protected])
ROBERT L. DEVANEY
Affiliation:
Department of Mathematics, Boston University, 111 Cummington Street, Boston, MA 02215, USA (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we consider singular perturbations of the quadratic polynomial 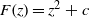$F(z) = z^2 + c$ where $c$ is the center of a hyperbolic component of the Mandelbrot set, i.e., rational maps of the form 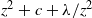$z^2 + c + \lambda /z^2$. We show that, as 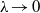$\lambda \rightarrow 0$, the Julia sets of these maps converge in the Hausdorff topology to the filled Julia set of the quadratic map 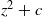$z^2 + c$. When $c$ lies in a hyperbolic component of the Mandelbrot set but not at its center, the situation is much simpler and the Julia sets do not converge to the filled Julia set of 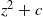$z^2 + c$.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 34 , Issue 1 , February 2014 , pp. 171 - 184
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Blanchard, P., Devaney, R. L., Look, D. M., Seal, P. and Shapiro, Y.. Sierpinski curve Julia sets and singular perturbations of complex polynomials. Ergod. Th. & Dynam. Sys. 25 (2005), 1047–1055.Google Scholar
[2]Blanchard, P., Devaney, R. L., Garijo, A. and Russell, E. D.. A generalized version of the McMullen domain. Internat. J. Bifur. Chaos 18 (2008), 2309–2318.Google Scholar
[3]Ble, G., Douady, A. and Henriksen, C.. Round annuli. In the Tradition of Ahlfors and Bers, III (Contemporary Mathematics, 355). American Mathematical Society, Providence, RI, 2004, pp. 71–76.Google Scholar
[4]Devaney, R. L.. Cantor necklaces and structurally unstable Sierpinski curve Julia sets for rational maps. Qual. Theory Dyn. Syst. 5 (2006), 337–359.Google Scholar
[5]Devaney, R. L.. Cantor sets of circles of Sierpinski curve Julia sets. Ergod. Th. & Dynam. Sys. 27 (2007), 1525–1539.Google Scholar
[6]Devaney, R. L. and Garijo, A.. Julia sets converging to the unit disk. Proc. Amer. Math. Soc. 136 (2008), 981–988.Google Scholar
[7]Devaney, R. L., Look, D. M. and Uminsky, D.. The escape trichotomy for singularly perturbed rational maps. Indiana Univ. Math. J. 54 (2005), 1621–1634.Google Scholar
[8]Devaney, R. L. and Morabito, M.. Limiting Julia sets for singularly perturbed rational maps. Internat. J. Bifur. Chaos 18 (2008), 3175–3181.Google Scholar
[9]Garijo, A., Marotta, S. and Russell, E.. Singular perturbations in the quadratic family with multiple poles. J. Difference Equ. Appl. to appear.Google Scholar
[10]Marotta, S.. Singular perturbations in the quadratic family. J. Difference Equ. Appl. 4 (2008), 581–595.Google Scholar
[11]McMullen, C.. Automorphisms of rational maps. Holomorphic Functions and Moduli I (Mathematical Sciences Research Institute Publications, 10). Springer, New York, 1988.Google Scholar
[12]Milnor, J.. Dynamics in One Complex Variable. Vieweg, Wiesbaden, 1999.Google Scholar