Joint spectral radius, Sturmian measures and the finiteness conjecture

Abstract

The joint spectral radius of a pair of 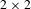$2\times 2$ real matrices 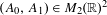$(A_{0},A_{1})\in M_{2}(\mathbb{R})^{2}$ is defined to be 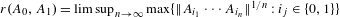$r(A_{0},A_{1})=\limsup _{n\rightarrow \infty }\max \{\Vert A_{i_{1}}\cdots A_{i_{n}}\Vert ^{1/n}:i_{j}\in \{0,1\}\}$, the optimal growth rate of the norm of products of these matrices. The Lagarias–Wang finiteness conjecture [Lagarias and Wang. The finiteness conjecture for the generalized spectral radius of a set of matrices. Linear Algebra Appl.214 (1995), 17–42], asserting that 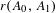$r(A_{0},A_{1})$ is always the $n$th root of the spectral radius of some length-$n$ product 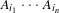$A_{i_{1}}\cdots A_{i_{n}}$, has been refuted by Bousch and Mairesse [Asymptotic height optimization for topical IFS, Tetris heaps, and the finiteness conjecture. J. Amer. Math. Soc.15 (2002), 77–111], with subsequent counterexamples presented by Blondel et al [An elementary counterexample to the finiteness conjecture. SIAM J. Matrix Anal.24 (2003), 963–970], Kozyakin [A dynamical systems construction of a counterexample to the finiteness conjecture. Proceedings of the 44th IEEE Conference on Decision and Control, and the European Control Conference (Seville, Spain, December 2005). IEEE, Piscataway, NJ, pp. 2338–2343] and Hare et al [An explicit counterexample to the Lagarias–Wang finiteness conjecture. Adv. Math.226 (2011), 4667–4701]. In this article, we introduce a new approach to generating finiteness counterexamples, and use this to exhibit an open subset of 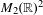$M_{2}(\mathbb{R})^{2}$ with the property that each member 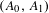$(A_{0},A_{1})$ of the subset generates uncountably many counterexamples of the form 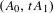$(A_{0},tA_{1})$. Our methods employ ergodic theory; in particular, the analysis of Sturmian invariant measures. This approach allows a short proof that the relationship between the parameter $t$ and the Sturmian parameter 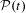${\mathcal{P}}(t)$ is a devil’s staircase.