Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T12:22:06.048Z Has data issue: false hasContentIssue false
  • English
  • Français

Joint ergodicity for group actions

Published online by Cambridge University Press:  19 September 2008

Vitaly Bergelson  and
Joseph Rosenblatt
Vitaly Bergelson
Affiliation:
The Ohio State University, Columbus, Ohio 43210, USA
Joseph Rosenblatt
Affiliation:
The Ohio State University, Columbus, Ohio 43210, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T1,…,Tn be continuous representations of a σ-compact separable locally compact amenable group G as measure-preserving transformations of a non-atomic separable probability space (X, β, m). Let (Kn) be a right Følner sequence of compact sets in G. If T1,…,Tn are pairwise commuting in the sense that Ti(g)Tj(h) = Tj(h)Ti(g) for i ≠ j and g, h ∈ G, then necessary and sufficient conditions can be given, in terms of the ergodicity of certain tensor products, for the following to hold: for all F1,…,Fn∈L∞, the sequence AN(x) where

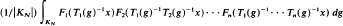
converges in L2(X) to 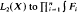. The necessary and sufficient conditions are that each of the following representations are ergodic: Tn, Tn−1⊗Tn−1Tn,…,T2⊗T2T3⊗…⊗T2…Tn, T1⊗T1T2⊗…⊗T1…Tn.

In order to prove this theorem, specific properties of the decomposition of L2(X) into its weakly mixing and compact subspaces with respect to a representation Ti are needed. These properties are also used to prove some generalizations of wellknown facts from ergodic theory in the case where G is the integer group Z.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 8 , Issue 3 , September 1988 , pp. 351 - 364
Copyright
Copyright © Cambridge University Press 1988

References

REFERENCES

[1]Berend, D. & Bergelson, V.. Jointly ergodic measure preserving transformations. Israel J. Math. 49 (1984), 307–314.CrossRefGoogle Scholar
[2]Berend, D. & Bergelson, V.. Characterization of joint ergodicity for non-commuting transformations. Israel J. Math. 56 (1986), 123–8.CrossRefGoogle Scholar
[3]Bergelson, V. & Rosenblatt, J.. Mixing actions of groups, to appear in Illinois J. Math.Google Scholar
[4]Deleeuw, K. & Glicksberg, I.. Applications of almost periodic compactifications. Acta Math. 105 (1961), 63–97.CrossRefGoogle Scholar
[5]Dunford, N. & Schwartz, J.. Linear Operators Vol. I. Interscience, New York, 1964.Google Scholar
[6]Dye, H.. On the ergodic mixing theorem. TAMS 118 (1965), 123–130.CrossRefGoogle Scholar
[7]Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemeredi on arithmetic progressions. J. d'Analyse Math. 31 (1977), 204–256.CrossRefGoogle Scholar
[8]Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory Princeton University Press, Princeton, New Jersey, 1981.CrossRefGoogle Scholar
[9]Furstenberg, H. & Katznelson, Y.. An ergodic Szemeredi theorem for commuting transformations. J. d'Analyse 34 (1978), 275–291.CrossRefGoogle Scholar
[10]Furstenberg, H., Katznelson, Y. & Ornstein, D.. The ergodic theoretical proof of Szemeredi's theorem. BAMS 7 (1982), 527–552.CrossRefGoogle Scholar
[11]Greenleaf, F. & Moskowitz, M.. Cyclic vectors for representations of locally compact groups. Math. Annalen 190 (1971), 265–288.CrossRefGoogle Scholar
[12]Halmos, P.. Lectures in Ergodic Theory. Math. Soc. of Japan, Kenkyusha, Tokyo, 1956.Google Scholar
[13]Hewitt, E. & Ross, K.. Abstract Harmonic Analysis Vol. II, Springer-Verlag, New York, Heidelberg, Berlin, 1970.Google Scholar
[14]Krengel, V.. Ergodic Theorems Walter de Cruyter, Berlin, New York, 1985.CrossRefGoogle Scholar
[15]Loomis, L.. An Introduction to Abstract Harmonic Analysis Van Nostrand, Toronto, New York, London, 1953.Google Scholar
[16]Mackey, G.. Ergodic transformation groups with a pure point spectrum. Ill. J. Math. 8 (1964), 593–600.Google Scholar
[17]Moore, C. C.. Ergodicity of flows on homogeneous spaces. Amer. J. Math. 88 (1960), 154–178.CrossRefGoogle Scholar
[18]Neveu, J.. Processes Aléatoires Gaussiens Presses V. of Montreal, Montreal, 1968.Google Scholar
[19]Schmidt, K.. Asymptotic properties of unitary representations and mixing. Proc. London Math. 48 (1984), 445–460.CrossRefGoogle Scholar
[20]Zimmer, R.. Extensions of ergodic group actions. Ill. J. Math. 20 (1976), 373–409.Google Scholar