Article contents
 ${\it\alpha}$-Hölder linearization of hyperbolic diffeomorphisms with resonance
${\it\alpha}$-Hölder linearization of hyperbolic diffeomorphisms with resonance
Published online by Cambridge University Press: 11 August 2014
Abstract
Concerning hyperbolic diffeomorphisms, one expects a better smoothness of linearization, but it may be confined by resonance among eigenvalues. Hartman gave a three-dimensional analytic mapping with resonance which cannot be linearized by a Lipschitz conjugacy. Since then, efforts have been made to give the  ${\it\alpha}$-Hölder continuity of the conjugacy and hope the exponent
${\it\alpha}$-Hölder continuity of the conjugacy and hope the exponent  ${\it\alpha}<1$ can be as large as possible. Recently, it was proved for some weakly resonant hyperbolic diffeomorphisms that
${\it\alpha}<1$ can be as large as possible. Recently, it was proved for some weakly resonant hyperbolic diffeomorphisms that  ${\it\alpha}$ can be as large as we expect. In this paper we prove that this result holds for all
${\it\alpha}$ can be as large as we expect. In this paper we prove that this result holds for all 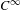 $C^{\infty }$ weakly resonant hyperbolic diffeomorphisms.
$C^{\infty }$ weakly resonant hyperbolic diffeomorphisms.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2014
References
- 5
- Cited by


