No CrossRef data available.
Article contents
Invariant random subgroups of semidirect products
Published online by Cambridge University Press: 04 September 2018
Abstract
We study invariant random subgroups (IRSs) of semidirect products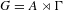 
$G=A\rtimes \unicode[STIX]{x1D6E4}$. In particular, we characterize all IRSs of parabolic subgroups of 
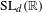$\text{SL}_{d}(\mathbb{R})$, and show that all ergodic IRSs of 
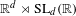$\mathbb{R}^{d}\rtimes \text{SL}_{d}(\mathbb{R})$ are either of the form 
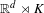$\mathbb{R}^{d}\rtimes K$ for some IRS of 
$\text{SL}_{d}(\mathbb{R})$, or are induced from IRSs of 
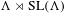$\unicode[STIX]{x1D6EC}\rtimes \text{SL}(\unicode[STIX]{x1D6EC})$, where 
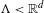$\unicode[STIX]{x1D6EC}<\mathbb{R}^{d}$ is a lattice.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2018
References
Abért, M., Bergeron, N., Biringer, I., Gelander, T., Nikolov, N., Raimbault, J. and Samet, I.. On the growth of L
2 -invariants for sequences of lattices in Lie groups. Ann. of Math. (2)
185(3) (2017), 711–790.Google Scholar
Abért, M., Glasner, Y. and Virág, B.. Kesten’s theorem for invariant random subgroups. Duke Math. J.
163(3) (2014), 465–488.Google Scholar
Bader, U., Duchesne, B., Lécureux, J. and Wesolek, P.. Amenable invariant random subgroups. Israel J. Math.
1 (2014), 1–24.Google Scholar
Bekka, B.. Operator-algebraic superridigity for sl n (z), n ≥ 3. Invent. Math.
169(2) (2007), 401–425.Google Scholar
Benedetti, R. and Petronio, C.. Lectures on Hyperbolic Geometry
(Universitext)
. Springer, Berlin, 1992.Google Scholar
Biringer, I. and Tamuz, O.. Unimodularity of invariant random subgroups. Trans. Amer. Math. Soc.
369(6) (2017), 4043–4061.Google Scholar
Bowen, L.. Random walks on random coset spaces with applications to Furstenberg entropy. Invent. Math.
196(2) (2014), 485–510.Google Scholar
Bowen, L.. Invariant random subgroups of the free group. Groups Geom. Dyn.
9(3) (2015), 891–916.Google Scholar
Bowen, L., Grigorchuk, R. and Kravchenko, R.. Invariant random subgroups of lamplighter groups. Israel J. Math.
207(2) (2015), 763–782.Google Scholar
Chabauty, C.. Limite d’ensembles et géométrie des nombres. Bull. Soc. Math. France
78 (1950), 143–151.Google Scholar
Diatta, A. and Foreman, B.. Lattices in contact Lie groups and 5-dimensional contact solvmanifolds. Kodai Math. J.
38(1) (2015), 228–248.Google Scholar
Furstenberg, H.. A note on Borel’s density theorem. Proc. Amer. Math. Soc.
55(1) (1976), 209–212.Google Scholar
Hartman, Y. and Tamuz, O.. Furstenberg entropy realizations for virtually free groups and lamplighter groups. J. Anal. Math.
126(1) (2015), 227–257.Google Scholar
Knapp, A. W.. Lie Groups Beyond an Introduction. Springer Science & Business Media, Switzerland, 2013, p. 140.Google Scholar
Nevo, A. and Zimmer, R. J.. A generalization of the intermediate factors theorem. J. Anal. Math.
86(1) (2002), 93–104.Google Scholar
Phelps, R. R.. Lectures on Choquet’s Theorem
(Lecture Notes in Mathematics, 1757)
, 2nd edn. Springer, Berlin, 2001.Google Scholar
Raghunathan, M. S.. Discrete Subgroups of Lie Groups
(Ergebnisse der Mathematik und ihrer Grenzgebiete, 68)
. Springer, New York, 1972.Google Scholar
Stuck, G. and Zimmer, R. J.. Stabilizers for ergodic actions of higher rank semisimple groups. Ann. of Math. (2)
3 (1994), 723–747.Google Scholar
Thomas, S. and Tucker-Drob, R.. Invariant random subgroups of strictly diagonal limits of finite symmetric groups. Bull. Lond. Math. Soc.
46(5) (2014), 1007–1020.Google Scholar
Tits, J.. Systemes générateurs de groupes de congruence. C. R. Acad. Sci. Paris AB
283(9) (1976), 693–695.Google Scholar
Tucker-Drob, R. D.. Weak equivalence and non-classifiability of measure preserving actions. Ergod. Th. & Dynam. Sys.
35(01) (2015), 293–336.Google Scholar
Vershik, A. M.. Totally nonfree actions and the infinite symmetric group. Mosc. Math. J.
12(1) (2012), 193–212, 216.Google Scholar