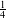Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-13T12:25:46.907Z Has data issue: false hasContentIssue false
  • English
  • Français

Hyperbolic rank rigidity for manifolds of $\frac{1}{4}$-pinched negative curvature

Part of: Global differential geometry Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  08 October 2018

CHRIS CONNELL ,
THANG NGUYEN  and
RALF SPATZIER
CHRIS CONNELL
Affiliation:
Department of Mathematics, Indiana University, Bloomington, IN 47405, USA email [email protected]
THANG NGUYEN
Affiliation:
Courant Institute of Mathematical Sciences, New York University, New York, NY 10012, USA email [email protected]
RALF SPATZIER
Affiliation:
Department of Mathematics, University of Michigan, Ann Arbor, MI 48109, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A Riemannian manifold 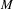$M$ has higher hyperbolic rank if every geodesic has a perpendicular Jacobi field making sectional curvature 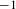$-1$ with the geodesic. If, in addition, the sectional curvatures of 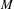$M$ lie in the interval 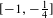$[-1,-\frac{1}{4}]$ and 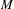$M$ is closed, we show that 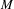$M$ is a locally symmetric space of rank one. This partially extends work by Constantine using completely different methods. It is also a partial counterpart to Hamenstädt’s hyperbolic rank rigidity result for sectional curvatures $\leq -1$, and complements well-known results on Euclidean and spherical rank rigidity.

Keywords

smooth dynamicsHamiltonian dynamicsgeodesic flowsrigidity

MSC classification

Primary: 53C24: Rigidity results
Secondary: 53C20: Global Riemannian geometry, including pinching 37D40: Dynamical systems of geometric origin and hyperbolicity (geodesic and horocycle flows, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 5 , May 2020 , pp. 1194 - 1216
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A. and Viana, M.. Extremal Lyapunov exponents: an invariance principle and applications. Invent. Math. 181 (2010), 115–178.Google Scholar
Avila, A., Santamaria, J. and Viana, M.. Holonomy invariance: rough regularity and applications to Lyapunov exponents. Astérisque 358 (2013), 13–74.Google Scholar
Ballmann, W.. Nonpositively curved manifolds of higher rank. Ann. of Math. (2) 122(3) (1985), 597–609.Google Scholar
Ballmann, W.. Lectures on Spaces of Nonpositive Curvature (DMV Seminar, 25). Birkhäuser, Basel, 1995, with an appendix by Misha Brin.Google Scholar
Ballmann, W., Brin, M. and Eberlein, P.. Structure of manifolds of nonpositive curvature. I. Ann. of Math. (2) 122(1) (1985), 171–203.Google Scholar
Benoist, Y., Foulon, P. and Labourie, F.. Flots d’Anosov à distributions de Liapounov différentiables. I. Hyperbolic behaviour of dynamical systems (Paris, 1990). Ann. Inst. H. Poincaré Phys. Théor. 53(4) (1990), 395–412.Google Scholar
Bettiol, R. G. and Schmidt, B.. Three-manifolds with many flat planes. Trans. Amer. Math. Soc. 370(1) (2018), 669–693.Google Scholar
Brin, M.. Ergodic theory of frame flows. Ergodic Theory and Dynamical Systems, II (College Park, MD, 1979/1980) (Progress in Mathematics, 21). Birkhäuser, Boston, MA, 1982, pp. 163–183.Google Scholar
Brown, A.. Smoothness of stable holonomies inside center-stable manifolds and the $C^{2}$ hypothesis in Pugh–Shub and Ledrappier–Young theory. Preprint, 2016, arXiv:1608.05886.Google Scholar
Burns, K. and Spatzier, R.. Manifolds of nonpositive curvature and their buildings. Publ. Math. Inst. Hautes Études Sci. 65 (1987), 35–59.Google Scholar
Burns, K. and Wilkinson, A.. A note on stable holonomy between centers. Preprint, 2005, http://www. math.northwestern.edu/∼burns/papers/bwilk2a/c1hol0611.pdf.Google Scholar
Butler, C.. Rigidity of equality of Lyapunov exponents for geodesic flows. J. Differential Geom. 109(1) (2018), 39–79.Google Scholar
Connell, C.. A characterization of homogeneous spaces with positive hyperbolic rank. Geom. Dedicata 93 (2002), 205–233.Google Scholar
Connell, C.. Minimal Lyapunov exponents, quasiconformal structures, and rigidity of non-positively curved manifolds. Ergod. Th. & Dynam. Sys. 23(2) (2003), 429–446.Google Scholar
Constantine, D.. 2-frame flow dynamics and hyperbolic rank-rigidity in nonpositive curvature. J. Mod. Dyn. 2(4) (2008), 719–740.Google Scholar
Eberlein, P. and Heber, J.. A differential geometric characterization of symmetric spaces of higher rank. Publ. Math. Inst. Hautes Études Sci. 71 (1990), 33–44.Google Scholar
Feres, R. and Katok, A.. Anosov flows with smooth foliations and rigidity of geodesic flows on three-dimensional manifolds of negative curvature. Ergod. Th. & Dynam. Sys. 10(4) (1990), 657–670.Google Scholar
Foulon, P.. Feuilletages des sphères et dynamiques Nord–Sud. C. R. Acad. Sci. Paris Sér. I Math. 318(11) (1994), 1041–1042.Google Scholar
Gallot, S., Hulin, D. and Lafontaine, J.. Riemannian Geometry (Universitext), 3rd edn. Springer, Berlin, 2004.Google Scholar
Hamenstädt, U.. Compact manifolds with 1/4-pinched negative curvature. Global Differential Geometry and Global Analysis (Lecture Notes in Mathematics, 1481). Eds. Ferus, D., Pinkall, U., Simon, U. and Wegner, B.. Springer, Berlin, 1991.Google Scholar
Hamenstädt, U.. A geometric characterization of negatively curved locally symmetric spaces. J. Differential Geom. 34(1) (1991), 193–221.Google Scholar
Hasselblatt, B.. Regularity of the Anosov splitting and of horospheric foliations. Ergod. Th. & Dynam. Sys. 14(4) (1994), 645–666.Google Scholar
Heintze, E. and Im Hof, C.. Geometry of horospheres. J. Differential Geom. 12(4) (1977), 481–491.Google Scholar
Hirsch, M. and Pugh, C.. Smoothness of horocycle foliations. J. Differential Geom. 10 (1975), 225–238.Google Scholar
Kanai, M.. Geodesic flows of negatively curved manifolds with smooth stable and unstable foliations. Ergod. Th. & Dynam. Sys. 8(2) (1988), 215–239.Google Scholar
Kalinin, B. and Sadovskaya, V.. Cocycles with one exponent over partially hyperbolic systems. Geom. Dedicata 167 (2013), 167–188.Google Scholar
Kalinin, B. and Sadovskaya, V.. Normal forms for non-uniform contractions. J. Mod. Dyn. 11(3) (2017), 341–368.Google Scholar
Lang, S.. Differential and Riemannian manifolds (Graduate Texts in Mathematics, 160), 3rd edn. Springer, New York, 1995.Google Scholar
Lin, S. and Schmidt, B.. Manifolds with many hyperbolic planes. Differential Geom. Appl. 52 (2017), 121–126.Google Scholar
Melnick, K.. Non-stationary smooth geometric structures for contracting measurable cocycles. Ergod. Th. & Dynam. Sys. (2017), doi:10.1017/etds.2017.38. Published online 28 June 2017.Google Scholar
Spatzier, R. J. and Strake, M.. Some examples of higher rank manifolds of nonnegative curvature. Comment. Math. Helv. 65(2) (1990), 299–317.Google Scholar
Schmidt, B., Shankar, K. and Spatzier, R.. Positively curved manifolds with large spherical rank. Comment. Math. Helv. 91(2) (2016), 219–251.Google Scholar
Shankar, K., Spatzier, R. and Wilking, B.. Spherical rank rigidity and Blaschke manifolds. Duke Math. J. 128(1) (2005), 65–81.Google Scholar
Watkins, J.. The higher rank rigidity theorem for manifolds with no focal points. Geom. Dedicata 164 (2013), 319–349.Google Scholar