No CrossRef data available.
Published online by Cambridge University Press: 28 September 2017
The orbit closure of any translation surface under the horocycle flow in almost any direction equals its 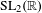 $\text{SL}_{2}(\mathbb{R})$ orbit closure. This result gives rise to new characterizations of lattice surfaces in terms of the horocycle flow.
$\text{SL}_{2}(\mathbb{R})$ orbit closure. This result gives rise to new characterizations of lattice surfaces in terms of the horocycle flow.