Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T04:10:00.698Z Has data issue: false hasContentIssue false
  • English
  • Français

A Herman–Avila–Bochi formula for higher-dimensional pseudo-unitary and Hermitian-symplectic cocycles

Published online by Cambridge University Press:  14 March 2014

CHRISTIAN SADEL
CHRISTIAN SADEL*
Affiliation:
University of British Columbia, 1984 Mathematics Road, Vancouver, BC, CanadaV6T 1Z2 email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A Herman–Avila–Bochi type formula is obtained for the average sum of the top 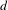$d$ Lyapunov exponents over a one-parameter family of 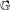$\mathbb{G}$-cocycles, where $\mathbb{G}$ is the group that leaves a certain, non-degenerate Hermitian form of signature 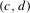$(c,d)$ invariant. The generic example of such a group is the pseudo-unitary group 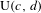$\text{U}(c,d)$ or, in the case 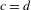$c=d$, the Hermitian-symplectic group 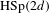$\text{HSp}(2d)$ which naturally appears for cocycles related to Schrödinger operators. In the case 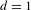$d=1$, the formula for 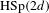$\text{HSp}(2d)$ cocycles reduces to the Herman–Avila–Bochi formula for 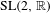$\text{SL}(2,\mathbb{R})$ cocycles.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 5 , August 2015 , pp. 1582 - 1591
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A.. Density of positive Lyapunov exponents for SL(2, ℝ)-cocycles. J. Amer. Math. Soc. 24 (2011), 999–1014.CrossRefGoogle Scholar
Avila, A. and Bochi, J.. A formula with some applications to the theory of Lyapunov exponents. Israel J. Math. 131 (2002), 125–137.CrossRefGoogle Scholar
Avila, A., Jitomirskaya, S. and Sadel, C.. Complex one-frequency cocycles. J. Eur. Math. Soc. to appear. Preprint, 2013, arXiv:1306.1605.CrossRefGoogle Scholar
Baraviera, A., Dias, J. and Duarte, P.. On the Herman–Avila–Bochi formula for Lyapunov exponents of SL(2, ℝ) cocycles. Nonlinearity 24 (2011), 2465.CrossRefGoogle Scholar
Duarte, P. and Klein, S.. Positive Lyapunov exponents for higher dimensional quasiperiodic cocycles. Preprint, 2012, arXiv:1211.4002.Google Scholar
Duarte, P. and Klein, S.. Continuity of the Lyapunov exponents for quasiperiodic cocycles. Commun. Math. Phys. to appear. Preprint, 2013, arXiv:1305.7504.CrossRefGoogle Scholar
Haro, A. and Puig, J.. A Thouless formula and Aubry duality for long-range Schrödinger skew-products. Nonlinearity 26 (2013), 1163–1187.CrossRefGoogle Scholar
Herman, M.. Une méthode pour minorer les exposants de Lyapounov et quelques exemples montrant le caractère local d’un théorème d’Arnold et de Moser sur le tore de dimension 2. Comment. Math. Helv. 58 (1983), 453–502.CrossRefGoogle Scholar
Schlag, W.. Regularity and convergence rates for the Lyapunov exponents of linear co-cycles. Preprint, 2012, arXiv:1211.0648.Google Scholar
Schulz-Baldes, H.. Geometry of Weyl theory for Jacobi matrices with matrix entries. J. d’ Analyse Math. 110 (2010), 129–165.CrossRefGoogle Scholar