Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-24T18:50:53.897Z Has data issue: false hasContentIssue false
  • English
  • Français

Hausdorff dimension of multidimensional multiplicative subshifts

Part of: Smooth dynamical systems: general theory Classical measure theory

Published online by Cambridge University Press:  19 July 2023

JUNG-CHAO BAN ,
WEN-GUEI HU  and
GUAN-YU LAI Open the ORCID record for GUAN-YU LAI [Opens in a new window]
JUNG-CHAO BAN
Affiliation:
Department of Mathematical Sciences, National Chengchi University, Taipei 11605, Taiwan, ROC Math. Division, National Center for Theoretical Science, National Taiwan University, Taipei 10617, Taiwan, ROC (e-mail: [email protected])
WEN-GUEI HU
Affiliation:
College of Mathematics, Sichuan University, Chengdu 610064, China (e-mail: [email protected])
GUAN-YU LAI*
Affiliation:
Department of Mathematical Sciences, National Chengchi University, Taipei 11605, Taiwan, ROC
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The purpose of this study is two-fold. First, the Hausdorff dimension formula of the multidimensional multiplicative subshift (MMS) in 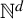$\mathbb {N}^d$ is presented. This extends the earlier work of Kenyon et al [Hausdorff dimension for fractals invariant under multiplicative integers. Ergod. Th. & Dynam. Sys. 32(5) (2012), 1567–1584] from 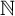$\mathbb {N}$ to 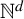$\mathbb {N}^d$. In addition, the preceding work of the Minkowski dimension of the MMS in 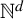$\mathbb {N}^d$ is applied to show that their Hausdorff dimension is strictly less than the Minkowski dimension. Second, the same technique allows us to investigate the multifractal analysis of multiple ergodic average in 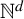$\mathbb {N}^d$. Precisely, we extend the result of Fan et al, [Multifractal analysis of some multiple ergodic averages. Adv. Math. 295 (2016), 271–333] of the multifractal analysis of multiple ergodic average from 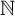$\mathbb {N}$ to 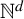$\mathbb {N}^d$.

Keywords

multiplicative subshiftsmultiple ergodic averagesHausdorff dimensionmultifractal analysis

MSC classification

Primary: 28A80: Fractals 37C45: Dimension theory of dynamical systems 28A78: Hausdorff and packing measures
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 44 , Issue 5 , May 2024 , pp. 1239 - 1268
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ban, J. C., Hu, W. G. and Lai, G. Y.. On the entropy of multidimensional multiplicative integer subshifts. J. Stat. Phys. 182(2) (2021), 1–20.10.1007/s10955-021-02703-7CrossRefGoogle Scholar
Ban, J. C., Hu, W. G. and Lai, G. Y.. Large deviation principle of multidimensional multiple averages on ${\mathbb{N}}^d$ . Indag. Math. (N.S.) 33 (2022), 450–471.10.1016/j.indag.2021.09.010CrossRefGoogle Scholar
Ban, J. C., Hu, W. G. and Lin, S. S.. Pattern generation problems arising in multiplicative integer systems. Ergod. Th. & Dynam. Sys. 39(5) (2019), 1234–1260.10.1017/etds.2017.74CrossRefGoogle Scholar
Billingsley, P.. Ergodic Theory and Information. Wiley, New York, 1965.Google Scholar
Bourgain, J.. Double recurrence and almost sure convergence. J. Reine Angew. Math. 404 (1990), 140–161.Google Scholar
Brunet, G.. Dimensions of ‘self-affine sponges’ invariant under the action of multiplicative integers. Ergod. Th. & Dynam. Sys. 43 (2021), 417–459.10.1017/etds.2021.155CrossRefGoogle Scholar
Conze, J. P. and Lesigne, E.. Théorèmes ergodiques pour des mesures diagonales. Bull. Soc. Math. France 112 (1984), 143–175.10.24033/bsmf.2003CrossRefGoogle Scholar
Fan, A. H.. Sur les dimensions de mesures. Studia Math. 111 (1994), 1–17.10.4064/sm-111-1-1-17CrossRefGoogle Scholar
Fan, A. H.. Some aspects of multifractal analysis. Geometry and Analysis of Fractals. Eds. Feng, D.-J. and Lau, K.-S.. Springer, Berlin, 2014, pp. 115–145.10.1007/978-3-662-43920-3_5CrossRefGoogle Scholar
Fan, A. H., Liao, L. M. and Ma, J. H.. Level sets of multiple ergodic averages. Monatsh. Math. 168(1) (2012), 17–26.10.1007/s00605-011-0358-5CrossRefGoogle Scholar
Fan, A. H., Schmeling, J. and Wu, M.. Multifractal analysis of some multiple ergodic averages. Adv. Math. 295 (2016), 271–333.10.1016/j.aim.2016.03.012CrossRefGoogle Scholar
Frantzikinakis, N.. Some open problems on multiple ergodic averages. Preprint, 2016, arXiv:1103.3808.Google Scholar
Furstenberg, H., Katznelson, Y. and Ornstein, D.. The ergodic theoretical proof of Szemerédi’s theorem. Bull. Amer. Math. Soc. (N.S.) 7(3) (1982), 527–552.10.1090/S0273-0979-1982-15052-2CrossRefGoogle Scholar
Gutman, Y., Huang, W., Shao, S. and Ye, X. D.. Almost sure convergence of the multiple ergodic average for certain weakly mixing systems. Acta Math. Sin. (Engl. Ser.) 34 (2018), 79–90.10.1007/s10114-017-6366-1CrossRefGoogle Scholar
Host, B. and Kra, B.. Nonconventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161 (2005), 397–488.10.4007/annals.2005.161.397CrossRefGoogle Scholar
Kenyon, R., Peres, Y. and Solomyak, B.. Hausdorff dimension for fractals invariant under multiplicative integers. Ergod. Th. & Dynam. Sys. 32(5) (2012), 1567–1584.10.1017/S0143385711000538CrossRefGoogle Scholar
Peres, Y., Schmeling, J., Seuret, S. and Solomyak, B.. Dimensions of some fractals defined via the semigroup generated by 2 and 3. Israel J. Math. 199(2) (2014), 687–709.10.1007/s11856-013-0058-zCrossRefGoogle Scholar
Peres, Y. and Solomyak, B.. Dimension spectrum for a nonconventional ergodic average. Real Anal. Exchange 37(2) (2012), 375–388.10.14321/realanalexch.37.2.0375CrossRefGoogle Scholar
Pollicott, M.. A nonlinear transfer operator theorem. J. Stat. Phys. 166(3–4) (2017), 516–524.10.1007/s10955-016-1646-1CrossRefGoogle ScholarPubMed
Wu, M.. Analyses multifractales de certaines moyennes ergodiques non-conventionnelles. PhD Thesis, L’Universit’e de Picardie Jules Verne, 2013.Google Scholar