Article contents
A global two-dimensional version of Smale’s cancellation theorem via spectral sequences
Published online by Cambridge University Press: 19 March 2015
Abstract
In this article, Conley’s connection matrix theory and a spectral sequence analysis of a filtered Morse chain complex 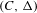 $(C,{\rm\Delta})$ are used to study global continuation results for flows on surfaces. The briefly described unfoldings of Lyapunov graphs have been proved to be a well-suited combinatorial tool to keep track of continuations. The novelty herein is a global dynamical cancellation theorem inferred from the differentials of the spectral sequence
$(C,{\rm\Delta})$ are used to study global continuation results for flows on surfaces. The briefly described unfoldings of Lyapunov graphs have been proved to be a well-suited combinatorial tool to keep track of continuations. The novelty herein is a global dynamical cancellation theorem inferred from the differentials of the spectral sequence 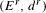 $(E^{r},d^{r})$. The local version of this theorem relates differentials
$(E^{r},d^{r})$. The local version of this theorem relates differentials 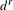 $d^{r}$ of the
$d^{r}$ of the  $r$th page
$r$th page 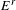 $E^{r}$ to Smale’s theorem on cancellation of critical points.
$E^{r}$ to Smale’s theorem on cancellation of critical points.
- Type
- Research Article
- Information
- Copyright
- © Cambridge University Press, 2015
References
- 3
- Cited by


