Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-27T05:47:14.747Z Has data issue: false hasContentIssue false
  • English
  • Français

Glider automata on all transitive sofic shifts

Part of: Topological dynamics

Published online by Cambridge University Press:  30 September 2021

JOHAN KOPRA Open the ORCID record for JOHAN KOPRA [Opens in a new window]
JOHAN KOPRA*
Affiliation:
Department of Mathematics and Statistics, University of Turku, FI-20014 Turku, Finland
*
(e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

For any infinite transitive sofic shift X we construct a reversible cellular automaton (that is, an automorphism of the shift X) which breaks any given finite point of the subshift into a finite collection of gliders traveling into opposing directions. This shows in addition that every infinite transitive sofic shift has a reversible cellular automaton which is sensitive with respect to all directions. As another application we prove a finitary version of Ryan’s theorem: the automorphism group 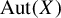$\operatorname {\mathrm {Aut}}(X)$ contains a two-element subset whose centralizer consists only of shift maps. We also show that in the class of S-gap shifts these results do not extend beyond the sofic case.

Keywords

sofic shiftssynchronized shiftscellular automataautomorphisms

MSC classification

Primary: 37B10: Symbolic dynamics
Secondary: 37B15: Cellular automata
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 12 , December 2022 , pp. 3716 - 3744
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bertrand, A.. Specification, synchronisation, average length. International Colloquium on Coding Theory and Applications. Springer, Berlin, 1986, pp. 86–95.Google Scholar
Boyle, M.. Open problems in symbolic dynamics. Contemp. Math. 469 (2008), 69–118.CrossRefGoogle Scholar
Boyle, M., Lind, D. and Rudolph, D.. The automorphism group of a shift of finite type. Trans. Amer. Math. Soc. 306(1) (1988), 71–114.CrossRefGoogle Scholar
Dastjerdi, D. A. and Jangjoo, S.. Dynamics and topology of S-gap shifts. Topology Appl. 159(10–11) (2012), 2654–2661.CrossRefGoogle Scholar
Fiebig, D. and Fiebig, U.-R.. Covers for coded systems. Contemp. Math. 135 (1992), 139–179.Google Scholar
Fiebig, D. and Fiebig, U.-R.. The automorphism group of a coded system. Trans. Amer. Math. Soc. 348(8) (1996), 3173–3191.CrossRefGoogle Scholar
Hedlund, G. A.. Endomorphisms and automorphisms of the shift dynamical system. Math. Syst. Theory 3(4) (1969), 320–375.CrossRefGoogle Scholar
Jonoska, N.. Sofic shifts with synchronizing presentations. Theoret. Comput. Sci. 158(1–2) (1996), 81–115.CrossRefGoogle Scholar
Jung, U.. On the existence of open and bi-continuing codes. Trans. Amer. Math. Soc. 363(3) (2011), 1399–1417.CrossRefGoogle Scholar
Kitchens, B. P.. Symbolic Dynamics: One-Sided, Two-Sided and Countable State Markov Shifts. Springer, Berlin, 1997.Google Scholar
Kopra, J.. Cellular automata with complicated dynamics. PhD Thesis, University of Turku, 2019.Google Scholar
Kopra, J.. Glider automorphisms and a finitary Ryan’s theorem for transitive subshifts of finite type. Nat. Comput. 19 (2019), 773–786.CrossRefGoogle Scholar
Kopra, J.. Dynamics of cellular automata on beta-shifts and direct topological factorizations. Developments in Language Theory: 24th International Conference (Lecture Notes in Computer Science, 12086). Springer, Cham, 2020, pp. 178–191.CrossRefGoogle Scholar
Lind, D. A.. The entropies of topological Markov shifts and a related class of algebraic integers. Ergod. Th. & Dynam. Sys. 4(2) (1984), 283–300.CrossRefGoogle Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Pin, J. E.. Varieties of Formal Languages. Plenum, New York, 1986.CrossRefGoogle Scholar
Ryan, J. P.. The shift and commutativity. Math. Syst. Theory 6 (1972), 82–85.CrossRefGoogle Scholar
Ryan, J. P.. The shift and commutivity II. Math. Syst. Theory 8(3) (1974/75), 249–250.CrossRefGoogle Scholar
Sablik, M.. Directional dynamics for cellular automata: a sensitivity to initial condition approach. Theoret. Comput. Sci. 400(1–3) (2008), 1–18.CrossRefGoogle Scholar
Salo, V.. Transitive action on finite points of a full shift and a finitary Ryan’s theorem. Ergod. Th. & Dynam. Sys. 39(6) (2019), 1637–1667.CrossRefGoogle Scholar
Salo, V. and Törmä, I.. A one-dimensional physically universal cellular automaton. Unveiling Dynamics and Complexity: Conference on Computability in Europe. Springer, Cham, 2017, pp. 375–386.CrossRefGoogle Scholar
Yang, K.. Normal amenable subgroups of the automorphism group of sofic shifts. Ergod. Th. & Dynam. Sys. 41(4) (2020), 1250–1263.CrossRefGoogle Scholar