Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Lacomba, Ernesto A.
and
Sienra, Guillermo
1988.
Holomorphic Dynamics.
Vol. 1345,
Issue. ,
p.
177.
Roussarie, R
1989.
Finite cyclicity of loops and cusps.
Nonlinearity,
Vol. 2,
Issue. 1,
p.
73.
Li, Chengzhi
and
Rousseau, Christiane
1989.
A system with three limit cycles appearing in a Hopf bifurcation and dying in a homoclinic bifurcation: The cusp of order 4.
Journal of Differential Equations,
Vol. 79,
Issue. 1,
p.
132.
Chua, L.O.
and
Kokubu, H.
1989.
Normal forms for nonlinear vector fields. II. Applications.
IEEE Transactions on Circuits and Systems,
Vol. 36,
Issue. 1,
p.
51.
Joyal, Pierre
and
Rousseau, Christiane
1989.
Saddle quantities and applications.
Journal of Differential Equations,
Vol. 78,
Issue. 2,
p.
374.
Joyal, Pierre
1990.
The cusp of order N.
Journal of Differential Equations,
Vol. 88,
Issue. 1,
p.
1.
McCaughan, F. E.
1990.
Bifurcation Analysis of Axial Flow Compressor Stability.
SIAM Journal on Applied Mathematics,
Vol. 50,
Issue. 5,
p.
1232.
Dumortier, Freddy
and
Roussarie, Robert
1990.
Bifurcations of Planar Vector Fields.
Vol. 1455,
Issue. ,
p.
44.
Rousseau, Christiane
1990.
Bifurcations of Planar Vector Fields.
Vol. 1455,
Issue. ,
p.
334.
Mardešić, P.
1990.
The number of limit cycles of polynomial deformations of a Hamiltonian vector field.
Ergodic Theory and Dynamical Systems,
Vol. 10,
Issue. 3,
p.
523.
Denkowska, Zofia
and
Roussarie, Robert
1991.
A method of desingularization for analytic two-dimensional vector field families.
Boletim da Sociedade Brasileira de Matem�tica,
Vol. 22,
Issue. 1,
p.
93.
Dumortier, Freddy
and
Fiddelaers, Peter
1991.
Quadratic models for generic local 3-parameter bifurcations on the plane.
Transactions of the American Mathematical Society,
Vol. 326,
Issue. 1,
p.
101.
Baesens, C.
Guckenheimer, J.
Kim, S.
and
MacKay, R.S.
1991.
Three coupled oscillators: mode-locking, global bifurcations and toroidal chaos.
Physica D: Nonlinear Phenomena,
Vol. 49,
Issue. 3,
p.
387.
Dumortier, Freddy
Roussarie, Robert
Sotomayor, Jorge
and
Żaładek, Henryk
1991.
Bifurcations of Planar Vector Fields.
Vol. 1480,
Issue. ,
p.
135.
Dumortier, F.
1991.
Structures in Dynamics - Finite Dimensional Deterministic Studies.
Vol. 2,
Issue. ,
p.
161.
Dumortier, Freddy
Roussarie, Robert
Sotomayor, Jorge
and
Żaładek, Henryk
1991.
Bifurcations of Planar Vector Fields.
Vol. 1480,
Issue. ,
p.
165.
Baider, Alberto
and
Sanders, Jan A
1992.
Further reduction of the Takens-Bogdanov normal form.
Journal of Differential Equations,
Vol. 99,
Issue. 2,
p.
205.
Rothe, Franz
and
Shafer, Douglas S.
1992.
Multiple bifurcation in a predator–prey system with nonmonotonic predator response.
Proceedings of the Royal Society of Edinburgh: Section A Mathematics,
Vol. 120,
Issue. 3-4,
p.
313.
Zhi-Fen, Zhang
and
Bao-Yi, Li
1992.
High order Melnikov functions and the problem of uniformity in global bifurcation.
Annali di Matematica Pura ed Applicata (1923 -),
Vol. 161,
Issue. 1,
p.
181.
Clarke, Bruce L.
and
Jiang, Weimin
1993.
Method for deriving Hopf and saddle-node bifurcation hypersurfaces and application to a model of the Belousov–Zhabotinskii system.
The Journal of Chemical Physics,
Vol. 99,
Issue. 6,
p.
4464.


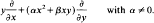
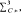 consisting of germs of cusp type whose 4-jet is
consisting of germs of cusp type whose 4-jet is 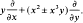
 transversally in (0, 0) is fibre-
transversally in (0, 0) is fibre-