Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T04:29:37.857Z Has data issue: false hasContentIssue false
  • English
  • Français

Garden of Eden and specification

Published online by Cambridge University Press:  13 March 2018

HANFENG LI
HANFENG LI*
Affiliation:
Center of Mathematics, Chongqing University, Chongqing 401331, China Department of Mathematics, SUNY at Buffalo, Buffalo, NY 14260-2900, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We establish a Garden of Eden theorem for expansive algebraic actions of amenable groups with the weak specification property, i.e. for any continuous equivariant map $T$ from the underlying space to itself, $T$ is pre-injective if and only if it is surjective. In particular, this applies to all expansive principal algebraic actions of amenable groups and expansive algebraic actions of 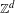$\mathbb{Z}^{d}$ with completely positive entropy.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 11 , November 2019 , pp. 3075 - 3088
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bartholdi, L.. Gardens of Eden and amenability on cellular automata. J. Eur. Math. Soc. (JEMS) 12(1) (2010), 241–248.10.4171/JEMS/196Google Scholar
Bartholdi, L.. Amenability of groups is characterized by Myhill’s theorem. J. Eur. Math. Soc. to appear. Preprint, 2016, arXiv:1605.09133, with an appendix by D. Kielak.Google Scholar
Bowen, R.. Periodic points and measures for Axiom A diffeomorphisms. Trans. Amer. Math. Soc. 154 (1971), 377–397.Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. Cellular Automata and Groups (Springer Monographs in Mathematics) . Springer, Berlin, 2010.10.1007/978-3-642-14034-1Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. The Myhill property for strongly irreducible subshifts over amenable groups. Monatsh. Math. 165(2) (2012), 155–172.10.1007/s00605-010-0256-2Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. Expansive actions of countable amenable groups, homoclinic pairs, and the Myhill property. Illinois J. Math. 59(3) (2015), 597–621.10.1215/ijm/1475266399Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. A garden of Eden theorem for Anosov diffeomorphisms on tori. Topology Appl. 212 (2016), 49–56.10.1016/j.topol.2016.08.025Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. A Garden of Eden theorem for principal algebraic actions. Preprint, 2017, arXiv:1706.06548.Google Scholar
Ceccherini-Silberstein, T. and Coornaert, M.. The Garden of Eden theorem: old and new. Handbook of Group Actions (Advanced Lectures in Mathematics) . Eds. Ji, L., Paradopoulos, A. and Yau, S.-T.. International Press, Somerville, MA, to appear. Preprint, 2017, arXiv:1707.08898.Google Scholar
Ceccherini-Silberstein, T., Machì, A. and Scarabotti, F.. Amenable groups and cellular automata. Ann. Inst. Fourier (Grenoble) 49(2) (1999), 673–685.10.5802/aif.1686Google Scholar
Chung, N. and Li, H.. Homoclinic groups, IE groups, and expansive algebraic actions. Invent. Math. 199(3) (2015), 805–858.10.1007/s00222-014-0524-1Google Scholar
Deninger, C.. Fuglede–Kadison determinants and entropy for actions of discrete amenable groups. J. Amer. Math. Soc. 19 (2006), 737–758.10.1090/S0894-0347-06-00519-4Google Scholar
Deninger, C. and Schmidt, K.. Expansive algebraic actions of discrete residually finite amenable groups and their entropy. Ergod. Th. & Dynam. Sys. 27 (2007), 769–786.10.1017/S0143385706000939Google Scholar
Fiorenzi, F.. The Garden of Eden theorem for sofic shifts. Pure Math. Appl. 11(3) (2000), 471–484.Google Scholar
Fiorenzi, F.. Cellular automata and strongly irreducible shifts of finite type. Theoret. Comput. Sci. 299(1–3) (2003), 477–493.10.1016/S0304-3975(02)00492-9Google Scholar
Gottschalk, W.. Some general dynamical notions. Recent Advances in Topological Dynamics (Lecture Notes in Mathematics, 318) . Springer, Berlin, 1973, pp. 120–125.10.1007/BFb0061728Google Scholar
Gromov, M.. Endomorphisms of symbolic algebraic varieties. J. Eur. Math. Soc. (JEMS) 1(2) (1999), 109–197.10.1007/PL00011162Google Scholar
Kerr, D. and Li, H.. Combinatorial independence and sofic entropy. Commun. Math. Stat. 1(2) (2013), 213–257.10.1007/s40304-013-0001-yGoogle Scholar
Kerr, D. and Li, H.. Ergodic Theory: Independence and Dichotomies (Springer Monographs in Mathematics) . Springer, Cham, 2016.10.1007/978-3-319-49847-8Google Scholar
Lind, D. and Schmidt, K.. Homoclinic points of algebraic ℤ d -actions. J. Amer. Math. Soc. 12(4) (1999), 953–980.10.1090/S0894-0347-99-00306-9Google Scholar
Machì, A. and Mignosi, F.. Garden of Eden configurations for cellular automata on Cayley graphs of groups. SIAM J. Discrete Math. 6(1) (1993), 44–56.10.1137/0406004Google Scholar
Moore, E. F.. Machine models of self-reproduction. Mathematical Problems in the Biological Sciences (Proceedings of Symposia in Applied Mathematics, 14) . American Mathematical Society, Providence, RI, 1963, pp. 17–34.Google Scholar
Moulin Ollagnier, J.. Ergodic Theory and Statistical Mechanics (Lecture Notes in Mathematics, 1115) . Springer, Berlin, 1985.10.1007/BFb0101575Google Scholar
Myhill, J.. The converse of Moore’s Garden-of-Eden theorem. Proc. Amer. Math. Soc. 14 (1963), 685–686.Google Scholar
Ren, X.. Periodic measures are dense in invariant measures for residually finite amenable group actions with specification. Discrete Contin. Dyn. Syst. 38(4) (2018), 1657–1667.10.3934/dcds.2018068Google Scholar
Ruelle, D.. Statistical mechanics on a compact set with Z v action satisfying expansiveness and specification. Trans. Amer. Math. Soc. 187 (1973), 237–251.10.2307/1996437Google Scholar
Schmidt, K.. Dynamical Systems of Algebraic Origin (Progress in Mathematics, 128) . Birkhäuser, Basel, 1995.Google Scholar
Walters, P.. An Introduction to Ergodic Theory (Graduate Texts in Mathematics, 79) . Springer, New York, 1982.10.1007/978-1-4612-5775-2Google Scholar
Weiss, B.. Sofic groups and dynamical systems. Ergodic Theory and Harmonic Analysis (Mumbai, 1999) Sankhyā Ser. A 62 (2000), 350–359.Google Scholar