Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-10T19:17:30.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Flows, growth rates, and the veering polynomial

Part of: Low-dimensional topology Dynamical systems with hyperbolic behavior Smooth dynamical systems: general theory

Published online by Cambridge University Press:  04 October 2022

MICHAEL P. LANDRY Open the ORCID record for MICHAEL P. LANDRY [Opens in a new window] ,
YAIR N. MINSKY Open the ORCID record for YAIR N. MINSKY [Opens in a new window]  and
SAMUEL J. TAYLOR Open the ORCID record for SAMUEL J. TAYLOR [Opens in a new window]
MICHAEL P. LANDRY*
Affiliation:
Department of Mathematics and Statistics, Washington University in Saint Louis, St. Louis, MO 63130, USA
YAIR N. MINSKY
Affiliation:
Department of Mathematics, Yale University, New Haven, CT 06520, USA (e-mail: [email protected])
SAMUEL J. TAYLOR
Affiliation:
Department of Mathematics, Temple University, Philadelphia, PA 19122, USA (e-mail: [email protected])
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a pseudo-Anosov flow 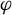$\varphi $ without perfect fits on a closed 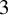$3$-manifold, Agol–Guéritaud produce a veering triangulation 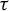$\tau $ on the manifold M obtained by deleting the singular orbits of 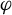$\varphi $. We show that 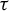$\tau $ can be realized in M so that its 2-skeleton is positively transverse to 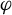$\varphi $, and that the combinatorially defined flow graph 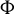$\Phi $ embedded in M uniformly codes the orbits of 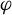$\varphi $ in a precise sense. Together with these facts, we use a modified version of the veering polynomial, previously introduced by the authors, to compute the growth rates of the closed orbits of 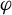$\varphi $ after cutting M along certain transverse surfaces, thereby generalizing the work of McMullen in the fibered setting. These results are new even in the case where the transverse surface represents a class in the boundary of a fibered cone of M. Our work can be used to study the flow 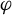$\varphi $ on the original closed manifold. Applications include counting growth rates of closed orbits after cutting along closed transverse surfaces, defining a continuous, convex entropy function on the ‘positive’ cone in 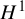$H^1$ of the cut-open manifold, and answering a question of Leininger about the closure of the set of all stretch factors arising as monodromies within a single fibered cone of a 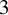$3$-manifold. This last application connects to the study of endperiodic automorphisms of infinite-type surfaces and the growth rates of their periodic points.

Keywords

low-dimensional dynamicstopological dynamicssymbolic dynamicsgroup actions

MSC classification

Primary: 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.) 37C27: Periodic orbits of vector fields and flows 57M60: Group actions in low dimensions
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 43 , Issue 9 , September 2023 , pp. 3026 - 3107
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agol, I.. Criteria for virtual fibering. J. Topol. 1(2) (2008), 269–284.10.1112/jtopol/jtn003CrossRefGoogle Scholar
Agol, I.. Ideal triangulations of pseudo-Anosov mapping tori. Topology and Geometry in Dimension Three (Contemporary Mathematics, 560). Eds. W. Li, L. Bartolini, J. Johnson, F. Luo, R. Myers and J. Hyam Rubinstein. American Mathematical Society, Providence, RI, 2011, pp. 1–17.Google Scholar
Anosov, D. V.. Ergodic properties of geodesic flows on closed Riemannian manifolds of negative curvature. Dokl. Akad. Nauk SSSR 151 (1963), 1250–1252.Google Scholar
Agol, I. and Tsang, C. C.. Dynamics of veering triangulations: infinitesimal components of their flow graphs and applications. Preprint, 2022, arXiv:2201.02706.Google Scholar
Cooper, D., Long, D. D. and Reid, A. W.. Bundles and finite foliations. Invent. Math. 118(1) (1994), 255–283.CrossRefGoogle Scholar
Fenley, S. R.. Asymptotic properties of depth one foliations in hyperbolic 3-manifolds. J. Differential Geom. 36(2) (1992), 269–313.CrossRefGoogle Scholar
Fenley, S.. Foliations with good geometry. J. Amer. Math. Soc. 12(3) (1999), 619–676.CrossRefGoogle Scholar
Fenley, S. R.. Surfaces transverse to pseudo-Anosov flows and virtual fibers in 3-manifolds. Topology 38(4) (1999), 823–859.10.1016/S0040-9383(98)00030-5CrossRefGoogle Scholar
Fenley, S. R.. Pseudo-Anosov flows and incompressible tori. Geom. Dedicata. 99(1) (2003), 61–102.CrossRefGoogle Scholar
Fenley, S.. Ideal boundaries of pseudo-Anosov flows and uniform convergence groups with connections and applications to large scale geometry. Geom. Topol. 16(1) (2012), 1–110.10.2140/gt.2012.16.1CrossRefGoogle Scholar
Futer, D. and Guéritaud, F.. Explicit angle structures for veering triangulations. Algebr. Geom. Topol. 13(1) (2013), 205–235.CrossRefGoogle Scholar
Fenley, S. and Mosher, L.. Quasigeodesic flows in hyperbolic 3-manifolds. Topology 40(3) (2001), 503–537.10.1016/S0040-9383(99)00072-5CrossRefGoogle Scholar
Floyd, W. and Oertel, U.. Incompressible surfaces via branched surfaces. Topology 23(1) (1984), 117–125.CrossRefGoogle Scholar
Fried, D.. Fibrations over ${S}^1$ with pseudo-Anosov monodromy. Travaux de Thurston sur les surfaces (Astérisque, 66–67). Eds. A. Fathi, F. Laudenbach and V. Poénaru. Société mathématique de France, Paris, 1979, pp. 251–266 (translated to English by D. Kim and D. Margalit).Google Scholar
Fried, D.. Flow equivalence, hyperbolic systems and a new zeta function for flows. Comment. Math. Helv. 57(1) (1982), 237–259.10.1007/BF02565860CrossRefGoogle Scholar
Fried, D.. The geometry of cross sections to flows. Topology 21(4) (1982), 353–371.10.1016/0040-9383(82)90017-9CrossRefGoogle Scholar
Futer, D., Taylor, S. J. and Worden, W.. Random veering triangulations are not geometric. Groups Geom. Dyn. 14(3) (2020), 1077–1126.10.4171/GGD/575CrossRefGoogle Scholar
Fulton, W.. Introduction to Toric Varieties (Annals of Mathematics Studies, 131). Princeton University Press, Princeton, NJ, 1993.10.1515/9781400882526CrossRefGoogle Scholar
Gabai, D. and Oertel, U.. Essential laminations in 3-manifolds. Ann. of Math. (2) 130(1) (1989), 41–73.CrossRefGoogle Scholar
Griebenow, R.. Personnel Communication, 2022.Google Scholar
Guéritaud, F.. Veering triangulations and Cannon–Thurston maps. J. Topol. 9(3) (2016), 957–983.CrossRefGoogle Scholar
Hironaka, E.. Small dilatation mapping classes coming from the simplest hyperbolic braid. Algebr. Geom. Topol. 10(4) (2010), 2041–2060.10.2140/agt.2010.10.2041CrossRefGoogle Scholar
Hodgson, C. D., Issa, A. and Segerman, H.. Non-geometric veering triangulations. Exp. Math. 25(1) (2016), 17–45.10.1080/10586458.2015.1005256CrossRefGoogle Scholar
Hodgson, C. D., Hyam Rubinstein, J., Segerman, H. and Tillmann, S.. Veering triangulations admit strict angle structures. Geom. Topol. 15(4) (2011), 2073–2089.CrossRefGoogle Scholar
Kin, E., Kojima, S. and Takasawa, M.. Minimal dilatations of pseudo-Anosovs generated by the magic 3-manifold and their asymptotic behavior. Algebr. Geom. Topol. 13(6) (2013), 3537–3602.10.2140/agt.2013.13.3537CrossRefGoogle Scholar
Lackenby, M.. Taut ideal triangulations of 3-manifolds. Geom. Topol. 4(1) (2000), 369–395.10.2140/gt.2000.4.369CrossRefGoogle Scholar
Landry, M.. Taut branched surfaces from veering triangulations. Algebr. Geom. Topol. 18(2) (2018), 1089–1114.CrossRefGoogle Scholar
Landry, M.. Stable loops and almost transverse surfaces. Groups Geom. Dynam., to appear.Google Scholar
Landry, M.. Veering triangulations and the Thurston norm: homology to isotopy. Adv. Math. 396 (2022), 108102.10.1016/j.aim.2021.108102CrossRefGoogle Scholar
Leininger, C. J. and Margalit, D.. On the number and location of short geodesics in moduli space. J. Topol. 6(1) (2013), 30–48.CrossRefGoogle Scholar
Landry, M., Minsky, Y. and Taylor, S.. A polynomial invariant for veering triangulations. Preprint, 2020, arXiv:2008.04836.Google Scholar
Landry, M., Minsky, Y. N. and Taylor, S. J.. Endperiodic maps via pseudo-anosov flows, in preparation.Google Scholar
McMullen, C. T.. Polynomial invariants for fibered 3-manifolds and Teichmüller geodesics for foliations. Ann. Sci. Éc. Norm. Supér. (4) 33(4) (2000), 519–560.10.1016/S0012-9593(00)00121-XCrossRefGoogle Scholar
McMullen, C. T.. Entropy and the clique polynomial. J. Topol. 8(1) (2015), 184–212.10.1112/jtopol/jtu022CrossRefGoogle Scholar
Mosher, L.. Dynamical systems and the homology norm of a $3$ -manifold I: efficient intersection of surfaces and flows. Duke Math. J. 65(3) (1992), 449–500.10.1215/S0012-7094-92-06518-5CrossRefGoogle Scholar
Mosher, L.. Dynamical systems and the homology norm of a 3-manifold II. Invent. Math. 107(1) (1992), 243–281.CrossRefGoogle Scholar
Minsky, Y. N. and Taylor, S. J.. Fibered faces, veering triangulations, and the arc complex. Geom. Funct. Anal. 27(6) (2017), 1450–1496.10.1007/s00039-017-0430-yCrossRefGoogle Scholar
Oertel, U.. Incompressible branched surfaces. Invent. Math. 76(3) (1984), 385–410.10.1007/BF01388466CrossRefGoogle Scholar
Parlak, A.. Computation of the taut, the veering and the Teichmüller polynomials. Exp. Math. doi: https://doi.org/10.1080/10586458.2021.1985656. Published online 21 October 2021.CrossRefGoogle Scholar
Parlak, A.. The taut polynomial and the Alexander polynomial. Preprint, 2021, arXiv:2101.12162.Google Scholar
Parlak, A., Schleimer, S. and Segerman, H.. Veering, code for studying taut and veering ideal triangulations. GitHub, 2022, https://github.com/henryseg/Veering.Google Scholar
Schleimer, S. and Segerman, H.. From veering triangulations to link spaces and back again. Preprint, 2022, arXiv:1911.00006.Google Scholar
Schleimer, S. and Segerman, H.. Essential loops in taut ideal triangulations. Algebr. Geom. Topol. 20(1) (2020), 487–501.10.2140/agt.2020.20.487CrossRefGoogle Scholar
Strenner, B.. Fibrations of 3-manifolds and asymptotic translation length in the arc complex. Algebr. Geom. Topol., to appear.Google Scholar
Sun, H.. A transcendental invariant of pseudo-Anosov maps. J. Topol. 8(3) (2015), 711–743.10.1112/jtopol/jtv010CrossRefGoogle Scholar
Thurston, W. P.. A norm for the homology of 3-manifolds. Mem. Amer. Math. Soc. 59(339) (1986), 99–130.Google Scholar
Waldhausen, F.. On irreducible 3-manifolds which are sufficiently large. Ann. of Math. (2) 87(1) (1968), 56–88.10.2307/1970594CrossRefGoogle Scholar